
Past events
2026
02.02.2026 - Seminar: Alberto Chiarini(Università di Padova), Fluctuations of the Simple Exclusion Process on Point Processes14h00-15h00, Department of Mathematics, Aula Dal Passo.
Abstract
The simple exclusion process is one of the most prominent models of interacting particle systems. In this seminar, we consider a resistor network whose nodes are sampled according to a simple point process on R^d and are connected by certain conductances. On top of this resistor network, particles move according to random walks with the rule that there is at most one particle per site.
Under soft assumptions on the point process measure and conductances, which include ergodicity, stationarity and certain moment conditions, it is known that the empirical density of particles converges for almost all realisation of the environment to the solution of an heat equation with a certain homogenised diffusivity.
In this talk, we examine its equilibrium fluctuations. For d≥3, under the same assumptions that ensure the hydrodynamical limit, we show that the empirical density fluctuation field converges for almost all realisation of the environment, in the sense of finite-dimensional distributions, to a generalised Ornstein-Uhlenbeck process. For d=2, if we require some additional regularity on the environment to have Hölder regularity estimates for solutions to parabolic problems, we can show that the same conclusion holds.
07.01- 05.02.2026 - PhD Course: Lorenzo Dello Schiavo (Roma 2, Tor Vergata), Analytical Methods for Markov Processes
every Wednesday and Thursday, 14h15-16h00, Department of Mathematics, Aula Dal Passo.
Abstract
See HERE for the full abstract.
19.01.2026 - Seminar: Michele Stecconi (University Of Luxembourg), Universal cancellations in Uniform Random Waves
14h00-15h00, Department of Mathematics, Aula Dal Passo.
Abstract
I will present the model of "Uniform Random Waves", obtained by dividing a Gaussian random wave by its L2--norm, on the sphere and other Riemannian manifolds. This choice has deep motivations, although the Gaussian case predominates in the existing literature. I will compare the analysis of these two classes of random fields, focusing on (Wiener) chaos decomposition of geometric functionals and on new surprising (Berry) cancellation phenomena that arise in the uniform setting.
Based on the homonymous paper, with L. Gass, D. Marinucci, G. Peccati, F. Pistolato.
2025
01.12.2025 - Seminar: Giovanni Luca Torrisi (CNR), Posterior Bayesian Neural Networks with Dependent and Heavy-Tailed Weights14h00-15h00, Department of Mathematics, Aula Dal Passo.
Abstract
We consider fully connected and feedforward deep neural networks with dependent and possibly heavy-tailed weights. These networks have been introduced to alleviate the drawbacks due to a Gaussian initialization. In a Bayesian framework, when the likelihood is Gaussian, we identify the posterior distribution of the output in the sequential wide-width limit and, in the shallow case, we compute explicitly the posterior distribution of these models.
The talk is based on a joint work with Nicola Apollonio and Giovanni Franzina.
24.11.2025 - Seminar: Luisa Andreis (Università degli Studi di Torino), Large deviations for the covariance process in fully connected Gaussian neural networks
14h00-15h00, Department of Mathematics, Aula Dal Passo.
Abstract
In this talk, we study fully connected Gaussian deep neural networks, focusing on their covariance process. In particular, we establish a large deviation principle (LDP) for this process in a functional framework, viewing it as a trajectory in the space of continuous functions. As key applications of our main results, we derive posterior LDPs under Gaussian likelihoods in both the infinite-width and mean-field regimes. We will outline the main ideas of the proof, emphasizing that it relies on an LDP for the covariance process regarded as a Markov process taking values in the space of non-negative, symmetric, trace-class operators equipped with the trace norm.
This talk is based on joint work with F. Bassetti and C. Hirsch.
03.11.2025 - Seminar: Giorgio Cipolloni (Università di Roma, Tor Vergata), Logarithmically correlated fields from large random matrices
14h00-15h00, Department of Mathematics, Aula Dal Passo.
Abstract
We study the Brownian evolution of large non-Hermitian matrices and show that their log-determinant converges to a 2+1 dimensional Gaussian field in the Edwards-Wilkinson regularity class, i.e. logarithmically correlated for the parabolic distance. This gives a dynamical extension of the celebrated result by Rider and Virag (2006) proving that the fluctuations of the eigenvalues of Gaussian non-Hermitian matrices converge to the Gaussian Free Field.
05.11.2025 - Seminar: Milton Jara (IMPA, Rio de Janeiro), NESS for KPZ
16h00-17h00, Department of Mathematics, Aula D'Antoni.
Abstract
We show that the fluctuations of the density of boundary driven, weakly asymmetric systems are described by energy solutions of the KPZ equation with corresponding boundary conditions. Conditioned on the uniqueness of these energy solutions, we show that the non-equilibrium stationary states (NESS) of these systems are described by the invariant measures of KPZ introduced by Barraquand, Bryc, Corwin, Knizel among others.
Joint work with Juan Arroyave (IMPA).
07.11.2025 - Seminar: Maurice Duits (KTH Royal Institute of Technology, Stockholm), Integrable Structures Behind the Aztec Diamond
14h00-15h00, Department of Mathematics, Aula D'Antoni.
Abstract
The Aztec diamond, under the uniform measure on domino tilings, is one of the classic examples of an exactly solvable model in probability and statistical mechanics. Its rich geometric features—such as limit shapes and arctic boundaries—have long made it a cornerstone of integrable probability. More recently, variants of this model with doubly periodic weights have revealed that much of the underlying structure persists far beyond the uniform case and can be used to uncover new behaviors—such as regions with smooth disorder—that were previously out of reach. At the heart of these models lies a birational map that encodes their integrable character. In this talk, I will describe how this map unifies different regimes of the Aztec diamond—from uniform and periodic settings to models in random environments. I will also discuss how integrable features survive (sometimes unexpectedly) in the presence of disorder, and how they connect to other probabilistic models such as directed polymers. The presentation is aimed at a broad mathematical audience, and no prior background in tilings or integrable systems will be assumed.
06.10.2025 - Seminar: Federico Bassetti (Politecnico di Milano), Scaling Limits of Bayesian Neural Networks: Gaussian Processes and Mixtures
14h00-15h00, Department of Mathematics, Aula Dal Passo.
Abstract
In large neural networks, key theoretical insights emerge in the infinite-width limit, where the number of neurons per layer grows while depth stays fixed. In this regime, networks with Gaussian-initialized weights define a mixture of Gaussian processes with random covariance, which converges in the infinite-width limit to a pure Gaussian process with deterministic covariance. However, this Gaussian limit sacrifices descriptive power,
as it lacks the ability to learn dependent features and produce output correlations that reflect observed labels.
Motivated by these limitations, we explore deep linear networks in the proportional limit, where both depth and width diverge at a fixed ratio.
In this setting, the network converges to a nontrivial Gaussian mixture, both at the prior and posterior level.
This structure allows the network to capture dependencies in the outputs—an ability lost in the infinite-width limit but retained in finite networks.
Our contribution extends previous works by explicitly characterizing, for linear activation functions, the limiting distribution as a nontrivial mixture of Gaussians.
The talk is based on
F. Bassetti, L. Ladelli, P. Rotondo. Proportional infinite-width infinite-depth limit for deep linear neural networks (2024+) https://arxiv.org/abs/2411.15267
Bassetti,F. Gherardi, M. Ingrosso, A. Pastore, M. Rotondo, P. Feature learning in finite-width Bayesian deep linear networks with multiple outputs and convolutional layers.
Journal of Machine Learning Research 26 (2025) 1-35.
25.09.2025 - Workshop: A day on Random Matrix Theory and Deep Learning
09h30-17h00, Department of Mathematics, Aula Gismondi
Here the link to the webpage of the event.

07-11.04.2025 - Mini-course: Johannes Schmidt-Hieber (University of Twente), Statistical theory of deep learning
Department of Mathematics, Aula Dal Passo.
Schedule: Mon 14:00-16:30, Wed 14:00-16:30, Fri 14:00-16:30.
Teams streaming link
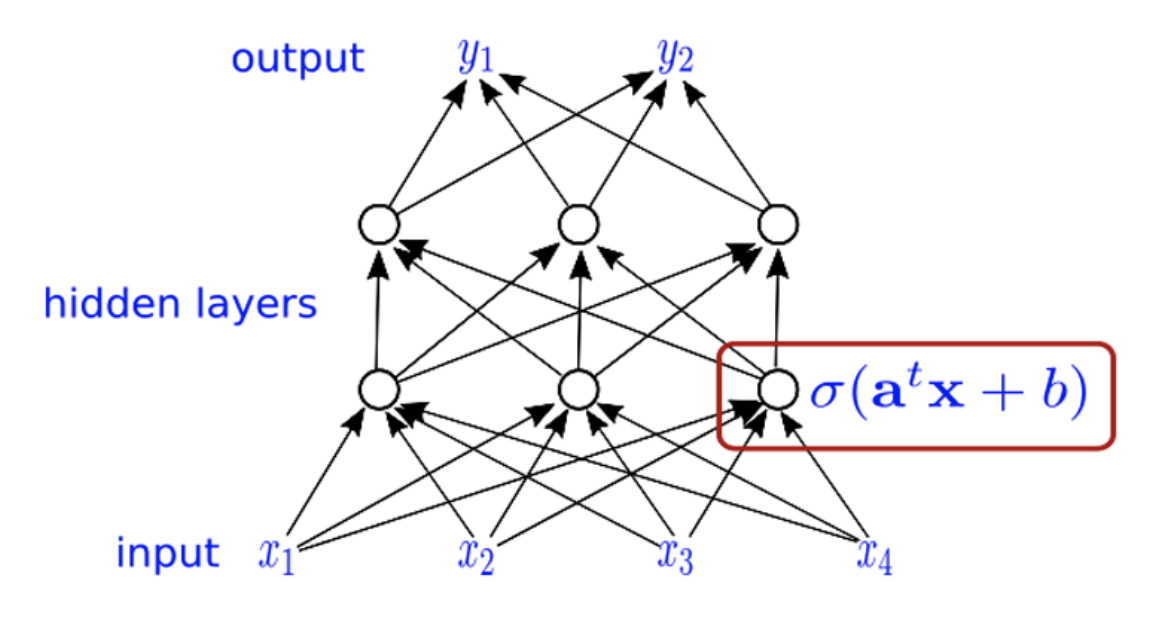
Abstract
Lecture 1. Intro and theory for shallow networks
- Perceptron convergence theorem
- Universal approximation theorem
- Approximation rates for shallow neural networks
- Barron spaces
- Advantages of additional hidden layers
- Deep ReLU networks
- Misclassification error for image deformation models
- Optimization in machine learning
- Weight balancing phenomenon
- Analysis of dropout
- Benign overfitting
- Grokking
31.03.2025 - Seminar/minimini-course: Francesco Preta (Stip AI, Berkeley), Basics of Natural Language Processing and applications of Large Language Models
14h00-17h00, Department of Mathematics, Aula Dal Passo.
Abstract
This seminar provides an introduction to Natural Language Processing (NLP), covering fundamental concepts such as tokenization, Named Entity Recognition (NER), and sentiment analysis. We will show how many NLP tasks can be translated into regular data science problem through the use of embeddings and introduce different embedding strategies for words and sentences obtained at different stages of history. Finally, we will explore the current industrial applications of Large Language Models (LLMs) including prompt engineering strategies, RAG and chatbots. Attendees will gain insights into how LLMs work, their advantages, and real-world use cases.
10.02.2025 - Double Seminar: Alexandre Stauffer (King's College London), Non-monotone phase transition in interacting particle systems
+ Jacopo Borga (MIT), Lattice Yang-Mills theory in the large N limit via sums over surfaces
14h00-16h00, Department of Mathematics, Aula Dal Passo.
Abstract Stauffer
In this talk we will discuss a reaction-diffusion particle system which has a non-monotone phase transition.
I will explain the techniques used to analyze monotone models and how they can be refined to
analyze non-monotone particle systems.
Based on upcoming works with Leandro Chiarini and Tom Finn.
Abstract Borga
Lattice Yang-Mills theories are important models in particle physics. They are defined on the d-dimensional lattice Z^d using a group of matrices of dimension N, and Wilson loop expectations are the fundamental observables of these theories. Recently, Cao, Park, and Sheffield showed that Wilson loop expectations can be expressed as sums over certain embedded bipartite maps of any genus. Building on this novel approach, we prove in the so-called strongly coupled regime:
- A rigorous formula in terms of embedded bipartite planar maps of Wilson loop expectations in the large N limit, in any dimension d.
- An exact computation of Wilson loop expectations in the large N limit, in dimension d=2, for a large family of (simple and non-simple) loops.
Previous results to the two aforementioned points were previously established by Chatterjee (2019) and Basu & Ganguly (2016), respectively. Our results extend these previous results, offer simpler proofs and provide a new perspective on these significant quantities.
This work is a collaboration with Sky Cao and Jasper Shogren-Knaak.
05.02.2025 - Seminar: Stefano Favaro (Università di Torino), A smoothed-Bayesian approach to frequency recovery from sketched data
14h00-15h00, Department of Mathematics, Aula Dal Passo.
Abstract
We introduce a novel statistical perspective on a classical problem at the intersection of computer science and information theory: recovering the empirical frequency of a symbol in a large discrete dataset using only a compressed representation, or sketch, obtained via random hashing. Departing from traditional algorithmic approaches, recent works have proposed Bayesian nonparametric (BNP) methods that can provide more informative frequency estimates by leveraging modeling assumptions on the distribution of the sketched data. In this paper, we propose a smoothed-Bayesian method, inspired by existing BNP approaches but designed in a frequentist framework to overcome the computational limitations of the BNP approaches when dealing with large-scale data from realistic distributions, including those with power-law tail behaviors. For sketches obtained with a single hash function, our approach is supported by frequentist guarantees, including unbiasedness and optimality under a squared error loss function within a class of linear estimators. For sketches with multiple hash functions, we introduce an approach based on multi-view learning to construct computationally efficient frequency estimators. We validate our method on synthetic and real data, comparing its performance to that of existing alternatives.
Joint work with Mario Beraha (Politecnico di Milano) and Matteo Sesia (University of Southern California)
2024
03.12.2024 - Seminar: Carlo Ciliberto (University College London), Operator World Models for Reinforcement Learning14h00-15h00, Department of Mathematics, Aula Dal Passo.
Abstract
Policy Mirror Descent (PMD) is a powerful and theoretically sound methodology for sequential decision making. However, it is not directly applicable to Reinforcement Learning (RL) due to the inaccessibility of explicit action-value functions. We address this challenge by introducing a novel approach based on learning a world model of the environment using conditional mean embeddings. Leveraging tools from operator theory we derive a closed-form expression of the action-value function in terms of the world model via simple matrix operations. Combining these estimators with PMD leads to POWR, a new RL algorithm for which we prove convergence rates to the global optimum. Preliminary experiments in finite and infinite state settings support the effectiveness of our method.
11-12-13.11.2024 - Course: Andrea Clementi, Luciano Gualà and Francesco Pasquale (Tor Vergata University), Mining Massive Data
, Department of Mathematics, Aula 1200.
Abstract
MONDAY, NOVEMBER 11, 14:15-18:00: Mining Huge Data Sets (Prof. Luciano Gualà)
TUESDAY, NOVEMBER 12, 14:15-18:00: WEB Search Engine (Prof. Andrea Clementi)
WEDNESDAY, NOVEMBER 13, 14:15-18:00: The Bitcoin Lightning Network (Prof. Francesco Pasquale)
31.10.2024 - Colloquium: Avi Wigderson (Princeton University), The Value of Errors in Proofs - The fascinating journey from Turing's 1936 R ≠ RE to the 2020 breakthrough of MIP* = RE
15h00-16h00, Department of Mathematics, Aula Gismondi.
Website of the event.
Abstract
In 2020, a group of theoretical computer scientists posted a paper on the Arxiv with the strange-looking title "MIP* = RE", impacting and surprising not only complexity theory but also some areas of math and physics. Specifically, it resolved, in the negative, the "Connes' embedding conjecture" in the area of von-Neumann algebras, and the "Tsirelson problem" in quantum information theory. You can find the paper here. As it happens, both acronyms MIP* and RE represent proof systems, of a very different nature. To explain them, we'll take a meandering journey through the classical and modern definitions of proof. I hope to explain how the methodology of computational complexity theory, especially modeling and classification (both problems and proofs) by algorithmic efficiency, naturally leads to the generation of new such notions and results (and more acronyms, like NP). A special focus will be on notions of proof which allow interaction, randomness, and errors, and their surprising power and magical properties, including ZK (Zero Knowledge proofs) and PCPs (Probababilistically Checkable Proofs). The talk will be non-technical, and requires no special background.
30.10.2024 - Lecture: Andrea Clementi and Francesco Pasquale (Tor Vergata University), Introduction to probabilistic checkable proofs and its applications in computer science (preparatory lecture to Avi Wigderson's seminar)
14h00-16h00, Department of Mathematics, Aula Dal Passo.
Abstract
We first shortly review the notions of decision problems and their computational complexity. We introduce the classes of decision problems P and NP: in particular, for NP, we use the notion of problems that are efficiently verifiable via a deterministic one-round proof protocol. According to the seminal works by Goldwasser et Al and Babai in the 80’s , we discuss the generalization of the NP proof system to Probabilistic Interactive Proofs (PIP). We then describe the two-rounds PIP protocol for the famous Graph Non-isomorphism Problem (GNIP) introduced by Goldwasser Micali & Wigderson that set an important question open for years. We then discuss some fundamental results and properties of PIP that globally revolutionize our view of the world of Computational Complexity Classes. In particular, we state the final result IP=PSPACE by Shamir (1990) showing that the class PSPACE of problems that can be solved in polynomial memory space coincides with the class of problems that admit an efficient PIP protocol. We give an informal description of the algebraic and probabilistic ingredients that play a crucial role in the proof of the above results.
After a brief overview of the consequences of IP protocols on the hardness of approximating NP-hard problems, such as min-coloring and max-clique in graphs, we move our attention to another relevant notion emerging from PIP: Zero-Knowledge (ZK) Proofs. i.e, proofs that yield nothing beyond the validity of the statement being proved. We present a few classical examples of ZK proofs and we hint at some recent applications in the context of modern cryptocurrencies.
16.10.2024 - Seminar: Alessandra Bianchi (University of Padova), Mixing cutoff for simple random walks on the Chung-Lu directed graph
14h00-15h00, Department of Mathematics, Aula D'Antoni.
Teams streaming link
Abstract
In this talk, we consider a simple random walk defined on a Chung-Lu directed graph, an inhomogeneous random network that extends the Erdos Renyi random digraph by including edges independently according to given Bernoulli laws. In this non-reversible setting, we will focus on the convergence toward the equilibrium of the dynamics. In particular, under the assumption that the average degree grows logarithmically in the size n of the graph (weakly dense regime), we will establish a cutoff phenomenon at the entropic time of order log(n)/loglog(n). We will then show that on a precise window the cutoff profile converges to the Gaussian tail function. This is qualitatively similar to what was proved in a series of works by Bordenave, Caputo, Salez for the directed configuration model, where degrees are deterministically fixed. In terms of statistical ensembles, this analysis provides an extension of these cutoff results from a hard to a soft-constrained model. Joint work with G. Passuello.
09.10.2024 - Seminar: Andriy Olenko (La Trobe University Melbourne), Limit theorems for multifractal products of random fields
14h00-15h00, Department of Mathematics, Aula Dal Passo.
Abstract
We will discuss the asymptotic properties of multifractal products of random fields. The obtained limit theorems provide conditions for the convergence of cumulative fields in $L_q$ spaces. New results concerning the rate of convergence of cumulative fields will also be presented. Simple, unified conditions for the limit theorems and the calculation of the Rényi function are provided, which are even less restrictive than those found in existing one-dimensional results. The developed methodology is further applied to multidimensional multifractal measures. Finally, a new class of examples based on geometric sub-Gaussian random fields will be introduced. In this case, the general assumptions take a simple form and can be expressed solely in terms of covariance functions. This presentation is based on joint work with I. Donhauzer (La Trobe University).
23-27.09.2024 - Summer school: High-Dimensional Approximation: From Theoretical Foundations to Machine Learning and PDEs, Cetraro, Italy.
Application deadline: May 15. All further information available at https://www.mat.uniroma2.it/~speleers/cime2024/.
Courses
Courses:
- Adaptivity in High-Dimensional Statistical Learning (Francis Bach)
- Numerics of High-Dimensional PDEs (Markus Bachmayr)
- High-Dimensional Approximation in Machine Learning (Gitta Kutyniok)
- High-Dimensional Integration (Dirk Nuyens)
- Compressive Sensing (Holger Rauhut)
17.06.2024 - Seminar: Tan Bui-Thanh (University of Texas at Austin), Learn2Solve: A Deep Learning Framework for Real-Time Solutions of Forward, Inverse, and UQ Problems
15h00-16h00, Department of Mathematics, Aula Dal Passo.
Abstract
Digital models (DMs) are designed to be replicas of systems and processes. At the core of a digital model (DM) is a physical/mathematical model that captures the behavior of the real system across temporal and spatial scales. One of the key roles of DMs is enabling “what if” scenario testing of hypothetical simulations to understand the implications at any point throughout the life cycle of the process, to monitor the process, to calibrate parameters to match the actual process and to quantify the uncertainties. In this talk, we will present various (faster than) real-time Scientific Deep Learning (SciDL) approaches for forward, inverse, and UQ problems. Both theoretical and numerical results for various problems including transport, heat, Burgers, (transonic and supersonic) Euler, and Navier-Stokes equations will be presented.
22.05.2024 - Seminar: Dario Trevisan (Università di Pisa), Gaussian Approximation and Bayesian Posterior Distribution in Random Deep Neural Networks
14h30-15h30, Department of Mathematics, Aula Dal Passo.
Link to Teams streaming.
Abstract
We establish novel rates for the Gaussian approximation of randomly initialized deep neural networks with Gaussian parameters and Lipschitz activation functions, in the so-called wide limit, i.e., where the sizes of all hidden layers become large. Using the Wasserstein metric and related functional analytic tools, we demonstrate the distribution of the output of a network and the corresponding Gaussian approximation are at a distance that scales inversely with the width of the network, surpassing previously established rates.
Furthermore, we extend our findings to approximate the exact Bayesian posterior distribution of the network when the likelihood is a bounded Lipschitz function of the network output, on a finite training set. This includes common cases, such as the Gaussian likelihood, which is defined as the exponential of the negative mean squared error. Our inequalities thus shed light on the network's Gaussian behavior by quantitatively capturing the distributional convergence results in the wide limit.
The exposition will aim to be self-contained, by introducing all the basic concepts related to artificial neural networks and Bayesian statistics to a mathematical audience. Based on arXiv:2203.07379 (joint with A. Basteri) and arXiv:2312.11737.
17.04.2024 - Seminar: Tommaso Rosati (University of Warwick), Lower bounds to Lyapunov exponents of stochastic PDEs
14h30-15h30, Department of Mathematics, Aula Dal Passo.
Abstract
Inspired by problems from fluid dynamics, we introduce an approach to obtain lower bounds to Lyapunov exponents of stochastic PDEs. Our proof relies on the introduction of a Lyapunov functional for the projective process associated to the equation, based on the study of dynamics of energy level sets and on a notion of non-degeneracy of the noise that leads to high-frequency stochastic instability. We address some nonlinear problems. Joint works with A. Blessing , M. Hairer, and (in progress) with M. Hairer, S. Punshon-Smith and J. Yi.
10.04.2024 - Seminar: Federico Camia (NYU Abu Dhabi), Towards a logarithmic conformal field theory of 2D critical percolation,
14h30-15h30, Department of Mathematics, Aula Dal Passo.
Abstract
Conformal field theory (CFT) provides a very powerful framework to study the large-scale properties of models of statistical mechanics at their critical point. The prototypical example of this is the continuum (scaling) limit of the two-dimensional critical Ising model. The case of critical percolation is more difficult, partly because its continuum limit is believed to be described by a relatively unusual type of CFT, called a logarithmic CFT. In this talk, I will first briefly explain the statements above. I will then present some recent results and work in progress that are part of a program aimed at fitting percolation within the logarithmic CFT framework.
27.03.2024 - Seminar: Quentin Berger (Sorbonne Université, Paris), Some results about the Ising model on a Galton-Watson tree
14h30-15h30, Department of Mathematics, Aula 1200.
Abstract
The goal of my talk is to present some results on the Ising model on a Galton-Watson tree. I will start with a general introduction, recalling in particular the seminal results of Russell Lyons. I will the present the results obtained in collaboration with Irene Ayuso Ventura (University Paris-Est Créteil), which estimate the effect of a sparse external field or boundary condition on the magnetisation of the root.
22.03.2024 - Seminar: Manisch Saga (Stanford University - Brain Dynamics Lab), Capturing brain dynamics using Topological Data Analysis
17h00-18h00, Department of Mathematics, Aula D'Antoni.
Abstract
Characterizing intrinsic and extrinsic transitions in cortical activity can provide an understanding of cognition, e.g., how the ebbs and flows of cognition are anchored in the transitions of neural activity. Further, such anchoring could , facilitate better models for psychiatric disorders and provide novel avenues for cognitive enhancement. This talk explores how noninvasive neuroimaging, despite its inherent limitations, can be leveraged to anchor cognitive performance and psychiatric nosology into rich spatiotemporal dynamics. We propose using tools from Topological Data Analysis (TDA), especially Mapper, to tackle the inherent noise in noninvasive neuroimaging devices and for capturing and characterizing brain dynamics in healthy and patient populations.
20.03.2024 - Seminar: Patrizio Frosini (Università di Bologna), Osservazioni geometriche per l'intelligenza artificiale
14h30-15h30, Department of Mathematics, Aula Dal Passo.
Abstract
In questo seminario verranno esposti, in un linguaggio non tecnico e non specialistico, alcuni contributi della geometria nella ricerca sull'apprendimento automatico e l'intelligenza artificiale. Inizieremo sottolineando l’importanza del concetto di osservatore per l’analisi dei dati e illustrando come tale concetto possa essere formalizzato tramite opportuni operatori, detti Group Equivariant Non-Expansive Operators (GENEO). Faremo vedere le principali conseguenze del modello matematico che utilizza i GENEO, orientato all’approssimazione degli osservatori piuttosto che all’approssimazione dei dati. Mostreremo come le proprietà di questo modello possano aprire la strada alla costruzione di strutture utili per il machine learning e la ricerca sull’intelligenza artificiale, passando attraverso la realizzazione di reti di GENEO. Concluderemo indicando alcune conseguenze dell'approccio operatoriale in rapporto all'interpretabilità e prevedibilità degli strumenti di apprendimento automatico.
15.03.2024 - Seminar: Maurizio Parton (Università di Chieti-Pescara), The simple and magical interplay of deep learning and reinforcement learning
14h00-15h00, Department of Mathematics, Aula D'Antoni.
Abstract
Reinforcement learning and deep learning are two completely different machine learning frameworks. Yet, they combine in a magical way to form deep reinforcement learning, which is the main driver of several of the recent breakthroughs in artificial intelligence, like game-playing AI, robotics, self-driving cars, advanced recommendation systems, chatbots, and beyond. I will give a concise overview of reinforcement learning and its magical interplay with deep learning. Questions are more than welcome, and for this reason I will keep the presentation under 30 minutes, maximizing time for discussion.
06.03.2024 - Seminar: Jodi Dianetti (Bielefeld University), Strong solutions to submodular mean field games with common noise and related McKean-Vlasov FBSDEs
14h30-15h30, Department of Mathematics, Aula Dal Passo.
Abstract
We study multidimensional mean field games with common noise and the related system of McKean-Vlasov forward-backward stochastic differential equations deriving from the stochastic maximum principle. We first propose some structural conditions which are related to the submodularity of the underlying mean field game and are a sort of opposite version of the well known Lasry-Lions monotonicity. By reformulating the representative player minimization problem via the stochastic maximum principle, the submodularity conditions allows to prove comparison principles for the forward-backward system, which correspond to the monotonicity of the best reply map. Building on this property, existence of strong solutions is shown via Tarski’s fixed point theorem, both for the mean field game and for the related McKean-Vlasov forward backward system. In both cases, the set of solutions enjoys a lattice structure with minimal and maximal solutions which can be approximated by the simple iteration of the best response map and by the Fictitious Play algorithm.
19-22.02.2024 - Mini-course: Giovanni Conforti (École Polytechnique, Paris) and Alain Durmus (École Polytechnique, Paris), An introduction to Score-based Generative Models
Mon 14h00-17h00, Wed 9h30-12h30, Thu 9:30-12:30, Department of Mathematics, Aula Dal Passo.
See here the syllabus of the course.
Registration of the lectures
Lecture 1 (Durmus) - Introduction to Generative Models - NOTE: In some parts of the video it is not possible to see what is written on the black board. Please refer to the Notes of Alain Durmus available here below!
Lecture 2 (Durmus) - Introduction to Score-based Generative Models
Lecture 3 (Conforti) - Score-based Diffusion Models
Lecture 4 (Conforti) - Diffusion Flow Matching
Material
Slides of Alain Durmus, Monday
Notes of Alain Durmus, Monday
Slides of Alain Durmus, Tuesday
Conforti Lecture notes
Abstract
In simple words, generative modeling consists in learning a map capable of generating new data instances that resemble a given set of observations, starting from a simple prior distribution, most often a standard Gaussian distribution. This course aims at providing a mathematical introduction to generative models and in particular to Score-based Generative Models (SGM). SGMs have gained prominence for their ability to generate realistic data across diverse domains, making them a popular tool for researchers and practitioners in machine learning. Participants will learn about the methodological and theoretical foundations, as well as some practical applications associated with these models. The first two lectures motivate the use of generative models, introduce their formalism and present two simple though relevant examples: energy-based models and Generative Adversarial Networks. In the third and fourth lecture we present score-based diffusion models and explain how they provide an algorithmical framework to the basic idea that sampling from the time-reversal of a diffusion process converts noise into new data instances. We shall do so following two different approaches: a first elementary one that only relies on discrete transition probabilities, and a second one based on stochastic calculus. After this introduction, we derive sharp theoretical guarantees of convergence for score-based diffusion models assembling together ideas coming from stochastic control, functional inequalities and regularity theory for Hamilton- Jacobi-Bellman equations. The course ends with an overview of some of the most recent and sophisticated algorithms such as flow matching and diffusion Sch¨odinger bridges (DSB), which bring an (entropic) optimal transport insight into generative modeling.

08.02.2024 - Seminar: Lorenzo Dello Schiavo (Institute of Science and Technology Austria), Conformally invariant random fields, quantum Liouville measures, and random Paneitz operators on Riemannian manifolds of even dimension
15h00-16h00, Department of Mathematics, Aula Dal Passo.
Abstract
On large classes of closed even-dimensional Riemannian manifolds M, we construct and study the Copolyharmonic Gaussian Field, i.e. a conformally invariant log-correlated Gaussian field of distributions on M. This random field is defined as the unique centered Gaussian field with covariance kernel given as the resolvent kernel of Graham—Jenne—Mason—Sparling (GJMS) operators of maximal order. The corresponding Gaussian Multiplicative Chaos is a generalization to the 2m-dimensional case of the celebrated Liouville Quantum Gravity measure in dimension two. We study the associated Liouville Brownian motion and random GJMS operator, the higher-dimensional analogues of the 2d Liouville Brownian Motion and of the random Laplacian. Finally, we study the Polyakov–Liouville measure on the space of distributions on M induced by the copolyharmonic Gaussian field, providing explicit conditions for its finiteness and computing the conformal anomaly. ( arXiv:2105.13925, joint work with Ronan Herry, Eva Kopfer, Karl-Theodor Sturm)
18.01.2024 - Seminar: Andrea Clementi (Tor Vergata), The Minority Dynamics and the Power of Synchronicity
15h45-16h45, Department of Mathematics, Aula Dal Passo.
Abstract
We study the minority-opinion dynamics over a fully-connected network of n nodes with binary opinions. Upon activation, a node receives a sample of opinions from a limited number of neighbors chosen uniformly at random. Each activated node then adopts the opinion that is least common within the received sample. Unlike all other known consensus dynamics, we prove that this elementary protocol behaves in dramatically different ways, depending on whether activations occur sequentially or in parallel. Specifically, we show that its expected consensus time is exponential in n under asynchronous models, such as asynchronous GOSSIP. On the other hand, despite its chaotic nature, we show that it converges within O(log^2 n) rounds with high probability under synchronous models, such as synchronous GOSSIP. Finally, our results shed light on the bit-dissemination problem, that was previously introduced to model the spread of information in biological scenarios. Specifically, our analysis implies that the minority-opinion dynamics is the first stateless solution to this problem, in the parallel passive-communication setting, achieving convergence within a polylogarithmic number of rounds. This, together with a known lower bound for sequential stateless dynamics, implies a parallel-vs-sequential gap for this problem that is nearly quadratic in the number n of nodes. This is in contrast to all known results for problems in this area, which exhibit a linear gap between the parallel and the sequential setting. Joint work with: L. Becchetti, F. Pasquale, L. Trevisan, R. Vacus, and I. Ziccardi The results will be presented at: ACM-SIAM Symposium on Discrete Algorithms (SODA24) Full version of the paper is available here: https://arxiv.org/abs/2310.13558
2023
07.12.2023 - Seminar: Matteo Quattropani (La Sapienza), Mixing of the Averaging process on graphs15h00-16h00, Department of Mathematics, Aula Dal Passo.
Abstract
The Averaging process (a.k.a. repeated averages) is a mass redistribution model over the vertex set of a graph. Given a graph G, the process starts with a non-negative mass associated to each vertex. The edges of G are equipped with Poissonian clocks: when an edge rings, the masses at the two extremes of the edge are equally redistributed on these two vertices. Clearly, as time grows to infinity, the state of the system will converge (in some sense) to a flat configuration in which all the vertices have the same mass. This very simple process has been introduced to the probabilistic community by Aldous and Lanoue in 2012. However, up to few years ago, there was no graph for which sharp quantitative results on the time needed to reach equilibrium were available. Indeed, the analysis of this process requires different tools compared to the classical Markov chain framework, and even in the case of seemingly straightforward geometries—such as the complete graph or the 1-d torus—it can be handled only by means of non trivial probabilistic and functional analytic techniques. During the talk, I’ll try to give a broad overview of the problem and of its difficulties, and I'll present the few examples that have been completely settled.
Based on joint work with P. Caputo (Roma Tre) and F. Sau (Università di Trieste)
02.11.2023 - Seminar: Adriano Barra (Università del Salento), A walk in the statistical mechanics of neural networks
15h00-16h00, Department of Mathematics, Aula Dal Passo. Link to Teams streaming.
Abstract
Purpose of this talk is twofold: in the first part, I will provide a statistical mechanical picture of shallow networks proving how learning in biological neural networks (e.g. in the Hopfield model) and standard machine learning via gradient descent (e.g. on the Boltzmann machine) ultimately convey the same information after training. This diminishes the gap in our understanding between biological and artificial information processing networks. In the second part of the talk, focusing on a toy model for the sake of simplicity, I will show how recent mathematical techniques, heavily based on Guerra's interpolation, are suitable to describe the emergent properties of this kind of networks.
26.10.2023 - Seminar: Emilio Cruciani (University of Salzburg), Dynamic algorithms for k-center on graphs
16h30-17h30, Aula 5 PP2.
Abstract
In this paper we give the first efficient algorithms for the k-center problem on dynamic graphs undergoing edge updates. In this problem, the goal is to partition the input into k sets by choosing k centers such that the maximum distance from any data point to the closest center is minimized. It is known that it is NP-hard to get a better than 2 approximation for this problem.
While in many applications the input may naturally be modeled as a graph, all prior works on k-center problem in dynamic settings are on metrics. In this paper, we give a deterministic decremental (2+ϵ)-approximation algorithm and a randomized incremental (4+ϵ)-approximation algorithm, both with amortized update time kno(1) for weighted graphs. Moreover, we show a reduction that leads to a fully dynamic (2+ϵ)-approximation algorithm for the k-center problem, with worst-case update time that is within a factor k of the state-of-the-art upper bound for maintaining (1+ϵ)-approximate single-source distances in graphs. Matching this bound is a natural goalpost because the approximate distances of each vertex to its center can be used to maintain a (2+ϵ)-approximation of the graph diameter and the fastest known algorithms for such a diameter approximation also rely on maintaining approximate single-source distances.
Joint work with: Sebastian Forster, Gramoz Goranci, Yasamin Nazari, Antonis Skarlatos
19.10.2023 - Seminar: Francesco D'Amore (Aalto University, Espoo), The Strong Lottery Ticket Hypothesis and the Random Subset Sum Problem, and Isabella Ziccardi (Bocconi) , Distributed Self-Stabilizing MIS Algorithms
14h00-16h00, Department of Mathematics, Aula Dal Passo.
Abstract D'Amore
The Strong Lottery Ticket Hypothesis (SLTH) posits that randomly-initialized neural networks contain subnetworks (strong lottery tickets) that achieve competitive accuracy when compared to sufficiently small target networks, even those that have been trained. Empirical evidence for this phenomenon was first observed by Ramanujan et al. in 2020, spurring a line of theoretical research: Malach et al. (2020), Pensia et al. (2020), da Cunha et al. (2022), and Burkholz (2022) have analytically proved formulations of the SLTH in various neural network classes and under different hypotheses.
In this presentation, we provide an overview of the state-of-the-art theoretical research on the SLTH and its connection with the Random Subset Sum (RSS) problem in theoretical computer science. While previous works on the SLTH ensure that the strong lottery ticket can be obtained via unstructured pruning, we demonstrate how recent advances in the multidimensional generalization of the RSS problem can be leveraged to obtain forms of structured pruning. Additionally, we highlight how refining the RSS results would yield tighter formulations of the SLTH.
This presentation is based on a joint work with Arthur da Cunha and Emanuele Natale that will be presented at NeurIPS 2023.
Abstract Ziccardi
I will discuss self-stabilizing distributed algorithms that find a Maximal Independent Set in an n-vertex graph. These algorithms share the feature of utilizing randomization to break symmetry. I will compare them based on the following parameters: the number of states used by each node, the knowledge of the graph required by each node, and their stabilization time. The first three algorithms are obtained by reconsidering some existing algorithms and making them self-stabilizing by introducing additional states. The first algorithm gets along with three states, but each node must have knowledge of ∆, the maximum node degree. In the second algorithm, nodes only need to be aware of their degree, but each node v has O(∆(v)) states, where ∆(v) is the degree of v. The third algorithm also requires O(∆(v)) states for each node v, but it works in the restricted beeping communication model. All three algorithms stabilize in O(log n) rounds with high probability. Lastly, I will talk about two algorithms that aim to create self-stabilizing algorithms with a constant number of states while requiring no knowledge of the underlying graph. The first algorithm is a natural process that, despite its simplicity, has received limited attention in the literature. It stabilizes in O(polylog(n)) rounds for specific graph families but may exhibit slower convergence time on general graphs. The final algorithm is a modification of this simple process, that tries to fix the particular situations that slow down the convergence.
12.10.2023 - Seminar: Guangqu Zheng (University of Liverpool), CLT and almost sure CLT for hyperbolic Anderson model with Lévy noise
15h00-16h00, Department of Mathematics, Aula Dal Passo
Abstract
In this talk, we will first briefly mention the recent research on CLT results of random field solutions to stochastic heat equations and stochastic wave equations with various Gaussian noises. Then, we will talk about the spatial ergodicity (first order result) and CLT (second order fluctuation) for a stochastic linear wave equation driven by Lévy noise, which is based on a joint work with R. Balan (Ottawa) [arXiv:2302.14178]. Finally, we will talk about the associated almost sure central limit theorem, based on a joint work with R. Balan (Ottawa) and P. Xia (Auburn).
25.09.2023 - Seminar: Marco Carfagnini (University of California San Diego), Spectral gaps via small deviations
15h00-16h00, Department of Mathematics, Aula Dal Passo. Link Teams.
Abstract
In this talk we will discuss spectral gaps of second order differential operators and their connection to limit laws such as small deviations and Chung’s laws of the iterated logarithm. The main focus is on hypoelliptic diffusions such as the Kolmogorov diffusion and horizontal Brownian motions on Carnot groups. If time permits, we will discuss spectral properties and existence of spectral gaps on general Dirichlet metric measure spaces.This talk is based on joint works with Maria (Masha) Gordina and Alexander (Sasha) Teplyaev.
15.09.2023 - Workshop: A day on Statistical Physics for Machine Learning
09h30-17h00, Department of Mathematics, Aula Gismondi
Here the link to the webpage of the event.

17.05.2023 - Seminar: Daniele Calandriello (Google Deep Mind, Paris), Efficient exploration in stochastic environments
Aula 2001.
Abstract
Machine learning has seen an explosive growth recently, driven mostly by breakthroughs in classification and generative models. However ML applications in decision making settings are much more limited, where data collection is much higher and ML models must be sufficiently robust and accurate to deal with unforeseen consequences and avoid worst case scenarios. In this talk we will introduce some classical results for online decision making in stochastic linear spaces, with applications to active learning, bandit/bayesian optimization and deep learning. Starting from a rigorous analysis of the noise propagation we can formulate provably robust (i.e. no-regret) algorithms, and then create variants that can scale to modern ML data regimes without sacrificing safety. And if time suffice, we will highlight how these approaches inspired a new wave of exploration techniques to enable reinforcement learning agents to solve extremely long horizon tasks.
24.05.2023 - Seminar: Rongfeng Sun (NUS, Singapore), A new correlation inequality for Ising models with external fields
Aula 2001, 14h00. Link to Teams
Abstract
We study ferromagnetic Ising models on finite graphs with an inhomogeneous external field. We show that the influence of boundary conditions on any given spin is maximised when the external field is identically 0. One corollary is that spin-spin correlation is maximised when the external field vanishes. In particular, the random field Ising model on Z^d, d ≥ 3, exhibits exponential decay of correlations in the entire high temperature regime of the pure Ising model. Another corollary is that the pure Ising model on Z^d, d ≥ 3, satisfies the conjectured strong spatial mixing property in the entire high temperature regime. Based on joint work with Jian Ding and Jian Song.
13.03-09.06.2023 - Course: Luciano Gualà (Università Tor Vergata), Advanced Topics on Algorithms
Mondays 16h00-18h00 (aula 3 PP2)
Wednesdays 16h00-18h00 (aula T7, Sogene).
See here all the details of the course.
26.04.2023 - Seminar: Federico Ricci Tersenghi (La Sapienza), Phase transitions and algorithmic thresholds for optimization and inference problems on sparse random graphs
Aula 2001, 14h00.
Abstract
Focusing on some fundamental constraint satisfaction problems defined on sparse random graphs (e.g. random k-sat, random q-coloring) I will start summarizing the rich phase diagram of the solution space which has been derived using powerful techniques from statistical mechanics of disordered systems. I will then discuss the implications of some of these phase transitions for the behaviour of smart algorithms searching for solutions. In the second part, I will consider the problem of inferring a signal from noisy and/or incomplete data within the Bayesian framework called the teacher-student scenario. I will discuss the corresponding phase diagrams and how phase transitions may affect the performances of inference algorithms based on message-passing and Monte Carlo sampling.
29.03.2023 - Seminar: Francesco Grotto (Università di Pisa), Random Waves, Oscillatory Integrals and Random Walks
Aula Dal Passo, 11h00.
Abstract
We consider Random Wave models, that is probability distributions on Laplacian eigenfunctions, on homogeneous spaces such as Euclidean spaces, Hyperspheres and Hyperbolic spaces. Determining the asymptotic behavior at large frequency of functionals of these objects is complicated by the oscillatory nature of their covariance functions. Oscillatory integrals appearing in evaluating variances of said functionals turn out to be closely related to integral representations of densities of uniform random walks in Euclidean spaces, and this connection can be exploited to deduce results on fluctuations of integral functionals of Random Waves.
15.02.2023 - Seminar: Francesco Vaccarino (Politecnico di Torino), Hodge-Shapley game: a Laplacian-based Shapley-like associated game for eXplainable AI
Aula Dal Passo, 14h00.
Abstract
In cooperative game theory, a set of players or decision-makers should negotiate to decide how to allocate the worth gained by the coalition composed of all the players. A value is a solution concept that suggests the outcome of the negotiation among players.
Among the many existing alternative solution concepts, it is prevalent the Shapley value solution concept. Its popularity also derives from the property of being a fair allocation, where a set of desirable properties or axioms describes fairness. The axioms characterize the Shapley value in the sense that it is the unique value satisfying those properties; at the same time, the axioms allow deriving a simple explicit combinatorial formula to compute the Shapley value.
In our approach, coalitions are the main subjects of cooperation, instead of single players, and, inspired by the Shapley value, the goal is to derive a fair associated game, i.e. an allocation to coalitions satisfying a set of desirable properties.
The methodology is based on using the Hodge decomposition of the simplicial complex associated with the partially ordered set of the subsets of the set of players ordered by inclusion. We will motivate this investigation within the framework of Explainable Artificial Intelligence (XAI).
Joint work with Antonio Mastropietro (Eurecom - F)
08.02.2023 - Seminar: Francesco Tudisco (Gran Sasso Science Institute), Efficient training of low-rank neural networks
Aula Dal Passo, 14h00. Slides.
Abstract
Neural networks have achieved tremendous success in a variety of applications. However, their memory footprint and computational demand can render them impractical in application settings with limited hardware or energy resources. At the same time, overparametrization seems to be necessary in order to overcome the highly nonconvex nature of the optimization problem. An optimal trade-off is then to be found in order to reduce networks' dimensions while maintaining high performance.
Popular approaches in the literature are based on pruning techniques that look for "winning tickets", smaller subnetworks achieving approximately the initial performance. However, these techniques are not able to reduce the memory footprint of the training phase and can be unstable with respect to the input weights. In this talk, we will present a training algorithm that looks for "low-rank lottery tickets" by interpreting the training phase as a continuous ODE and by integrating it within the manifold of low-rank matrices.
The low-rank subnetworks and their ranks are determined and adapted during the training phase, allowing the overall time and memory resources required by both training and inference phases to be reduced significantly.
We will illustrate the efficiency of this approach on a variety of fully connected and convolutional networks.
The talk is based on:
S Schotthöfer, E Zangrando, J Kusch, G Ceruti, F Tudisco
Low-rank lottery tickets: finding efficient low-rank neural networks via matrix differential equations
NeurIPS 2022
https://arxiv.org/pdf/2205.13571.pdf
01.02.2023 - Seminar: Giovanni Conforti (École Polytechnique, Paris), A probabilistic approach to exponential convergence of Sinkhorn's algorithm
Aula Dal Passo, 14h00. Slides.
Abstract
The entropic optimal transport problem (EOT) is obtained adding an entropic regularisation term in the cost function of the Monge-Kantorovich problem and is nowadays regularly employed in machine learning applications as a more tractable and numerically more stable version of the optimal transport problem. On the other hand, E.Schrödinger asked back in 1931 the question of finding the most likely evolution of a cloud of independent Brownian particles conditionally to observations. The mathematical formulation of his question through large deviations theory is known as the Schrödinger problem and turns out to be fully equivalent to EOT. In this talk, I shall illustrate both viewpoints and then move on to sketch the ideas of a probabilistic method to show exponential convergence of Sinkhorn's algorithm, whose application the heart of the recent successful applications of EOT in statistical machine learning and beyond. In particular, we shall discuss how the proposed method opens new perspective for showing exponential convergence for marginal distribution that are non compactly supported.
10-13.01.2023 - Mini-course: Boris Hanin (Princeton University), Neural Networks and Gaussian Processes
Aula Dal Passo, Tue 10th 14h00-16h00, Wed 11th 14h00-16h00, Fri 13th 10h00-12h00.
Video of Lecture 1.
Video of Lecture 2.
Video of Lecture 3.
Abstract
Lecture 1. Introduction to Neural Networks
- Definition and Examples
- Typical use of neural networks for supervised learning
- Big Questions: optimization, generalization with overparameterized interpolation, feature learning
- Gaussian process behavior at initialization
- NTK/linear dynamics in optimization
- Beyond the NTK/GP regime
- Higher order cumulants at initialization
- Tuning to criticality
- Open problems
2022
22-25.11.2022 - Mini-course: Dario Fasino and Enrico Bozzo (Università di Udine), Applicazioni dell'algebra lineare numerica allo studio di reti e sistemi complessiBiblioteca Storica, Tue 14h00-18h00, Wed 10h00-14h00, Thu 14h00-18h00. Download the slides from the first, second, third lecture of Enrico Bozzo. Download the slides from the first, second, third , fourth , fifth part of Dario Fasino's lecture.
Abstract
Enrico Bozzo: Sistemi dinamici lineari su grafi
Grafi e matrici: concetti di connettività, matrice di adiacenza,
matrici non negative, matrici primitive, teoria di Perron-Frobenius.
Matrici stocastiche e substocastiche, problema del consenso.
Matrici Laplaciane e di Metzler, punti di equilibrio e consenso nel caso continuo,
cenno ai sistemi compartimentali.
Dario Fasino: Metodi matriciali nell'analisi di reti complesse
Breve panoramica sulla scienza delle reti.
Concetti classici di centralità basati su cammini minimi.
Misure di centralità, somiglianza e distanza tra nodi basate su tecniche spettrali e funzioni di matrici.
Catene di Markov a tempo discreto: Percorsi casuali classici e non-retrocedenti.
Tecniche matriciali per la localizzazione di clusters, strutture core-periphery o quasi-bipartite.
Introduzione ai percorsi casuali del secondo ordine: Tensori stocastici, PageRank nonlineare.
15.12.2022 - Lecture: Andrea Clementi (Tor Vergata), Mining data streams
Aula 22, 16h30.
The lecture is intended for master and PhD students in Mathematics and Computer Science with no particular background on the subject. Here is a syllabus of the lecture.
16.11.2022 - Seminar: Cesare Molinari (IIT and Università di Genova), Iterative regularization for convex regularizers
Aula Dal Passo, 14h00. Slides.
Abstract
Iterative regularization exploits the implicit bias of an optimization algorithm to regularize ill-posed problems. Constructing algorithms with such built-in regularization mechanisms is a classic challenge in inverse problems but also in modern machine learning, where it provides both a new perspective on algorithms analysis, and significant speed-ups compared to explicit regularization. In this talk, we propose and study the first iterative regularization procedure able to handle biases described by non smooth and non strongly convex functionals, prominent in low-complexity regularization. Our approach is based on a primal-dual algorithm of which we analyze convergence and stability properties, even in the case where the original problem is unfeasible. The general results are illustrated considering the special case of sparse recovery with the ℓ1 penalty. Our theoretical results are complemented by experiments showing the computational benefits of our approach.
09.11.2022 - Seminar: Alessandra Cipriani (UCL), Topological data analysis: vineyards for metallic structures
Aula Dal Passo, 14h00. Slides.
Abstract
Modeling microstructures is a problem that interests material science as well as mathematics. The most basic model for steel microstructure is the Poisson-Voronoi diagram. It has mathematically attractive properties and has been used in the approximation of single-phase steel microstructures. We would like to present methods that can be used to assess whether a real microstructure can be approximated by such a model. In this talk, we construct tests that use data coming from serial sectioning (multiple 2D sections) of a 3D metallic structure. The proposed statistics exploit tools from topological data analysis such as persistence diagrams and (a modified version of) persistence vineyards.
02.11.2022 - Seminar: Guillaume Poly (University of Rennes 1), Around total variation for Breuer-Major Theorem and nodal volume of Gaussian fields
Aula Dal Passo, 14h00. Link to Teams.
Abstract
In this talk, i will revisit the Breuer-Major Theorem from the perspective of total variation metric and will introduce some known results recently established in this framework. I will then explain how to break the limitations of these results and establish unconditional criteria of convergence in total variation by using a specific gradient in Malliavin calculus (the sharp operator). Next, i will explain how this kind of ideas may be used in the framework of nodal volume of Gaussian fields in order to establish CLT in the total variation topology. This talk is mainly based on ongoing research with J.Angst and F.Dalmao.
26.10.2022 - Seminar: Solesne Bourguin (Boston University), Regularity of forward-backward SDEs via PDE techniques
Aula Dal Passo, 14h00.
Abstract
The study of the regularity of the law of solutions to SDEs is an important and classical topic in stochastic analysis. This was for instance Malliavin's motivation for the development of the stochastic calculus of variations in order to prove a probabilistic version of Hörmander's sum-of-squares theorem. The object of the present work is to study the regularity of solutions to forward-backward SDEs via a novel combination of the Malliavin calculus with PDE techniques such as backward uniqueness and strong unique continuation. We obtain new conditions for the existence of densities of solutions to backward SDEs that not only include all existing results as particular cases, but also allow us to deal with multidimensional forward components. Applications to finance and mathematical biology will be discussed if time permits.
15-16.09.2022 - Workshop: Topology of Data in Rome
Here the link to the webpage of the event.
List of speakers
Katherine Benjamin University of Oxford, UK
Ryan Budney University of Victoria, Canada
Wojtek Chacholski KTH, Sweden
Pawel Dłotko Dioscuri Centre of TDA, Poland
Barbara Giunti Graz University of Technology, Austria
Kelly Maggs École Politechnyque Fédérale de Lausanne, Switzerland
Anibal Medina Max Planck Institut für Mathematik, Germany
Bastian Rieck AIDOS Lab, Germany
02.09.2022 - Seminar: Elisa Alòs (Universitat Pompeu Fabra, Barcelona), On the skew and curvature of implied and local volatilities
Aula Dal Passo, 14h00.
Abstract
In this talk, we study the relationship between the short-end of the local and the implied volatility surfaces. Our results, based on Malliavin calculus techniques, recover the recent $\frac{1}{H+3/2}$ rule (where $H$ denotes the Hurst parameter of the volatility process) for rough volatilitites (see Bourgey, De Marco, Friz, and Pigato (2022)), that states that the short-time skew slope of the at-the-money implied volatility is $\frac{1}{H+3/2}$ the corresponding slope for local volatilities. Moreover, we see that the at-the-money short-end curvature of the implied volatility can be written in terms of the short-end skew and curvature of the local volatility and viceversa, and that this relationship depends on $H$.
13.06.2022 - Seminar: Davide Bianchi (Harbin Institute of Technology, Shenzhen), Asymptotic spectra of large graphs with a uniform local structure
Aula Dal Passo, 15h00.
Abstract
We are concerned with sequences of graphs with a uniform local structure. The underlying
sequence of adjacency matrices has a canonical eigenvalue distribution, in the Weyl sense, and
it has been shown that we can associate to it a symbol f, [2]. The knowledge of the symbol and
of its basic analytical features provides key information on the eigenvalue structure in terms of
localization, spectral gap, clustering, and global distribution.
We discuss different applications and provide numerical examples in order to underline the
practical use of the developed theory, [1]. In particular, we show how the knowledge of the
symbol f
• can benefit iterative methods to solve Poisson equations on large graphs;
• provides insight on the recurrence/transience property of random walks on graphs.
References
[1] A. Adriani, D. Bianchi, P. Ferrari, and S. Serra-Capizzano. Asymptotic spectra of large
(grid) graphs with a uniform local structure (part II): numerical applications. 2021. arXiv:
2111.13859.
[2] A. Adriani, D. Bianchi, and S. Serra-Capizzano. “Asymptotic spectra of large (grid) graphs
with a uniform local structure (part I): theory”. In: Milan Journal of Mathematics 88 (2020),
pp. 409–454.
11.05.2022-30.06.2022 - Course: Dmitri Koroliouk (Kiev), Introduction into Neural Networks and Deep Learning Download the program of the course. Links to the first lecture and second lecture.
02.05.2022-29.05.2022 - Course: Vlad Bally, Introduction to rough paths See the page of the course for schedule and abstract.
30.05.2022 - Conference: A Day on Random Graphs
Here the link to the webpage of the event.

Aula 1200, 14h00.
Giacomo Giorgio, Convergence in Total Variation for nonlinear functionals of random hyperspherical harmonics
Abstract
Random hyperspherical harmonics are Gaussian Laplace eigenfunctions on the unit d-dimensional sphere (d ≥ 2). We study the convergence in Total Variation distance for their nonlinear statistics in the high energy limit, i.e., for diverging sequences of Laplace eigenvalues. Our approach takes advantage of a recent result by Bally, Caramellino and Poly (2020): combining the Central Limit Theorem in Wasserstein distance obtained by Marinucci and Rossi (2015) for Hermite-rank 2 functionals with new results on the asymptotic behavior of their Malliavin-Sobolev norms, we are able to establish second order Gaussian fluctuations in this stronger probability metric as soon as the functional is regular enough. Our argument requires some novel estimates on moments of products of Gegenbauer polynomials that may be of independent interest, which we prove via the link between graph theory and diagram formulas.
Abstract
We present new high order approximations schemes for the Cox-Ingersoll-Ross (CIR) process that are obtained by using a recent technique developed by Alfonsi and Bally (2021) for the approximation of semigroups. The idea consists in using a suitable combination of discretization schemes calculated on different random grids to increase the order of convergence. This technique coupled with the second order scheme proposed by Alfonsi (2010) for the CIR leads to weak approximations of order $2k$ for all $k\in\N$. Despite the singularity of the square-root volatility coefficient, we show rigorously this order of convergence under some restrictions on the volatility parameters. We illustrate numerically the convergence of these approximations for the CIR process and for the Heston stochastic volatility model.
19.05.2022 - Lecture: Andrea Clementi, Finding Similar Items in Large Data Sets
Aula G2B, 11h00.
The lecture is intended for master and PhD students in Mathematics and Computer Science with no particular background on the subject. Here is a syllabus of the lecture.
09.05.2022 - Inauguration Colloquium: Lorenzo Rosasco (University of Genova), A guided tour of machine learning (theory)
Aula Dal Passo, 15h00. Slides of the seminar.
Bio of Lorenzo Rosasco
Lorenzo Rosasco is a professor at the University of Genova. He is also visiting professor at the Massachusetts Institute of Technology (MIT) and external collaborator at the Italian Technological Institute (IIT). He coordinates the Machine Learning Genova center (MaLGa) and leads the Laboratory for Computational and Statistical Learning focused on theory, algorithms and applications of machine learning. He received his PhD in 2006 from the University of Genova, after being a visiting student at the Center for Biological and Computational Learning at MIT, the Toyota Technological Institute at Chicago (TTI-Chicago) and the Johann Radon Institute for Computational and Applied Mathematics. Between 2006 a and 2013 he has been a postdoc and research scientist at the Brain and Cognitive Sciences Department at MIT. He his a recipient of a number of grants, including a FIRB and an ERC consolidator.
Abstract
In this talk, we will provide a basic introduction to some of the fundamental ideas and results in machine learning, with emphasis on mathematical aspects. We will begin contrasting the modern data driven approach to modeling to classic mechanistic approaches. Then, we will discuss basic elements of machine learning theory connected to approximation theory, probability and optimization. Finally, we will discuss the need of new theoretical advances at the light of recent empirical observations while using deep neural networks.

05.05.2022 - Seminar: Riccardo Maffucci (EPFL), Distribution of nodal intersections for random waves
Aula De Blasi, 16h00.
Abstract
This is work is collaboration with Maurizia Rossi. Random waves are Gaussian Laplacian eigenfunctions on the 3D torus. We investigate the length of intersection between the zero (nodal) set, and a fixed surface. Expectation, and variance in a general scenario are prior work. In the generic setting we prove a CLT. We will discuss (smaller order) variance and (non-Gaussian) limiting distribution in the case of ’static’ surfaces (e.g. sphere). Under a certain assumption, there is asymptotic full correlation between intersection length and nodal area.
29.04.2022 - Seminar: Antonio Lerario (Sissa), The zonoid algebra
Aula De Blasi, 14h00.
Abstract
In this seminar I will discuss the so called "zonoid algebra", a construction introduced in a recent work (joint with Breiding, Bürgisser and Mathis) which allows to put a ring structure on the set of zonoids (i.e. Hausdorff limits of Minkowski sums of segments). This framework gives a new perspective on classical objects in convex geometry, and it allows to introduce new functionals on zonoids, in particular generalizing the notion of mixed volume. Moreover this algebra plays the role of a probabilistic intersection ring for compact homogeneous spaces. Joint work with P. Breiding, P. Bürgisser and L. Mathis.
01.04.2022 - Seminar: Alessia Caponera, Nonparametric Estimation of Covariance and Autocovariance Operators on the Sphere
Aula 1200, 15h30.
Abstract
We propose nonparametric estimators for the second-order central moments of spherical random fields within a functional data context. We consider a measurement framework where each field among an identically distributed collection of spherical random fields is sampled at a few random directions, possibly subject to measurement error. The collection of fields could be i.i.d. or serially dependent. Though similar setups have already been explored for random functions defined on the unit interval, the nonparametric estimators proposed in the literature often rely on local polynomials, which do not readily extend to the (product) spherical setting. We therefore formulate our estimation procedure as a variational problem involving a generalized Tikhonov regularization term. The latter favours smooth covariance/autocovariance functions, where the smoothness is specified by means of suitable Sobolev-like pseudo-differential operators. Using the machinery of reproducing kernel Hilbert spaces, we establish representer theorems that fully characterize the form of our estimators. We determine their uniform rates of convergence as the number of fields diverges, both for the dense (increasing number of spatial samples) and sparse (bounded number of spatial samples) regimes. We moreover validate and demonstrate the practical feasibility of our estimation procedure in a simulation setting.
Authors: Alessia Caponera, Julien Fageot, Matthieu Simeoni and Victor M. Panaretos

