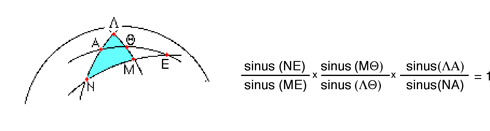|
Alcuni teoremi matematici, come altre espressioni del pensiero, seguono spesso la triste parabola che li vede per un certo periodo di gran moda per poi decadere nella più totale dimenticanza. Questo è il caso del teorema di Menelao, una volta essenziale per risolvere decisive questioni astronomiche, ora inutile dal momento che quelle questioni possono essere risolte facilmente con strumenti nuovi che fanno ricorso ai vettori nello spazio e alle operazioni che, tra essi, possono definirsi. Eppure, anche per un lettore moderno, il teorema di Menelao ha certamente un grande interesse per almeno due motivi. Il primo perchè lo lega alla nascita della trigonometria e in particolare spiega il motivo profondo che ha ha determinato l'abbandono dalla ben più naturale teoria delle corde, già sviluppata da Aristarco e poi da Tolomeo, per sostituirla con la teoria delle funzioni trigonometriche seno e coseno. Fatto di un certo rilievo , visto che la trigonometria viene oggi insegnata in tutte le scuole, senza probabilmente che si sappia il motivo che rende preferibile il considerare la mezza corda del doppio arco (cioè il seno di quell¹arco) anzichè la corda tout court.
Il secondo perchè si inserisce in un nuovo contesto geometrico, che per la prima volta e in modo consapevolee, sviluppa, per via assiomatica deduttiva, una geometria curva sulla scia della geometria euclidea, con i suoi angoli, triangoli ecc. che approderà, nel secolo XIX, alle così dette Geometrie non-euclidee. La contrapposizione Euclide-Menelao (o se si vuole piano-sfera) permette di evidenziare in modo semplice ed esplicito la relatività della geometria, spazzando via volumi e volumi di inutili speculazioni filosofiche e pseudo scientifche sul valore assoluto della geometria Euclidea.
Poiché è meno nota l'utilità applicativa della 'geometria curva' cominciamo col ricordarne l'interesse che essa aveva, tra gli scienziati alessandrini, nella descrizione scientifica degli astri e dei loro movimenti. Il punto di partenza consiste nel definire, in modo preciso, uno schema di riferimento capace di descrivere l'universo. Le stelle e tutti gli astri del cielo vengono proiettati sulla superficie di una grande sfera matematica (la volta celeste) il cui centro è occupato dall'osservatore. Le stelle vengono così a corrispondere a dei punti di questa teorica superficie. Il passo sucessivo, fondamentale, consiste nel definire l' allineamento di tre punti sulla sfera. La definizione è ovvia e naturale: tre stelle ci appaiano allineate quando i tre raggi con cui le vediamo stanno su uno stesso piano, cioè quando i tre corrispondenti punti della sfera si trovano su un piano che passa per il suo centro, o ancora, in termini più astratti, quando i tre punti si trovano su un cerchio massimo un cerchio cioè il cui raggio è il massimo possibile (uguale quindi a quello della sfera), e ciò accade quando il piano sul quale si trova questo cerchio passa per il centro della sfera. Ecco allora che risulta naturale e utile pensare alle stelle come ai punti di una sfera sulla quale le rette sono rappresentate da cerchi massimi e, come conseguenza di questo, sviluppare una nuova geometria a due dimensioni con i suoi segmenti, i suoi triangoli , angoli ecc, con gli stessi metodi che aveva usato Euclide per la geometria piana. Questo è il programma che sviluppa Menelao nel sua opera Sphaerica .
Nasce con questa opera lo studio della geometria curva che sarà poi ripresa e sviluppata solo alla fine del XVIII secolo da Gauss in tutta la sua generalità dando vita alla geometria intrinseca su una qualunque superficie curva (non solo il piano, come aveva fatto Euclide, o la sfera come aveva fatto Menelao) e quelle idee diventeranno poco dopo, con Riemann , i germi della moderna geometria differenziale dove la superficie (spazio a due sole dimensioni) viene sostituita da uno spazio curvo a tre o più dimensioni ancora, nel quale spazio Riemann indica come calcolare distanze, angoli, e come sviluppare la nuova geometria. Oggi queste idee sono ben lungi dall'essersi esaurite ed anzi hanno trovato un ampio spazio, a partire dalla teoria della relatività generale di Einstein, nella fisica teorica e rappresentano rami fruttuosi della ricerca matematica contemporanea.
In questo paragrafo tentiamo di illustrare uno dei teoremi principali della Sphaerica [Lib. III PROP. I. THEOR.] , noto come teorema di Menelao cercando di illustrare le coseguenze cui si accennava nella introduzione. Il teorema ha una versione piana, alcune volte chiamata col nome di regula sex quantitatum e una versione curva (sulla sfera) per l'appunto trattata da Menelao.
Regula sex quantitatum.
Se un triangolo 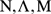 è tagliato da una trsversale non passante per i vertici, nei punti è tagliato da una trsversale non passante per i vertici, nei punti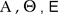 sui lati sui lati 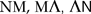 rispettivamente, allora il prodotto dei rapporti semplici costruiti sui tre lati è uno. Vale cioé la regola: rispettivamente, allora il prodotto dei rapporti semplici costruiti sui tre lati è uno. Vale cioé la regola:
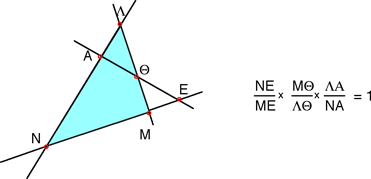
Ricordiamo che se tre punti A, B, P sono allineati, si chiama rapporto semplice dei tre punti il rapporto k tra la lunghezza del segmento AP con quella del segmento BP, o meglio lo scalare k che esprime il vettore geometrico AP come multiplo del vettore geometrico BP.
Di questo teorema esistono diverse dimostrazioni elementari la più semplice della quale si ottiene tracciando la retta parallela alla trasversale passante per il vertice N e ragionando sui triangoli simili che si vengono a costruire.
L'analogo risultato nella geometria della sfera, così come è riportato da Halley, recita testualmente:
Teorema di Menelao
Siano dati sulla superficie della sfera due archi di cerchio massimo 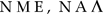 , internamente ai quali tracciamo altri due archi (di cerchio massimo) , internamente ai quali tracciamo altri due archi (di cerchio massimo) 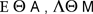 che si incontrano nel punto che si incontrano nel punto 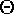 : dico che : dico che
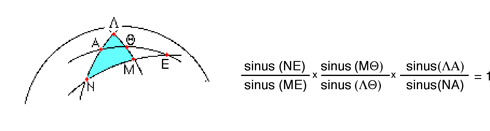
In questo enunciato appare per la prima volta la funzione sinus: ciò che modernamente intendiamo per seno trigonometrico di un angolo. In questo caso, quando scriviamo sinus(NE) l'angolo in esame, se O è il centro della sfera, è quello formato dalle semirette ON e OE (o, se la sfera è di raggio unitario, sinus(NE) significa il seno dell'arco NE misurato in radianti). L'etimologia della parola sinus (come lo stesso Halley ci avverte) è piuttosto complicata. Difatti la locuzione greca , che ritroviamo in Tolomeo e che probabilmente risale alla versione originale (andata perduta ) dell'opera di Menelao, usa per il seno di un angolo, la locuzione: ciò che è sotteso al doppio arco
cioè la corda sottesa dal doppio arco
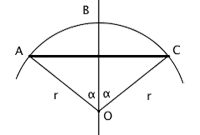
Più precisamente, il sotto del doppio di circonferenza AB è il sotto dell'arco AC cioè la corda AC. Dunque: il sotto del doppio di circonferenza AB coincide con 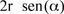 . .
Dopo la distruzione di Alessandria e della sua enorme biblioteca molte delle opere greche fortunosamente salvate dalla distruzione, tra cui certamente l'Almagest di Tolomeo, penetrarono nei circoli scientifici indiani e vennero da loro variamente rimaneggiate e riscritte in versi come le grandi epopee poetiche induiste. E' in quella visione poetica ed allegorica dove, richiamando l'immagine dell'arco e delle frecce, nascono i termini oggi di uso comune in matematica, quali appunto arco, corda ecc. riferiti alla geometria delle circonferenze. In particolare con la parola sanscrita jiva che significa corda di un arco si traduce la locuzione greca: ciò che è sotteso da un arco di circonferenza. Un problema nasceva però dal fatto che il teorema di Menelao e tutto ciò che da esso ne segue, stabilisce delle relazioni di proporzionalità non tanto tra le corde di un arco quanto, piuttosto, tra le corde del doppio arco, cioé tra i seni dell'arco. Poiché quindi questa espressione corda del doppio arco interveniva sempre nelle principali regole, fu coniato il termine abbreviato jya al posto della frase ardha jiva. Quando gli arabi intrappresero la traduzione dal sanscrito delle opere astronomiche indiane, non riuscirono a trovare nei loro dizionari, nessuna parola che significasse jya e così la tradussero con la parola jaib che aveva un suono simile ma anche un significato: nella lingua araba jaib, infatti significa cavità, tasca. Quando, infine, si arrivò a tradurre dall' arabo al latino, la parola jaib aveva assunto un ben preciso significato, fu tradotta col termine latino sinus che appunto vuol dire cavità.
La dimostrazione del Teorema di Menelao presuppone l'analogo teorema piano, la così detta regola delle sei quantità, di natura piùelementare che doveva essere ben nota, probabilmente allo stesso Euclide, e del quale Menelao non ne riportala neanche la dimostrazione.
Tolomeo invece nel suo Almagest (libro I capitolo 13), fa precedere la dimostrazione del teorema sferico con quella dell'analogo teorema piano ma inizia quel capitolo precisando immediatamente l'uso astronomico che si vuol fare del teorema di Menelao:
Il nostro prossimo obiettivo è quello di determinare il rapporto tra l'arco dell'equatore celeste, l'arco dell'eclittica e l'arco di cerchio massimo dal polo all'equatore
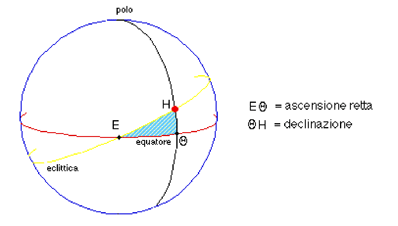 |
In altri termini, Tolomeo cerca una relazione tra i lati del triangolo sferico rettangolo che ha come cateti la declinazione e l¹ascensione retta e come ipotenusa un arco di eclittica.
|
La dimostrazione del teorema di Menelao che qua riportiamo è quella che si trova nella versione latina di Halley della Sphaerica ed è molto istruttiva perchè mostra come entra in scena, per la prima volta, la corda del doppio arco, questo nuovo importante personaggio della matematica, che a partire da questo teorema, assumerà un ruolo ben più importante della più semplice corda di un arco.
Dal teorema di Menelao è facile ricavare le formule di base per la trigonometria sferica.
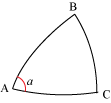 |
Se, ad esempio, consideriamo un triangolo sferico A,B,C rettangolo in C, detto a l'angolo sferico tra il cateto CA e
l'ipotenusa, BA, abbiamo la seguente formula risolutiva per i triangoli rettangoli
sen(BC)=sen(AB).sen(a)
|
La dimostrazione della formula risolutiva si ottiene facilmente, applicando il teorema di Menalao ad un opportuno triangolo sferico.
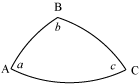
Notiamo che questa formula di geometria sferica, come il teorema di Menelao, sembra ottenersi dalla sua analoga, relativa alla geometria del piano, sostituendo le lunghezze dei segmenti con i seni trigonometrici degli archi corrispondenti. L'analogia riesce particolarmente chiara se si considera la geometria piana come il limite delle geometria sferica quando il raggio della sfera tende all'infinito. La cosa viene confermata dal teorema dei seni, che fornisce, per un qualunque triangolo sferico le analoghe relazioni.
 |
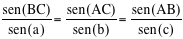
|
La prova del teorema dei seni si ottiene, come nel caso piano , tracciando le altezze e usando la formula risolutiva applicata ai triangoli rettangoli che in quel modo vengono generati.
Tolomeo, come abbiamo detto, usa la stessa formula risolutiva per i triangoli rettagoli, per calcolare la declinazione del Sole (cioè la sua altezza sull'orizzonte) sapendo l'angolo percorso sull'eclittica a partire dall'equinozio di primavera. Se quest'angolo è, ad esempio, di 30 gradi (cioè il Sole sta uscendo dalla costellazione dell'Ariete per entrare in quella del Toro), valutando come fa Tolomeo, l'nclinazione del piano dell'eclittica sul piano equatoriale di 23 gradi, 51 primi, la declinazione d del sole risulta data dalla relazione
sen(d)=sen(30o)sen(23o51')= 0,199
da cui d = 11o41'.
Calcoli analoghi permettono di trovare, per via teorica l'altezza del sole sull'orizzonte in ogni giorno dell'anno, valore che può essere facilmente misurato per verificare l'efficacia del modello.
E' dunque la formula risolutiva per i triangoli rettangoli che serve a Tolomeo per le sue applicazioni astronomiche e il caso vuole che questa stessa formula possa ottenersi diversamente senza alcun bisogno del non facile teorema di Menelao, usando proprietà di base del prodotto vettoriale . E' in questa seconda maniera, senz'altro più facile, che la formula viene presentata nei manuali moderni, così che del teorema di Menelao, diventato inutile, si perde traccia e con lui si perde anche la possibilità di una accurata ricostruzione della genesi di alcune idee basilari della matematica.
|

Menelao alessandrino
|