Il ragionamento è stato oggetto di studio della filosofia per secoli. L’imponente lavoro di Aristotele sulla logica e il lavoro di molti filosofi sull’argomento portano all’idea che il pensiero razionale è confacente alla potenzialità del pensiero umano La prima generazione di scienziati cognitivi ci ha decisamente descritto l’uomo come essere razionale. Bruner e Piaget, tanto per citare i più importanti, hanno scelto di lavorare su problemi che implicano la capacità degli uomini di ragionare in modo valido. Piaget ha supposto che gli esseri umani adulti ragionino applicando principi di logica, affermando :" Il ragionamento non è nient’altro che il calcolo proposizionale stesso "¹
Abbiamo già detto però che negli ultimi decenni le ricerche hanno evidenziato una sostanziale "irrazionalità"² nel ragionamento umano, che porta a difficoltà non trascurabili nel momento che si debbano concludere in modo esatto i sillogismi. Queste difficoltà emergono evidenti e con forza a tutti gli educatori, specialmente nel campo matematico, ed è uno scoglio che mette a dura prova le tecniche didattiche.

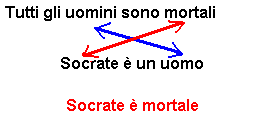
La persona comune in genere risolve bene sillogismi semplici con schema inferenziale del tipo modus ponens come il famosissimo

Tutti gli uomini sono mortali
Socrate è un uomo
Socrate è mortale

Notiamo che la conclusione corretta si raggiunge operando un "chiasma" tra le premesse che incrocia le associazioni

Ma spesso la natura associativa dei nostri processi di pensiero ci fa commettere errori persino in casi semplici come questa forma sillogistica, chiamata dalla scolastica medioevale "sillogismo in Barbara" Un errore classico è illustrato da questo sillogismo esposto in forma scherzosa da Bateson, che lo chiama "sillogismo in erba"³

L’erba è mortale
L’uomo è mortale
L’uomo è erba

Come si vede nella conclusione errata il chiasma è sacrificato alla spontanea associazione mortale-mortale => uomo-erba. Queste forme sono molto frequenti nella "logica" dei nostri alunni, (e ahimè, anche di molto adulti) che ignorano anche il giusto valore dei connettivi logici e dei quantificatori:

Alcuni delinquenti sono stranieri
Gli extracomunitari sono stranieri
Gli extracomunitari sono delinquenti

Oppure, ancora più sbrigativamente:

Nel quadrato (a + b)² è presente l’esponente 2
Nel binomio (a² + b²) è presente l’esponente 2
Il binomio è un quadrato

Le forme sillogistiche diventano veramente impegnative secondo i quantificatori impegnati nel sillogismo stesso. Vediamo ad esempio quali conclusioni possiamo trarre dalle seguenti premesse:

1. Tutti i banchieri sono atleti
   Nessun contabile è banchiere⁴



2. Tutti gli uomini imparziali sono giusti
   nessun uomo corrotto è giusto⁵



3. Tutti i francesi sono amanti del vino
   Alcuni amanti del vino sono buongustai⁶

Eulero ha dovuto superare difficoltà didattiche non indifferenti nel suo compito di precettore di matematica e fisica della principessa Anhalt-Dessau, nipote del re di Prussia. Nell’insegnarle principi di logica mise a punto una tecnica efficace, basata sull’aiuto che una rappresentazione visiva offre alla nostra limitata capacità di tenere contemporaneamente presenti alla mente molti elementi su cui operare. Parlando dei quattro tipi fondamentali di sillogismo Eulero scrive:

"Possiamo anche rappresentare con delle figure questi quattro tipi di proposizioni per esprimere visibilmente la loro natura alla vista. Questo è un aiuto meraviglioso per spiegare in modo veramente chiaro in cosa consista la correttezza di un ragionamento. Siccome una nozione generale racchiude una infinità di oggetti individuali, possiamo immaginarla come uno spazio nel quale tutti questi individui sono racchiusi: così per la nozione "uomo" si fa uno spazio, fig. 39, che si suppone contenga tutti gli uomini. Per la nozione di "mortatle" si fa un altro spazio, fig. 40, che si suppone contenga tutto ciò che è mortale. In seguito quando io dico "tutti gli uomini sono mortali", questo riviene a ciò che la prima figura è contenuta nella seconda"

L'immagine che segue, che è tratta dal libro di Eulero⁷ e che può essere ingrandita cliccandoci sopra, contiene le due figure citate.

Successivamente Eulero scrive:

"Queste figure tonde, o piuttosto questi spazi (perché non importa quale forma abbiano) sono molto utili per facilitare le nostre riflessioni su questa materia e farci scoprire tutti i misteri dei quali ci si vanta nella Logica e che si dimostrano a fatica, mentre, per mezzo di queste figure, tutto salta immediatamente agli occhi."

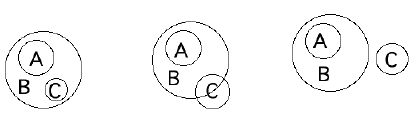
Possiamo costruire i diagrammi dei sillogismi presentati precedentemente, mettendo in evidenza la maggior facilità di arrivare alle giuste conclusioni "leggendole" nel diagramma. Gli schemi dei sillogismi precedenti sono i seguenti:

Possiamo vedere come, in quest’ultimo caso, le premesse non ci permettono di risolvere l’ambiguità riguardante l’intersezione tra A e C, che potrebbe o non potrebbe risultare vuota (per questo nulla ne discende).