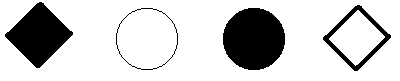Le nostre capacità inferenziali vengono messe a dura prova anche in una circostanza che richieda la capacità di ragionare su una regola disgiuntiva, insieme a quella di costruire ipotesi e valutarne le conseguenze. Parliamo in questo caso di ragionamento ipotetico-deduttivo.
Anche nell’analisi di questo problema si evidenzia il ruolo della rappresentazione mentale e quello del limite di capacità della memoria di lavoro. Il problema è stato inventato anch’esso da Wason¹, e prende il nome di "problema del THOG".

Eccone il testo:

Sono date quattro figure formate su due caratteristiche chiave: la forma geometrica e il colore: rombo, cerchio e bianco, nero. Si sceglie senza comunicarla una figura (data quindi da una forma e da un colore). Si chiamano THOG le figure che hanno o la forma o il colore della figura scelta, ma non ambedue insieme. Sapendo che il rombo nero è un THOG, quali, tra le figure rimanenti sono THOG?

La soluzione è in nota²

Il problema risulta risolto solo da una percentuale bassa dei soggetti, circa il 30%, e anche in questo caso una delle difficoltà sembra essere creata dai limiti della memoria a breve termine. ³

Non è questa la sede per approfondire l’argomento ma ne possiamo concludere che solo alcune operazioni logiche sono per noi naturali, mentre la logica nel suo complesso si impara solo studiando e allenandosi duramente. Il pensiero rigorosamente razionale non è affatto spontaneo, come lo è invece fare analogie e metafore, e per svilupparlo servono circostanze speciali, quali, per esempio, si incontrano nello studio della geometria razionale.
Questa era l’opinione, espressa nel 1877, di Giosuè Carducci e Francesco Rossetti riguardo al fine, nello studio secondario, che deve proporsi l’insegnamento della matematica.

... Tutti del resto per quel che spetta ai programmi ed ai libri di testo, si attengono alla legge: che se dovessimo consigliare il prof. Barsanti a riprendere il testo di Euclide, almeno per la materia contenuta nei primi libri, lo faremmo, perché noi crediamo che l'insegnamento liceale della matematica debba dare non dei matematici propriamente detti, ma piuttosto menti dallo studio matematico disciplinate e rafforzate al ragionamento, al quale scopo i libri d'Euclide furono giudicati meglio acconci⁴.

La seguente invece è l’opinione espressa nel 1936, di A. Einstein

D'altra parte intendo respingere l'idea che la scuola debba insegnare direttamente quelle conoscenze specializzate che si dovranno usare poi nella vita. Le esigenze della vita sono troppo molteplici perché appaia possibile un tale insegnamento specializzato nella scuola. La scuola dovrebbe sempre avere come suo fine che i giovani ne escano con personalità armoniose, non ridotti a specialisti. Lo sviluppo dell'attitudine generale a pensare e giudicare indipendentemente dovrebbe sempre essere al primo posto⁵.

Spiccano in tali opinioni l’attenzione per il carattere formativo della scuola. Evidentemente le menti disciplinate e rafforzate al ragionamento, l'attitudine generale a pensare e giudicare indipendentemente non erano, per chi parlava, prodotti garantiti dalla pratica quotidiana della vita, ma necessitavano di un adeguato allenamento e un’adeguata istruzione.
In questi ultimi decenni però dalle nostre scuole secondarie la geometria euclidea è quasi sparita e gli insegnamenti, sulla base di copiose indicazioni ministeriali, si sono spezzettati e moltiplicati cercando di coprire in modo specifico finalità pratiche ed esigenze della nostra vita quotidiana. L’insegnamento si deve prendere carico anche dei fondamentali aspetti formativi del pensiero, e le grandi riforme scolastiche dovrebbero salvaguardarli, nel momento in cui propongono nuovi assetti e contenuti.