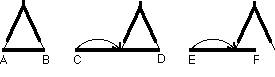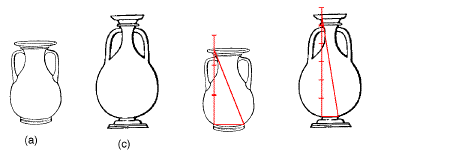|
Neuroscienze, apprendimento e didattica della matematica |
|
| 12. Il rapporto, il continuo, il
discreto |
||
| Di fronte al nume è infante l’uomo, come di fronte all’uomo il fanciullo ERACLITO |
L’idea di logos è veramente
ricca di significati che via via si sono stabilizzati intorno al concetto di
rapporto, di discorso, di ragionamento. In Eraclito troviamo: è dell’anima un logos che accresce se
stesso dove, in questo caso1 logos sembra voler dire "tensione
"espressiva" e tale tensione espressiva si manifesta nella
tendenza propria dell’anima a moltiplicare le proprie assonanze ed
immagini, in una progressione pressoché infinita, secondo un
inesausto ritmo generativo di mondi. Il logos e’ per la scuola di Pitagora il
fondamento per la comprensione del mondo: I Pitagorici affermano che [criterio di verità]
sia il, non inteso nel significato generale, ma in quello che deriva dalle
scienze matematiche - come appunto diceva Filolao - e che, essendo legato
alla percezione mentale della natura del tutto, abbia con essa una certa
affinità, se è vero come è vero, che il simile viene
compreso naturalmente dal simile2
L'uso dello stesso termine, logos, per indicare
rapporto in senso matematico e argomentazione razionale è molto
suggestivo e porta ad aggiungere profondità e spessore al pensiero
pitagorico. Il rapporto A:B sembra essere visto come un movimento di
pensiero, come una qualche costruzione rigorosa, quantitativa che lega A
a B, che permette di dedurre B da A come una
qualunque altra forma di ragionamento. Il costituirsi di un rapporto permette di dare alla
descrizione delle entità in gioco un valore di "verità" pari
a quello che il ragionare astratto avrebbe raggiunto, con Aristotele,
attraverso sillogismi ben formati. L'identità del termine , tra
rapporto e ragione, toglie dunque al rapporto il solo connotato numerico e
gli conferisce la dignità di pensiero, di un pensiero che si muove e
porta a individuare forme, somiglianze, leggi, principi
universali3
| Il logos nella scuola pitagorica |
In Euclide il concetto viene definitivamente formalizzato
riducendone anche, in parte, l’originaria generalità. Rapporto tra due grandezze omogenee e’ un certo
modo di comportarsi rispetto alla quantità In questa definizione, molto criticata perché
ritenuta tautologica, si dichiara che può esistere un rapporto solo
tra grandezze omogenee e che questo rapporto ha a che fare con una qualche
quantità. Si dice che hanno tra loro rapporto le grandezze le
quali possono, se moltiplicate, superarsi reciprocamente4 Ora Euclide esplicitamente chiede che gli enti coi quali
si vuole stabilire un rapporto verifichino due proprietà
fondamentali: (a) gli enti debbono potersi confrontare, comparare tra
loro in modo che si possa stabilire univocamente se A e’ o no
più "grande" di B. Si chiede quindi, come si dice
oggi, che gli enti coi quali si vuole stabilire un rapporto, formino un
insieme totalmente ordinato. Quest’interpretazione dà un
significato preciso al termine "superarsi". (b) data una entità A deve essere possibile
costruire 2A, 3A, 4A ecc., in modo tale che, date due
qualunque entità A e B si possano sempre trovare interi
positivi n e m tali che nA > B e
mB > A. Questa proprietà e’ nota oggi come postulato
di Archimede. | Il rapporto in Euclide | |
Archimede infatti, nell’Arenario, dimostra che dato
un granello di sabbia e l’intero universo esiste un numero intero n di
granelli di sabbia, che lui calcola esplicitamente, talmente grande da
formare un volume più grande di quello dell’intero universo (che
suppone una sfera di raggio finito). Questo postulato e’ descritto in modo molto efficace
da Guedj. E’ la descrizione di una lezione di matematica e
dell’impressione che questa fece sul ragazzo che la stava ascoltando e
che ora, da vecchio, la racconta: "Ricordo quasi parola per parola quello che disse
l’insegnante: "esiste sempre un multiplo del più piccolo
che e’ superiore al più grande". Lì per lì,
non abbiamo capito niente. Allora ce lo ha spiegato: "avendo un
segmento piccolo e uno grande, e’ sempre possibile, moltiplicando
quello piccolo, superare quello grande" Nella mia testa ci fu come
un’esplosione. Subito dopo suonò la campana. Avrei voluto
parlare all’insegnante, ma lui aveva fretta. Nel tornare a casa mi sono
seduto su dei ruderi e ho riflettuto per la prima volta in vita mia, lo
avevo già fatto, voglio dire, ma involontariamente, mentre quella
volta mi sono imposto di riflettere. Mi sono detto : "Ottavio il
segmento piccolo sei tu" E tutto mi e’ parso chiaro.
L’insegnate aveva ripetuto le parole di Archimede: "Per quanto tu
possa essere un segmento piccolo, puoi sempre moltiplicarti e diventare
più grande di qualunque altro segmento, di qualsiasi
grandezza"5 Questo modo di proporre il postulato di Archimede gli
conferisce molto più significato che non il modo astratto che abbiamo
riferito sopra. Già l’uso di segmenti invece che di grandezze
astratte, l’uso dei termini "piccolo" e "grande",
del termine "superare", fornisce immediatamente, nella mente di
chi ascolta, delle immagini mentali in grado di dare significato, forma,
stabilità al concetto che si vuole esprimere. | Il postulato di Archimede | |
Naturalmente i postulati (a) e (b) sono formulati col
loro corredo di proprietà formali (tipo nA+nB = n(A+B) che ne garantiscono l’uso standard6 . Un primo esempio, ovvio, di entità che verificano
questi postulati, sono i numeri interi. Un altro e’ dato dai segmenti:
ha infatti senso dire che il segmento A e’ "piu’
grande" del segmento B, intendendo con questo che A
e’ più lungo di B; il postulato archimedeo e’
ovviamente verificato. | L’analogia tra numero ed estensione |
|
| Tutte le cose al numero consentono PITAGORA |
Le vibrazioni di due corde sottoposte alla stessa tensione, ma di lunghezze
diverse, producevano, pizzicate insieme, un suono gradevole solo quando il
rapporto tra le loro lunghezze era come 1 con 2 (accordo di ottava) o 2 con
3 (accordo di quinta) o 3 con 4 (accordo di quarta) e così via. Non
contava la "misura" effettiva delle corde, ma il loro rapporto e
cioè il fatto che una fosse il doppio dell’altra, o che fosse
tre volte la metà dell’altra ecc. Questa misura poteva essere
una lunghezza, o anche un volume (quello del martello che pare Pitagora
abbia ascoltato nella bottega del fabbro) o la tensione provocata da pesi
diversi su corde della medesima lunghezza. Quello che contava insomma era
il logos che legava le due corde tra loro, come 1 con 2 o come 2 con
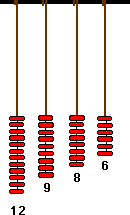
3! [Pitagora] passò davanti all’officina di un fabbro e, per sorte in un certo senso divina, ebbe a udire dei martelli che battevano il ferro sull’incudine e davano suoni tutti in perfetto accordo armonico reciproco, tranne una coppia. In quei suoni Pitagora riconosceva gli accordi di ottava, di quinta e di quarta, e notava che l’intervallo di quarta e quinta era di se stesso dissonante, ma idoneo a colmare la differenza di grandezza intercorrente tra l’una e l’altra. Lieto che con l’aiuto divino il suo intento venisse a realizzarsi, entrò nell’officina e grazie a svariate prove capì che la differenza nell’altezza dei suoni dipendeva dal peso dei martelli e non dalla forza con cui si batteva, ne’ dalla forma dei martelli medesimi, ne’ dalla posizione del ferro battuto. Poi dopo aver fissato con la medesima precisione il peso dei martelli, se ne tornò a casa. Qui fissò all’angolo di due pareti un unico piolo... e al piolo legò una dopo l’altra quattro corde di eguale spessore e tensione, fatte dalla stesa materia e dallo stesso numero di fili, e all’estremità inferiore di esse legò un peso, badando che le corde fossero di lunghezza perfettamente uguale. Quindi pizzicando le corde a due a due alternativamente trovava gli accordi già menzionati, uno per ogni coppia di corde. In effetti capì che la corda tesa col peso più grande risuonava di un rapporto di ottava con quella tesa col peso più piccolo: una aveva un peso di 12 unità e l’altra di 6. Così dimostrava che l’ottava si basa sul rapporto 2 con 1 come indicavano gli stessi pesi. La corda con il peso più grande risuonava in un accordo di quinta con quella che aveva otto unità di peso ed era posta accanto alla corda tesa col peso più piccolo: su questa base dimostrò che la quinta e’ basata sul rapporto di 3 con 2, lo stesso nel quale stavano i pesi...7
Pesi, velocità, aree , volumi, intensità luminosa, grandezza d’animo, senso di giustizia, tutto poteva essere rapportato trattato astrattamente sulla base di una qualche "misura" che ne evidenziasse la caratteristica, la "grandezza" da prendere in esame. Il segmento, a cui e’ associata la sua lunghezza, diventa il paradigma universale, l’esempio portante, la geometrizzazione di tutta la teoria. Il segmento e’ immediatamente visibile e la sua lunghezza immediatamente confrontabile con quella degli altri segmenti senza bisogno di un "metro" che ne misuri in un qualche modo il valore. In questo modo l’immagine visiva della "grandezza" , qualunque cosa essa sia, diventa un segmento e questo fornirà degli efficaci isomorfismi mentali in grado di guidare l’intuizione e la sua interazione con le costruzioni logico- formali. Se da un lato dunque l’analogia tra grandezze, rapporti tra grandezze e numeri interi apriva a una nuova visione del mondo, d’altro lato profonde differenze e difficoltà anche sul piano concettuale rendevano a volte impossibile una totale identificazione dei due mondi. Se l’aritmetica e la geometria parevano unificarsi nel pensiero pitagorico, nello stesso tempo l’approfondimento dei concetti a cui quel pensiero portava, creerà per la prima volta e solo nella nostra cultura occidentale, la consapevolezza di un incolmabile fossato che separa il discreto dal continuo, il numero (qui e nel seguito da intendersi come numero naturale) dalla forma | La scoperta dell’armonia musicale |
"Nel principio Iddio creò i cieli e la terra. E
la terra era informe e vuota, e le tenebre coprivano la faccia
dell’abisso e lo spirito di Dio aleggiava sulla superficie delle acque.
E Dio disse: "Sia la luce!" E la luce fu. .. e Dio separò
la luce dalle tenebre....Così fu sera, poi fu mattina: e fu il primo
giorno. Poi Dio disse: "Ci sia una distesa tra le acque che separi le
acque dalle acque". E Dio fece la distesa e separò le acque
ch’erano sotto la distesa dalle acque ch’erano sopra la distesa. E
così fu..... Così fu sera, poi fu mattina, e fu il secondo
giorno." Questo passo della Genesi è molto bello: da un
solo gesto di divisione nascono improvvisi il concetto di tempo -
così fu sera e poi mattina - e il concetto di grandezza di dimensione
- la distesa - il sopra, il sotto. Il tempo e lo spazio. Sono categorie
fondamentali per la nostra mente e certamente chi narrava "sapeva" in
qualche modo che dovevano essere al principio di ogni altra cosa. ".... Chiunque si tuffi nell'infinito, sia nel tempo
che nello spazio, senza interrompersi ha bisogno di punti fissi, di pietre
miliari perché altrimenti il suo movimento non sarebbe distinguibile
dall’immobilità'. Devono esserci stelle oltre le quali
sfrecciare, segnali dai quali egli possa misurare la distanza che ha
traversato. Egli deve dividere l'universo in distanze di una data lunghezza,
in compartimenti che ricorrano in una serie interminabile. Ogni volta che
egli supera un confine tra un compartimento e l'altro, il suo orologio fa
tic....."8 Il suo orologio fa tic. Nella Genesi i sei giorni della
creazione rotolano in un silenzio assoluto, senza nessun accenno a suoni o
rumori, ma già quel ritmo interno alle cose scuote l’infinito e
lo rende in qualche modo accessibile ai movimenti del corpo e della mente.
Perché la nostra mente ha bisogno di creare configurazioni stabili
nel caos indistinto di informazioni che riceve dalle percezioni del mondo
esterno, ed è strutturata proprio per farlo. Così gli stimoli
percettivi si organizzano secondo leggi permanenti e creano forme che
costruiscono pensieri e azioni. Il ritmo e la misura. La misura e il tempo.
Come nasce la misura? Basta una volta.... una volta nel tempo e una volta
nello spazio. | Numeri e grandezze | |
E’ stata in effetti osservata una rottura nella scala numerica
intorno al quattro. Esperimenti condotti da più ricercatori12 hanno evidenziato come i processi di valutazione
numerica di un certo numero di oggetti siano completamente diversi per
numeri maggiori o minori di quattro. In questo ultimo caso infatti la
valutazione viene effettuata con un processo di valutazione percettiva
immediata, globale, di "stima" , mentre per numeri più
grandi è necessario un conteggio vero e proprio. Si spiegherebbe in
questo modo13 il fatto che il segno dell’unità è
ripetuto, nelle scritture antiche, fino al massimo di quattro volte
(pensiamo per esempio alle cifre romane). Serie di segni più lunghe
risulterebbero illeggibili in una visione immediata e costringerebbero a un
conteggio sequenziale, rendendo lenta e difficile la lettura. Per i numeri
più grandi, o viene introdotto un nuovo simbolo, oppure i segni
unitari vengono organizzati in due o più gruppi, in modo che si
possano di nuovo stimare in un sol colpo d’occhio14 . | Processi cerebrali di valutazione numerica |
|
Consideriamo un qualunque insieme formato da diversi
oggetti. Esistono in matematica due concetti che evidenziano processi e modi
diversi di elaborazione del pensiero di fronte a quello stesso stimolo: la
cardinalità e l’ordinalità. Nella conversazione sono utilizzate forme esclamative,
per esempio nelle discussioni fra uomini al ritorno dalla caccia : "Uno solo
io ho ucciso - due io - tre io - quattro io - cinque io...." Questo popolo non riesce ancora a slegare il numero dal
processo cerebrale che lo elabora e che lo nomina, elaborazione che si
svolge sequenzialmente Nell’esporre il risultato della caccia si
ripercorre dall’uno al cinque le tappe che si sono succedute.
C’è una reale difficoltà a ricostruire una
quantità in modi che non passino attraverso il susseguirsi ritmico
del contare e a realizzare che è sufficiente un solo termine, il
cinque, per esprimere la quantità effettiva. | Numeri ordinali e numeri cardinali |
|
Si capisce attraverso questi esempi come possa nascere un
intrecciarsi di questi due piani, quello della percezione dell’essenza
di una quantità, di una grandezza, di una estensione e quello invece
che pone l’accento su ogni elemento che costituisce l’oggetto e lo
lega agli altri solo con un operazione di ordinamento. La dominanza stretta
di un processo di pensiero su un altro lascia posto a uno scambio di
informazioni e a una collaborazione nella costruzione di simboli usando dati
provenienti da funzioni mentali diverse e nella loro elaborazione. Questo
intreccio non deve però farci dimenticare le matrici multiple del
nostro pensiero, che restano separate e diverse nelle considerazioni e nei
singoli prodotti. Consideriamo la figura seguente: Certamente l’oggetto sulla sinistra viene percepito
come una unità, mentre quello sulla destra viene visto come una
pluralità. Cosa conferisce queste caratteristiche ai due disegni?
Forse il fatto che identifichiamo quello a sinistra come un rettangolo e non
come quattro segmenti con estremi in comune, e neanche come due parti di
piano, una interna e una esterna alla linea chiusa, mentre vediamo quello a
destra come un susseguirsi di punti separati, anche se legati da una
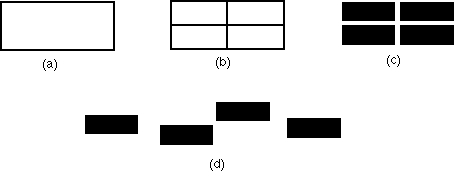
vicinanza e quindi da una sorta di destino comune. Nel caso
seguente: l’unità è più difficile da
definire. Sicuramente il caso (a) la rappresenta e il caso (d) no, ma nelle
situazioni intermedie l'occhio è incerto. Mi sembra di poter
affermare che il caso (b) sia ancora percepito come una unità, della
quale si può stabilire anche una cardinalità, 4, (non comincia
ad essere contraddittorio tutto ciò?) e il caso (c) presenti una
ambiguità di lettura: una bandiera per esempio (cioè una
figura chiusa), o quattro rettangoli molto vicini? "Numero è una pluralità composta di
unità"16 Non definisce invece l’unità tra le grandezze
nel libro V dedicato ai rapporti . Non ha senso o importanza per lui
definire la grandezza unitaria. Lo strumento necessario per trattare le
grandezze è la comparazione: Una grandezza è parte di una grandezza, la
minore di quella maggiore, quando essa misuri la maggiore.
La grandezza maggiore è multipla di quella minore,
quando sia misurata dalla minore.17 La comparazione permette di confrontare due grandezze e
di stabilire quante volte una di loro entra nell’altra. "Volta".
Rientra in gioco questo movimento del pensiero, e in questo caso suo
strumento non può che essere il compasso. In questo modo sia AB che CD che EF sono "uno" ma nel
loro compararsi AB diventa unità rispetto a CD, mentre non lo
è rispetto a EF. L’unità così, tra le grandezze,
non è più un concetto assoluto come nei numeri, dove
l’uno è tanto assoluto da diventarne l’unica radice pur
stando fuori di essi. U è parte di AB. E’ una qualunque
delle parti in cui divide AB, e viene chiamato, in questo caso "settimo". Ed
è chiaro che in questo termine si perde completamente il senso di
ordine, che acquista se lo usiamo nel movimento del conteggio. Il "settimo"
U è nato da una comparazione e dalla stima di una
cardinalità. Il segmento V invece, non è parte di AB,
secondo la definizione euclidea, così come ST non è parte di
CD. | Unità e pluralità | |
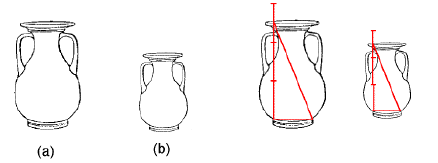
Due forme sono analoghe quando gli elementi che le
costituiscono sono negli stessi rapporti. I vasi (a) e (b), della figura, hanno la stessa forma,
non solo perche’ hanno due manici una base e un collo, ma perche’
i rapporti tra le parti dell’uno sono gli stessi dei rapporti tra le
corrispondenti parti dell’altro. Ad esempio l’altezza e’
circa due volte e mezzo l’attaccatura della base. I vasi (a) e (c) invece non hanno la stesa forma
perché la base del vaso (c) e’ troppo stretta; piu’
precisamente, nel vaso (c), l’altezza e’ circa 5 volte e mezzo
l’attaccatura della base. | Analogia tra forme | |
Il legame che si può creare due grandezze, come
quello che si e’ creato tra la grandezze AB e V considerato
prima, non esiste a priori, non è un dato assoluto, ma dipende solo
dall’esistenza di una terza grandezza, U che sia parte di
entrambe. L’esistenza di una parte così fatta può essere
manifesta in una data situazione, come nel caso che abbiamo considerato,
come può non esserlo. Questo è ciò che accade con i
segmenti CD e CF o tra l’altezza del vaso e la sua imboccatura. Non
esiste immediatamente niente che leghi i due segmenti, e non esisterà
fino a quando la mente non userà un ragionamento e un conseguente
meccanismo di ricerca per appurarlo. Se il ragionamento porta a un risultato
positivo, diremo, in generale, che i due segmenti hanno una ragione comune,
un logos, intendendo con ciò che esiste un terzo segmento che
è parte di entrambi. La parola "ragione" (logos) è il termine
usato dai greci ed è rimasto tale nella lingua inglese (ratio),
mentre in italiano viene usato il termine "rapporto", che esprime anche il
movimento della comparazione: il misurare come un "segnare" secondo un
numero prefissato di volte.
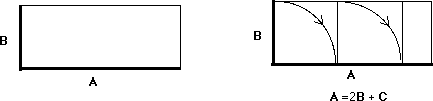
1. Tolgo B da A tante volte fin quando è possibile.
Se il resto è zero, allora B è parte di A,
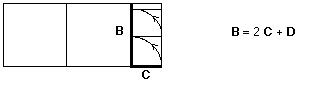
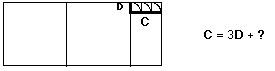
altrimenti avanza qualcosa più piccolo di B 2. Sia C il resto. Tolgo C da B
tante volte fin quando è possibile. Se il resto è zero allora
C è parte di B (e quindi anche di A),
altrimenti 3. Sia D il resto. Tolgo D da C
tante volte fin quando è possibile. Se il resto è zero allora
D è parte di C (e quindi anche di B e di
A), altrimenti 4. E così via......... In questo procedimento il numero interviene ancora solo
per contare le "volte" che un segmento sta in un altro, e a costruire
attraverso esse un rapporto tra le due grandezze iniziali, A e
B. Nell’esempio che abbiamo raffigurato, se D
sta esattamente 3 volte in C come risulta dalla figura, allora,
risalendo, possiamo ritrovare A e B in rapporto a D,
la misura comune: C = 3D, B = 2C + D =
6D+D = 7D, A = 2B + C =
14D+3D=17D e quindi A : B = 17 : 7, il rapporto tra le
grandezze A e B è analogo al rapporto tra i numeri
17 e 7. Il fatto che i resti dopo ogni singolo passo diventassero
sempre piu’ piccoli, fece presagire ai primi pitagorici che questo
metodo dovesse essere universale, che in questo modo ogni rapporto tra
grandezze potesse identificarsi ad un rapporto tra numeri, l’analogia
tra numero e grandezza poneva le basi per un primo universale approccio
scientifico e quantitativo al mondo. Tutte le cose al numero consentono e’ uno dei detti che Pitagora pronunciava
spessissimo davanti a tutti, secondo quanto ci riferisce Giamblico18
. | L'algorimo euclideo delle divisioni successive |
|
La scoperta che esistono grandezze i cui rapporti non
sono esprimibili coi numeri, che esistono rapporti per i quali
l’algoritmo euclideo, pur fornendo ad ogni passo dei resti sempre
piu’ piccoli, va avanti all’infinito, dovette probabilmente
scuotere radicalmente queste convinzioni rimettendo in gioco l’idea
stessa di grandezza, l’idea di infinito, l’idea atomista di un
quanto iniziale col quale esprimere ogni quantità. Nello spazio
geometrico, in un segmento, e’ insita la possibilità di una
divisione all’infinito, la possibilità di trovare infiniti pezzi
sempre più piccoli la cui somma sia finita. L’idea di
continuità contrapposta al discreto riemerge evidenziando
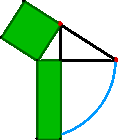
diversità profonde. E’ nel pentagono che, probabilmente, per la
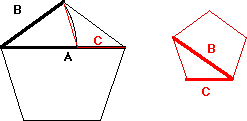
prima volta, questa separazione si e’ chiaramente mostrata. Se A e’ la diagonale del pentagono regolare e
B il suo lato, allora B sta in A una volta e quello che
resta, diciamo C , e’ il lato di un nuovo pentagono, più
piccolo, di cui B e’ la diagonale. B conterrà C una volta con un resto
D che e’ il lato di un nuovo pentagono di diagonale C. Si
capisce che il processo puo’ andare avanti all’infinito
perché e’ sempre A = B +C , B=C+D , C=D+E ,
D=E+F , .... e ogni volta si realizza un nuovo pentagono nel quale,
per quanto piccolo sia, il lato non potrà mai misurare esattamente la
diagonale poiché questa e’ comunque più grande del lato e
più piccola del doppio lato. | Il "non-rapporto" l’irrazionale |
|
Sul versante dei numeri la faccenda è diversa.
Abbiamo visto come i numeri scaturiscano da una unità predefinita,
immutabile, e come ognuno di loro ne sia una pluralità. Questo fatto
porta come conseguenza che di un numero si possa definire la "parte""nello
stesso significato che ha tra le grandezze, ma che sia possibile definire
anche un altro oggetto: le "parti", al plurale: Un numero è parte di un [altro] numero,
il minore di quello maggiore, quando esso misuri il maggiore
[cioè lo divida] "parti" invece di un
numero, quando non lo misuri.19 Ad esempio. Dati il 6, il 5, il 2, diremo che il due
è (la terza) parte di 6, e che è invece due parti di 5. Perché tra le grandezze non è possibile
dare le stesse definizioni iniziali di parte e di parti? Per un motivo
cruciale: riferendoci al prercedente rettangolo, CF, che non è parte
di CD perché non lo misura esattamente, non è detto che ne sia
"parti" che sia cioe’ formato da un certo numero di parti di CD, non
è detto cioè che esista una grandezza U comune a CD e a
CF che le misuri entrambi esattamente dal momento che il ragionamento
esposto non è detto termini in un numero finito di passi. Non
è quindi possibile dire in generale, che se un segmento non ne
misura un altro, ne è comunque un certo numero di parti . | Differenze tra numeri (interi) e grandezze |
|
Il considerare non più le grandezze ma le
pluralità ci ha condotto, fin dai tempi di Pitagora, dalla geometria
all’arimetica, dal continuo al discreto.
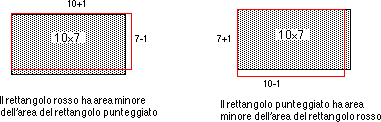
L’immagine geometrica del problema rende manifesto
qualcosa di nuovo che non era richiesto dalla domanda iniziale ma che
contribuisce a aumentare la comprensione del problema. Modificando il
problema senza cambiarne la struttura ci accorgiamo che tanto più
e’ rettangolare la forma del problema tanto più evidente e’
la sua soluzione. Pitagora esponeva i suoi insegnamenti a chi lo frequentava o distesamente o per simboli. Chè il suo insegnamento era di due modi: e quelli che lo frequentavano si distinguevano in matematici e acusmatici. Matematici erano quelli che conoscevano la parte più importante e approfondita della sua dottrina, acusmatici quelli cui erano insegnate soltanto le regole sommarie, senza accurate spiegazioni 20 | Comprensione "per ragionamento" |
|