|
Neuroscienze, apprendimento e didattica della matematica |
 |
| 4. Discorso naturale e discorso
dimostrativo |
||
Credo che oggi ogni insegnante ormai debba accettare il
fatto che non è scontato che tutti gli studenti abbiano un sistema
di lettura adeguato, che permetta loro di leggere fino in fondo e a
comprendere una frase lunga e complessa. Spesso si fermano a metà,
confusi, e, nel caso di un problema, cominciano a risolverlo senza aver
capito cosa questo in realtà richiede e senza sapere quali dati
hanno a disposizione.
Non pochi studenti, nella risoluzione di un problema, sbagliano o si
bloccano già fin dal testo. Normalmente questo viene letto con una
ricerca sequenziale del significato di ogni parola, aspettando che emerga,
vocabolo dopo vocabolo, il significato complessivo del periodo. Questo
però non riesce subito a delinearsi e man mano che ci si inoltra
nella frase il peso e il senso delle parole appena lette svaniscono per
l’aggiungersi, nella memoria di lavoro, di quelle che seguono. | Difficoltà a leggere un testo |
|
Questa difficoltà viene aumentata dal fatto che
spesso questi testi hanno costruzioni sintattiche complicate, nelle quali si
devono accumulare grandi quantità di subordinate prima di incontrare
la principale. E così succede che, pur afferrando qua e là
qualche significato parziale, il senso ultimo del discorso, quello che lega
tutto, si diluisce per via dei legami logici che non si riescono a
stringere, di gerarchie semantiche che non prendono forma. Dobbiamo allora
preoccuparci di insegnare agli studenti che ancora non l’hanno, una
opportuna strategia di pensiero, semplice e per noi addirittura banale, ma
per loro niente affatto spontanea. | Come capire un testo |
|
È da notare, a questo proposito, come sia
frequente incontrare nei testi matematici costruzioni "circolari"
che ostacolano una rapida comprensione della frase: "la superficie
della zona la cui altezza è AC…". Per capire di cosa si sta
parlando, dopo essere arrivati in fondo alla frase dobbiamo fare il percorso
inverso: AC, come altezza, definisce una zona che a sua volta identifica la
superficie che ci interessa. | Costruzioni circolari | |
Questo tipo di costruzione è veramente molto
frequente: i problemi sono spesso formulati "alla rovescia" nel
modo seguente:" Data una circonferenza di centro O e raggio r,
determinare a quale distanza da O si deve condurre una corda MN
affinché sia K il rapporto tra l’area del triangolo formato
dalla corda MN e dalle tangenti al cerchio in M ed N, ed il rettangolo di
lato MN inscritto nel cerchio" piuttosto che in modo diretto, molto
più facile per lo studente:"In una circonferenza di centro O e
raggio r si disegni una corda MN e si chiami x la sua distanza dal centro.
Si costruisca successivamente il rettangolo di lato MN inscritto nel
cerchio. Condotte poi le tangenti al cerchio in M e in N, si consideri il
triangolo formato dalla corda MN e da tali tangenti . Determinare il valore
di x affinché il rapporto tra l’area del triangolo e quella del
rettangolo valga k". | Formulazioni dirette e "alla rovescia" | |
| è dell'anima un logos che accresce se stesso Eraclito |
Si potrebbe a questo punto osservare che forse sarebbe
più economico e razionale se ci impegnassimo tutti quanti a mettere i
ragazzi di fronte a frasi ordinate in modo diretto invece di costringerli a
imparare il latino per capire quelle formulate alla rovescia. In
realtà credo che evitare del tutto "palestre" mentali di
questo tipo sia dannoso. Si possono cambiare materie, contenuti, metodi, ma
deve rimanere qualcosa che abbia sulle menti la capacità di
potenziare con esercizi artificiali questi processi naturali. Penso che il
senso e l’utilità dell’operazione di sintesi effettuabile
dal pensiero tramite i concetti verbali e le immagini mentali siano inoltre
estremamente più estesi di quanto può essere apparso dagli
esempi riportati. Credo in effetti che questa operazione sia alla base di
tutto il pensiero e ne accompagni ogni manifestazione, da quelle più
semplici a quelle più complesse. Sto parlando in breve di una
capacità dei processi del pensiero a "pensare" strutturando
blocchi d’informazione, partendo dal materiale percettivo immediato per
estendere poi il processo in una sorta di ricorsività, costruendo
moduli sempre più ampi, in cui gli elementi costituenti sono i
blocchi più piccoli. La ricorsività è basata proprio
sul fatto che "una stessa operazione" avviene a vari
livelli. | |
Questi limiti della memoria di lavoro regolano anche il
nostro pensiero "discorsivo", il modo cioè con cui parliamo
e argomentiamo con intenti persuasivi nella vita comune, a anche in questo
caso si notano differenze non trascurabili con il pensiero scientifico.
Mosconi 9ci presenta un esempio di incongruenza tra discorso
persuasivo (naturale) e discorso dimostrativo (scientifico) usando un
teorema degli Elementi, quello conosciuto come primo teorema di
Euclide. Questo teorema è di estrema importanza perché da esso
è facile dedurre il teorema di Pitagora alla base della geometria
analitica metrica. E’ infatti il teorema di Pitagora che consente di
collegare la distanza tra due punti del piano cartesiano ad una formula
algebrica che coinvolge i valori delle coordinate dei due punti. Col teorema
di Pitagora si introduce nello spazio una metrica che conferisce a quello
spazio la struttura, come oggi si dice, di spazio euclideo. Mosconi osserva
come un criterio seguito dai matematici nell’esporre dimostrazioni
geometriche è quello di non fare mai alcuna affermazione che non sia
suffragata da elementi forniti in precedenza. Detto per inciso, è
anche uno dei comportamenti che insegniamo e pretendiamo dai nostri alunni.
In sostanza, nel corso della dimostrazione, nulla viene anticipato e il
destinatario del discorso si trova spesso nella situazione di venir condotto
verso la conclusione finale un po’ come un cieco che, pur conoscendo la
meta, può controllare la strada solo passo dopo passo, senza rendersi
conto della totalità dell’itinerario. Mosconi mostra come
"si può organizzare il discorso dimostrativo secondo un criterio
diverso […]preoccupandosi di organizzare il discorso con riguardo alla
maniera di funzionare della sua mente, a ciò che può favorirne
la comprensione e facilitarne il ricordo" |
Discorso naturale e discorso dimostrativo |
|
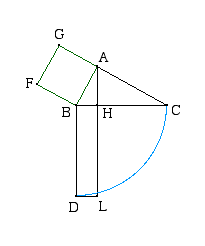
Il teorema di Euclide dice che: | Teorema di Euclide | |
Negli Elementi troviamo la dimostrazione esposta
nel modo seguente:
| La dimostrazione di Euclide | |
Mosconi osserva come ad ogni passo, almeno fino
al punto 6, l’ascoltatore non è in grado di comprendere in
ordine all’obiettivo finale la funzione delle operazioni che vengono
compiute, vale a dire che per gran parte della dimostrazione il ricevente
procede alla cieca. La strategia espositiva del testo euclideo costringe il
soggetto a ricevere e conservare per un certo tempo una notevole massa di
informazioni come elemento o dati irrelati, non inseribili o connettibili in
un piano chiaramente compreso o intravisto. Le informazioni devono essere
accolte una per una in piccoli blocchi o microstrutture, in attesa che si
delinei il piano della dimostrazione e si determini l’organizzazione
concettuale del discorso. Una tale strategia espositiva comporta
notevolissimi rischi di caduta o di deterioramento dell’informazione
trasmessa. | Riordinamento della dimostrazione | |
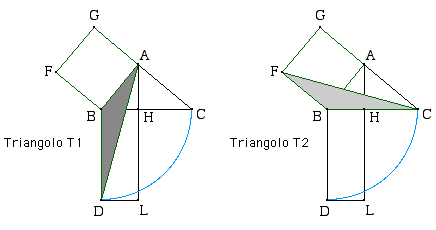
Ecco ora il nuovo sviluppo della dimostrazione:
Questo è il punto essenziale della dimostrazione che può essere ben illustrato con una animazione.
Il punto P si muove sul segmento AL descrivendo tutti triangoli equivalenti perché hanno la stessa base BD fissa e la stessa altezza DL. Quando P si trova in L abbiamo il mezzo rettangolo, quando invece si trova in A abbiamo il triangolo T1. E’ a questo punto che si usa l’ipotesi essenziale che il triangolo sia rettangolo in A perché questo garantisce l’allineamento dei punti G,A,C [corrisponde al punto 3 del testo precedente]. Questa animazione permette di rendersi conto di cosa succeda se il triangolo non è rettangolo.
Tutto quello che è stato fatto finora continua a valere. Ciò che invece non vale più se G,A,C non sono llineati è il fatto che l’area del triangolo FBC è la metà dell’area del quadrato. "come dovevasi dimostrare" | L'uso delle animazioni geometriche | |
In questa dimostrazione i passi che vengono
effettuati fanno quasi sempre riferimento al focus del problema, rendendo
più agevole seguire il discorso: al punto 3 vengono determinati i
rapporti tra una figura focus, il rettangolo, e un’altra figura,
ausiliaria, aggiunta dal geometra (l’idea della dimostrazione) il
triangolo ABD, al punto successivo si determinano i rapporti tra
l’altra figura focus, il quadrato, e il secondo triangolo, la cui
chiamata in causa ha un evidente parallelismo con il caso precedente,
qualora valga l’ipotesi che il triangolo dato sia rettangolo in A. | Il focus | |