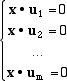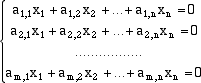|
Spazio ortogonale a un dato sottospazio. Dimensione dello spazio ortogonale.
Consideriamo in tutto questo paragrafo uno spazio vettoriale V di dimensione finita con un prodotto scalare. Spazi di questo tipo sono tutti i sottospazi di
Rn o di uno spazio di vettori geometrici.
Sia U un sottospazio vettoriale di V. Si definisce lo spazio ortogonale di U il sottospazio
U^ i cui vettori sono tutti i vettori di V ortogonali ad ogni vettore di U. In simboli
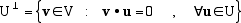
Lo spazio ortogonale è molto importante in vari contesti soprattutto perché si lega allo spazio delle soluzioni
di un sistema di equazioni lineari omogeneo. Se infatti u1, u2, ... , um sono
vettori numerici a n componenti e se
U = Span(u1, u2, ... , um)
allora lo
spazio ortogonale ad U è dato da tutti i vettorio x = (x1,x2, ... , xn) tali che
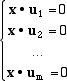
Se U è un sottospazio di Rn cioè se i dati vettori u1,
u2, ... , um sono vettori numerici a n componenti, allora esplicitando il prodotto,
il sistema precedente diventa
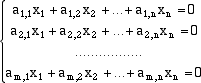
dove i coefficienti ai,j sono le componenti dei dati vettori ui.
La considerazione delle basi ortonormali e l'algoritmo di Gram-Schmidt permettono di dimostrare un importante teorema che lega la
dimensione di U^ con quella di U.
Teorema
Sia V uno spazio vettoriale di dimensione finita dotato di un prodotto scalare e U un suo sottospazio. Risulta allora
dim U + dim U^ = dim V
Dimostrazione
A partire da un insieme di generatori di U costruiamo una sua base ortonormale (ad esempio con l'algoritmo di Gram-Schmidt). Sia
k= dim U e
{e1, e2, ... , ek} base ortonormale di U
completiamo questa base fino a trovare una base di V, cosa, come abbiamo visto,
sempre possibile e ortonormalizziamo questa base (ad esempio con l'algoritmo di Gram-Schmidt): sia dunque h+k = dim V e
{e1, e2, ... , ek, f1, f2, ... ,
fh}
base ortonormale di V
Osserviamo ora che i vettori f1, f2, ... ,fh sono vettori di
U^ linearmente indipendenti essendo ortogonali a ogni vettore della base di U. Quindi
U^ É Spam(f1,
f2, ... ,fh)
D'altra parte i vettori f1, f2, ... ,fh generano
U^. Se invatti v è un vettore di U^, allora, essendo anche un vettore di V, posso scriverlo come combinazione lineare dei vettori della base di V, cioé
v = a1e1 + a2e2 + ... + akek +
b1f1 + b2f2 +... + bhfh
ma v è un vettore di U ^ dunque
v.e1 = v.e2 = ... =
v.ek = 0
e quindi a1 = a1 = ... = ak = 0 e v risulta combinazione lineare dei vettori f
che quindi generano U^.
Questo teorema permette di "contare" le soluzioni di un sistema omogeneo di m equazioni lineari in n incognite: se le equazioni sono
indipendenti cioé se i vettori numerici a n componenti u1, u2, ... , um, sono
linearmente indipendenti allora esistono n-m soluzioni linearmente indipendenti dato che, in questo caso dim U = m e dim V = n. In generale per risolvere il
dato sistema e sapere quante sono le sue soluzioni indipendenti, si dovrà determinare la dimensione di U e ciò, come vedremo,
potrà essere fatto con un semplice algoritmo che permette di estrarre da un sistema qualunque di vettori numerici il suo sottosistema
massimale di vettori indipendenti.
Osserviamo anche che le infinite soluzioni del sistema omogeneo, che, come abbiamo detto, si riproducono combinamdosi linearmente tra loro
e generando
uno spazio vettoriale, possono essere descritte a partire da un numero finito di loro. Il numero minimo di soluzioni attraverso le quale ottenere
tutte le altre è proprio la dimensione dello spazio delle soluzioni. Anche per questo, come vedremo, esiste un algoritmo capace di calcolare esplicitamente
una base per lo spazio delle soluzioni. In questo modo, attraverso un calcolatore, che può gestire solo oggetti finiti, possiamo ugualmente descrivere
le infinite soluzioni calcolando una base, che è sempre finita , dello spazio vettoriale U^.
| |