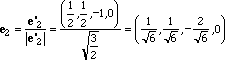e questo numero è nullo se e solo se u = 0, altrimenti è un numero reale positivo. Un insieme di vettori {e₁,e₂,...,e_k} formano un a famiglia di vettori ortonormale se sono a due ortogonali e di modulo 1. In formule:

dove d_i,j è il simbolo di Kroneker che vale 1 se i = j, zero altrimenti.
Una base di V formata da un insieme di vettori ortonormale, si chiama una base ortonormale di V. La base {i, j, k} dello spazio dei vettori geometrici è una base ortonormale. Anche la base canonica di Rⁿ formata dai vettori (1,0,0,...,0), (0,1,0,...,0), (0,0,1,..,0), ... , (0,0,0,...,1) è una base ortonormale. Queste basi sono molto utili, come abbiamo visto, nello studio di questi spazi. Ad esempio se {e₁,e₂,...,e_n} è una base ortonormale di V allora le componenti di un qualunque vettore u, in quella base, sono le sue proiezioni ortogonali sui vettori e_i. In altri termini il vettore ammette sempre una decomposizione ortonormale, cioè risulta sempre:

si vede facilmente che V ha dimensione minore di 4 essendo un sottospazio di R⁴, inoltre i 3 vettori di V

sono linearmente indipendenti e dunque V è di dimensione 3. Tuttavia questi vettori non sono ortogonali tra loro. Ad esempio u₁ non è ortogonale a u₂ dato che u₁.u₂ = -1. Anche dal punto di vista dei moduli questi vettori non vanno bene dato che hanno tutti come modulo la radice di 2.

L'algoritmo di Gram-Schmidt, che ora esponiamo, da un procedimento per ricavare da un qualunque insieme di generatori di un dato spazio vettoriale, una base ortonormale. Sia

• Se u₁ = 0 eliminiamolo dal nostro elenco. Sarà ancora Span(u₁, u₂, ... , u_m) = Span(u₂, ... , u_m). Se invece u₁ non è zero sostituiamolo con il suo normalizzato cioè col vettore

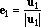
  Il vettore e₁ ha modulo 1 e Span(u₁, u₂, ... , u_m) = Span(e₁, u₂, ... , u_m) dato che
  e₁ Î Span(u₁, u₂, ... , u_m) e u₁ Î Span(e₁, u₂, ... , u_m).
  Se i vettori della lista sono esauriti, l'algoritmo è finito: {e₁} è una base ortonormale di V e dim V = 1, altrimenti tra i generatori di V esiste un altro vettore u₂

• Togliamo da u₂ la sua proiezione ortogonale di su e₁ in modo che il vettore restante e'₂ = u₂ - (u₂.e₁)e₁

  sia ortogonale a e₁. Se e'₂ = 0 allora u₂, essendo combinazione lineare di e₁, può essere tolto dalla lista e Span(e₁, u₂, ... , u_m) = Span(e₁, ... , u_m). Altrimenti sostituiamo u₂ con il normalizzato di e'₂ cioè con
  

  

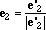
  A questo punto e₁ e e₂ sono due vettori di modulo 1 e ortogonali tra loro. Inoltre

  V= Span(e₁, u₂, ... , u_m)=Span(e₁, e₂, ... , u_m)

  dato che e₂ Î Span(e₁, u₂, ... , u_m) e u₂ Î Span(e₁, e₂, ... , u_m).
  Se i vettori della lista sono esauriti, l'algoritmo è finito:{e₁,e₂} è una base ortonormale di V e dimV = 2, altrimenti tra i generatori di V esiste un altro vettore u₃ e possiamo iterare il procedimento.

• Togliamo da u₃ la sua proiezione ortogonale sullo spazio generato da e₁ e e₂ in modo che il vettore restante e'₃ = u₃ - [(u₃.e₁)e₁ + (u₃.e₂)e₂]

  sia ortogonale sia a e₁ che a e₂. Se e'₃ = 0 allora u₃, essendo combinazione lineare di e₁ ed e₂ , può essere tolto dalla lista e Span(e₁, e₂, u₃ ... , u_m) = Span(e₁, e₂, ... , u_m). Altrimenti sostituiamo u₃ con il normalizzato di e'₃ cioè con
  

  

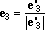
  A questo punto e₁ , e₂ , e₃ sono tre vettori di modulo 1 e ortogonali tra loro a due a due. Inoltre

  V= Span(e₁, e₂, u₃, ... , u_m)= Span(e₁, e₂, e₃, ... , u_m)

  dato che e₃ Î Span(e₁, e₂, u₃, ... , u_m) e u₃ Î Span(e₁, e₂, e₃, ... , u_m)
  Se i vettori della lista sono esauriti, l'algoritmo è finito: {e₁,e₂,e₃} è una base ortonormale di V e dim V = 3, altrimenti iteriamo il procedimento col vettore successivo fino ad esaurimento dei vettori.

dove

e applichiamo l'algoritmo di Gram-Schmidt a questi tre vettori.

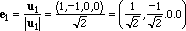
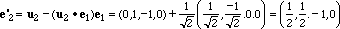
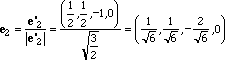
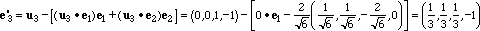
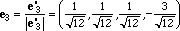
Si vede immediatamente che i tre vettori {e₁,e₂,e₃} sono vettori di V dal momento che la somma delle loro componenti è zero e inoltre sono di modulo 1 e a due a due ortogonali.