Unità 3

Matematica discreta 2

Complementi ed esercizi dell'Unità 3.

Basi e dimensione di uno spazio vettoriale

Come abbiamo visto esistono diverse situazioni nelle quali gli elemti di un derminato insieme V possono sommarsi e moltiplicarsi per uno scalare riproducendosi reciprocamente. In questo caso, e se le operazioni rispettano certe regole di base, l'insieme V è uno spazio vettoriale. Accade spesso che lo spazio V sia formato dalla totalità delle soluzioni di un determinato problema soluzioni che vorremmo poter trovare e descrivere compiutamente. La difficoltà consiste spesso nel fatto che tali soluzioni sono infinite ed è quindi impossibile elencarle una dopo l'altra. Uno dei vantaggi dell'algebra degli spazi vettoriali sta proprio nel fatto che essa permette di descrivere infiniti elementi a partire da un numero finito di loro, nello stesso modo in cui possiamo descrivere gli infiniti punti di una retta a partire da due soli suoi punti distinti A e B, o gli infiniti colori a partire dai tre colori base e dal loro relativo dosaggio. Una cosa analoga avviene negli spazi vettoriali oggetto del nostro studio: ogni vettore può essere espresso come combinazione lineare di un dato numero fisso di vettori: variando i coefficienti della combinazione si descrivono tutti i possibili infiniti vettori dello spazio che si sta considerando. Il modo migliore e più semplice per fare questo è quello di prendere il minor numero possibile di generatori che in questo caso vengono a formare ciò che si chiama una base dello spazio vettoriale.

Definizione
Diciamo che un sistema di vettori B = {u₁, u₂, ... , u_n} è una base di V se
(i) u₁, u₂, ... , u_n generano tutto lo spazio
(ii) u₁, u₂, ... , u_n sono linearmente indipendenti

La prima condizione significa che ogni vettore v dello spazio si può scrivere come come combinazione lineare dei vettori della base, mentre la seconda rende in un certo senso minimo il numero di generatori perché se uno degli u fosse combinazione lineare degli altri, quelli basterebbero a generare tutto lo spazio.

Un fatto importante basato su una semplice proprietà dei sistemi omogenei di equazioni lineari è espresso dal lemma seguente.

Lemma
Se k+1vettori di uno spazio vettoriale V sono ognuno combinazione lineare di k vettori fissi, allora i k+1 vettori sono linearmente dipendenti.

Dimostrazione
Siano v₁, v₂, ... , v_k+1 i k+1 vettori che sono ognuno combinazione lineare degli stessi vettori u₁, u₂, ... , u_k. Abbiamo allora

v₁ = a_1,1u₁ + a_1,2u₂ + ... + a_1,ku_k
v₂ = a_2,1u₁ + a_2,2u₂ + ... + a_2,ku_k
................................................
v_k+1 = a_k+1,1u₁ + a_k+1,2u₂ + ... + a_k+1,ku_k

Per dimostrare che i vettori v sono linearmente dipendenti dobbiamo poter trovare una loro combinazione lineare nulla non banale, dobbiamo cioè poter trovare k+1 scalari non tutti nulli tali che

x₁v₁ + x₂v₂ + ... + x_k+1v_k+1 = 0

Sostituiamo in questa relazione i vettori v con le loro combinazioni lineari. Troviamo

0 = x₁(a_1,1u₁ + a_1,2u₂ + ... + a_1,ku_k) +
   + x₂(a_2,1u₁ + a_2,2u₂ + ... + a_2,ku_k) +
      ..................................
+x_k+1(a_k+1,1u₁ + a_k+1,2u₂ + ... + a_k+1,ku_k)

espressione questa che, distibuendo la somma e raccogliendo i coefficenti dei vari vettori u, cosa possibile in ogni spazio vettoriale,diventa

      (x₁a_1,1 + x₂a_2,1 + ... + x_k+1a_k+1,1)u₁ +
    + (x₁a_1,2 + x₂a_2,2 + ... + x_k+1a_k+1,2)u₂ +
      ..................................
    + (x₁a_1,k + x₂a_2,k + ... + x_k+1a_k+1,k)u_k

Quest'ultima relazione è sicuramente soddisfatta se troviamo degli scalari x₁, x₂, ... , x_k+1 non tutti nulli tali che

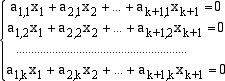Il sistema che abbiamo scritto è un sistema omogeneo di k equazioni lineari in k+1 incognite. Questo sistema ammette sempre una soluzione non nulla. Possiamo infatti, dalla prima equazione ricavare una incognita e sostituirla nelle altre equazioni riducendo così il sistema a un sistema in k incognite e k-1 equazioni. Da una soluzione non nulla di questo nuovo sistema, possiamo risalire a una soluzione non nulla per il sistema iniziale. Abbiamo in questo modo ridotto il problema a un sistema più piccolo. Proseguendo in questo modo alla fine arriviamo a un sistema in una sola equazione e due incognite. È ovvio che quest'ultimo sistema ammette sempre una soluzione non nulla.

Questo lemma ci permette di dimostrare il risultato principale relativo alle basi di uno spazio vettoriale.

Teorema
Suppoiniamo che B = {u₁, u₂, ... , u_n} sia una base per uno spazio vettorialeV, allora
(i) comunque si scelgano n+1 vettori in V, questi sono linearmente dipendenti
(ii) comunque si scelgano n-1 vettori in V, questi non generano tutto lo spazio.

Dimostrzione
Poiché B è una base di V i suoi vettori generano tutto lo spazio e quindi gli n+1 vettori dati si scrivono come combinazioni lineari degli n vettori di B. Ma il lemma ci dice che allora essi sono linearmente dipendenti. Se poi fosse possibile generare lo spazio con n-1 vettori allora sarebbe possibile scrivere gli n vettori della base B come combinazioni lineari di quelli e quindi, per il lemma, dovrebbero essere linearmente dipendenti, mentre, facendo parte di una base essi sono indipendenti.

Ovviamente il teorema implica anche, a forziori, che se la spazio vettoriale V ha una base formata da n vettori allora un qualunque insieme di m vettori di V non può essere formato da vettori linearmente indipendenti se m > n, e non può generare tutto lo spazio se m < n. Da questo teorema seguono vari corollari.

Corollario 1
Due basi diverse di uno stesso spazio vettoriale hanno lo stesso numero di elementi.

Infatti, se la prima base ha n elementi, la seconda base non può averne di più perché questi sarebbero indipendenti e nello spazio non ci sono più di n vettori indipendenti. D'altra parte non possono neppure essere meno di n perché in quel caso avremmo meno di n vettori che generano la spazio.

Il numero di vettori di una qualunque base di una spazio vettoriale V si chiama la dimensione dello spazio e si indica con dim V.

Un procedimento spesso efficace per trovare una base di un dato spazio vettoriale consiste in questo:

Si cerca un vettore non nullo u₁ dello spazio V. Se tale vettore non esiste vuol dire che V ha solo il vettore nullo e non c'è nulla da dire, se invece tale vettore esiste {u₁} è un vettore linearmente indipendente e si va al punto successivo
se {u₁} genera tutto lo spazio allora è una base e dim V= 1. Altrimenti esiste un vettore u₂ che non è multiplo di u₁, i vettori u₁ e u₂ sono linearmente indipendenti e si va al punto successivo
se {u₁, u₂} generano tutto lo spazio allora sono una base e dim V= 2. Altrimenti esiste un vettore u₃ che non è combinazione lineare di u₁ e u₂, i vettori u₁, u₂, u₃ sono linearmente indipendenti e si va al punto successivo.
se {u₁, u₂, u₃} generano tutto lo spazio allora sono una base e dim V= 3. Altrimenti esiste un vettore u₄ che non è combinazione lineare di u₁ e u₂, u₃ e i vettori u₁, u₂, u₃ , u₄ sono linearmente indipendenti e si prosegue ricorsivamente.

Se si volesse implementare questa startegia in un programma al calcolatore, sarebbe necessario indicare un algoritmo per calcolare esplicitamente, a ogni passo, l'eventuale vettore che non è combinazione degli altri cosa non facile. Nella pratica, volendo usare questo procedimento, ci si orienta a occhio seguendo una qualche intuizione ma in molti casi quasta non basta e non si sa come procedere come ad esempio nel caso che abbiamo visto dei quadrati magici. Sviluppando la teoria, riusciremo, per altra via, a dare un esplicito ed effettivo algoritmo per risolvere completamente il problema. In ogni caso, se il procedimento che abbiamo descritto ha termine dopo un numero finito di passi (cosa che non sempre avviene) la spazio vettoriale V ha dimensione finita altrimenti V ha dimensione infinita. La teoria degli spazi vettoriali di dimensione infinita, pur essendo di estremo interesse, esula dagli scopi di questo corso. Gli spazi vettoriali che prenderemo in esame saranno tutti, salvo esplicita menzione, di dimensione finita.

Da queste definizioni e dalla costruzione precedente deriva anche il seguente

Corollario 2
Se V è uno spazio vettoriale di dimensione n allora
(i) n vettori linearmente indipendenti generano V
(ii) n vettori che generano V sono linearmente indipendenti

Dimostriamo (i) Se, per assurdo, gli n vettori linearmente indipendenti non generassero tutto lo spazio esisterebbe un n+1-esimo vettore che non risulta esprimibile come loro combinazione lineare e che sarebbe, dunche, linearmente indipendente da quelli. In questo modo si troverebbero n+1 vettori linearmente indipendenti cosa che contraddice la parte (i) del teorema dato che lo spazio ha una base formata da n vettori. Per (ii) si procede in modo analogo.