Overview of the Proof
Purely for the sake of illustration, i.e.
so we can concentrate on the methodology rather
than digress about what are the correct, [M3],
statements about the hyperbolicity of algebraic
surfaces, let's suppose that the goal is to
prove the Green-Griffiths conjecture, viz:
there are no Zariski dense entire curves on
surfaces of general type. This was proved for
surfaces with big co-tangent bundle in [M1].
Post factum, op. cit.
is the key point in the classification, [M2],
of foliations,
![$ S\rightarrow [S/\mathcal{F}]$](img1.png) on algebraic
surfaces, where, strictly speaking, around
the singularities the champ classifiant
on algebraic
surfaces, where, strictly speaking, around
the singularities the champ classifiant
![$ [S/\mathcal{F}]$](img2.png) is purely notational,
and, otherwise as per [SGA.I] exposé VI.
The general case of the conjecture
was reduced by Green & Griffiths, [GG], to
entire curves satisfying a
is purely notational,
and, otherwise as per [SGA.I] exposé VI.
The general case of the conjecture
was reduced by Green & Griffiths, [GG], to
entire curves satisfying a 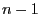 dimensional
order O.D.E.,
dimensional
order O.D.E.,
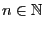 , on an algebraic
surface, so, in particular a Zariski dense
entire curve invariant by a foliation by
curves on a variety of dimension
, on an algebraic
surface, so, in particular a Zariski dense
entire curve invariant by a foliation by
curves on a variety of dimension 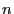 .
As such the basic strategy is to make
this key point in the classification
theory of foliations work in all dimensions.
It now fits into a general structure, and
may be succinctly summarised,
.
As such the basic strategy is to make
this key point in the classification
theory of foliations work in all dimensions.
It now fits into a general structure, and
may be succinctly summarised,
 (a)
(a)
- One first resolves the singularities.
This means, functorially with respect to the
ideas, that the relative dualising sheaf,
![$ \omega_{S/[S/\mathcal{F}]}$](img6.png) , abbreviated to
, abbreviated to
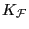 ,
has canonical singularities. This step is
absolutely essential, otherwise
,
has canonical singularities. This step is
absolutely essential, otherwise
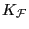 has absolutely no relation with the curvature
of the leaves, and one might as well study
giraffes or cockatoos, e.g. consider
the foliation
has absolutely no relation with the curvature
of the leaves, and one might as well study
giraffes or cockatoos, e.g. consider
the foliation
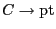 for
for
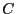 Gorenstein with singularities cusps, then
we can easily ensure that the trichotomy of
the uniformisation theorem for smooth curves
(which for reasons of dimension is the same
as having canonical singularities) is devoid
of meaning if we only suppose Gorenstein.
Gorenstein with singularities cusps, then
we can easily ensure that the trichotomy of
the uniformisation theorem for smooth curves
(which for reasons of dimension is the same
as having canonical singularities) is devoid
of meaning if we only suppose Gorenstein.
 (b)
(b)
- The next step is to make a minimal
model, i.e. either
![$ S\rightarrow [S/\mathcal{F}]$](img1.png) is a conic bundle or
is a conic bundle or
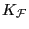 nef. This
can be done by blowing down chains of invariant
rational curves. As a result to maintain an
ambient smooth space,
nef. This
can be done by blowing down chains of invariant
rational curves. As a result to maintain an
ambient smooth space, 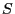 , one needs to pass to
the 2-category of champs de Deligne Mumford,
albeit extremely simple ones. There is a
related notion of canonical model, [M2],
which leads to more precise results, but in
the first instance we don't need it.
, one needs to pass to
the 2-category of champs de Deligne Mumford,
albeit extremely simple ones. There is a
related notion of canonical model, [M2],
which leads to more precise results, but in
the first instance we don't need it.
 (c)
(c)
- Now we need to measure the curvature
of
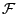 invariant discs
invariant discs
 .
Basically the statement is,
where
.
Basically the statement is,
where
 is the Poincaré metric on
the disc. However, the inequality should be
understood as one of metricised line bundles
on pointed (i.e. the Green's function
is well defined, and one can take the degree
in the sense of Nevanlinna theory) discs, so
there are (necessary) subtleties about the
proximity of the origin to the singularities
and/or invariant curves through the same which
are being glossed over, cf. [M4] III.2.2.
is the Poincaré metric on
the disc. However, the inequality should be
understood as one of metricised line bundles
on pointed (i.e. the Green's function
is well defined, and one can take the degree
in the sense of Nevanlinna theory) discs, so
there are (necessary) subtleties about the
proximity of the origin to the singularities
and/or invariant curves through the same which
are being glossed over, cf. [M4] III.2.2.
 (d)
(d)
- Let's say the goal is to prove that
there is no Zariski dense invariant entire curve, albeit
compactness of invariant discs with bubbles
is the real theorem, and only marginally
more difficult. Either way, should the goal
be false, then by (c) we find
an invariant measure
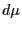 which must satisfy,
Without loss of generality
which must satisfy,
Without loss of generality 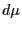 has non-negative
intersection with every effective Cartier divisor,
so by (b),
The Hodge index theorem then applies to
conclude that
has non-negative
intersection with every effective Cartier divisor,
so by (b),
The Hodge index theorem then applies to
conclude that
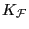 and
and 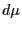 are parallel in
are parallel in
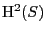 . Philosophically,
this is the key difference between the Mori
theory of foliations and that of varieties.
In the latter case, when the situation
is neither fano nor
general type one invariably seeks a special
representative of the canonical class in the
form of an effective divisor. For foliations
this is a known impossibility, e.g.
poly-disc quotients, but, even if auto-duality
in the middle dimension is obscuring the
point on surfaces, one can find an invariant
measure which is in duality with
. Philosophically,
this is the key difference between the Mori
theory of foliations and that of varieties.
In the latter case, when the situation
is neither fano nor
general type one invariably seeks a special
representative of the canonical class in the
form of an effective divisor. For foliations
this is a known impossibility, e.g.
poly-disc quotients, but, even if auto-duality
in the middle dimension is obscuring the
point on surfaces, one can find an invariant
measure which is in duality with
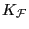 .
.
 (e)
(e)
- Now invariant measures do not grow
on trees. They have very particular properties,
amongst which is that their intersection with
invariant bundles is governed by a residue
at the singularities. Away from the singularities,
transversals yield an étale covering of
the champs classifiant, so
![$ K_{[S/\mathcal{F}]}$](img19.png) is such a bundle, and, of course,
An appropriate version of the residue lemma,
albeit much stronger versions are available
on surfaces, is:
where
is such a bundle, and, of course,
An appropriate version of the residue lemma,
albeit much stronger versions are available
on surfaces, is:
where
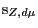 is the Lelong
number around the singular locus
is the Lelong
number around the singular locus 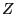 , while
the notation
, while
the notation
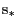 is to provide
for its higher dimensional generalisation
the Segre class, which is functorially,
the ``usual'' Cauchy winding number around
the singularities.
is to provide
for its higher dimensional generalisation
the Segre class, which is functorially,
the ``usual'' Cauchy winding number around
the singularities.
 (f)
(f)
- Finally we put everything together. To
begin with suppose at least one of
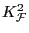 ,
,
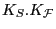 is non-zero. In the former case there cannot
be an invariant entire curve by the curvature
estimate (c). In the latter case without the
former
is non-zero. In the former case there cannot
be an invariant entire curve by the curvature
estimate (c). In the latter case without the
former
![$ K_{\mathcal{F}}.K_{[S/\mathcal{F}]}\neq 0$](img27.png) ,
so by (e)
,
so by (e)
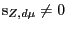 . On a
surface it follows from [S] that if
the class of
. On a
surface it follows from [S] that if
the class of 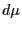 is not big, then it is
effective. If, however, it were big then
is not big, then it is
effective. If, however, it were big then
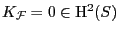 and up
to an étale cover the foliation is given
by a global vector field. If it were effective,
then on the canonical model it is parallel
to an invariant rational or elliptic curve,
and up
to an étale cover the foliation is given
by a global vector field. If it were effective,
then on the canonical model it is parallel
to an invariant rational or elliptic curve,
 with
with  , and the foliation is what
is termed Ricatti or turbulent, i.e.
transverse to a conic, respectively elliptic,
bundle. Whence,
and Riemann-Roch shows that the only other
foliations that can admit entire invariant
curves not factoring through a fixed
sub-variety are elliptic fibrations. Irrespectively,
for
, and the foliation is what
is termed Ricatti or turbulent, i.e.
transverse to a conic, respectively elliptic,
bundle. Whence,
and Riemann-Roch shows that the only other
foliations that can admit entire invariant
curves not factoring through a fixed
sub-variety are elliptic fibrations. Irrespectively,
for 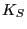 big, the original context of
[M1], it's pretty trivial that
big, the original context of
[M1], it's pretty trivial that
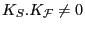 and that there
is no rational or elliptic curve with
and that there
is no rational or elliptic curve with 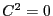 .
.
This discussion is close to optimal, even
from the more limited perspective of the hyperbolicity
of algebraic surfaces as is evidenced by
nos. 10-13 of the F.A.Q..
It applies whenever the co-tangent bundle
of the surface is big, e.g.
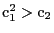 .
As has been said,
Green & Griffiths themselves, [GG],
established the reduction of their
conjecture for surfaces to the study
of foliations by curves on higher
dimensional varieties. The
dimension in question being limited
as a function of the ratio of
.
As has been said,
Green & Griffiths themselves, [GG],
established the reduction of their
conjecture for surfaces to the study
of foliations by curves on higher
dimensional varieties. The
dimension in question being limited
as a function of the ratio of
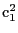 to
to
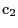 . Close to
the Castelnuovo line, the dimension
is potentially so large as to have
the same practical effect as being
arbitrary. As such, we need to understand
the above schema
for a foliation
. Close to
the Castelnuovo line, the dimension
is potentially so large as to have
the same practical effect as being
arbitrary. As such, we need to understand
the above schema
for a foliation
![$ X\rightarrow [X/{\mathcal{F}}]$](img37.png) by curves
in arbitrary dimension, viz:
by curves
in arbitrary dimension, viz:
 (
( )
)
- Lemma 1: Resolution of Singularities. This
means exactly as for surfaces, i.e.
relative canonicity of the arrow
![$ X\rightarrow [X/{\mathcal{F}}]$](img37.png) . In
practice this means as follows: whenever
the foliation is Gorenstein it is defined
by a vector field
. In
practice this means as follows: whenever
the foliation is Gorenstein it is defined
by a vector field 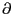 . Should
. Should
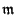 be the maximal ideal
of a singularity in its local ring,
then the Leibniz rule implies that,
is
be the maximal ideal
of a singularity in its local ring,
then the Leibniz rule implies that,
is
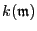 linear, and
it may be shown [M5] I.6.12, that
this endomorphism is linear iff the
singularity is log-canonical. For foliations
by curves, the difference between canonical
and log-canonical is slight, [MP1] III.ii,
and it's easy to go from a log-canonical
resolution to a canonical one. More
importantly to maintain a smooth ambient, resolution
can only be achieved, op. cit. III.iii, in
the 2-category of champs de Deligne-Mumford.
A similar phenomenon was already encountered
in the minimal model theory of surfaces,
and poses no real difficulty to the programme,
albeit by
linear, and
it may be shown [M5] I.6.12, that
this endomorphism is linear iff the
singularity is log-canonical. For foliations
by curves, the difference between canonical
and log-canonical is slight, [MP1] III.ii,
and it's easy to go from a log-canonical
resolution to a canonical one. More
importantly to maintain a smooth ambient, resolution
can only be achieved, op. cit. III.iii, in
the 2-category of champs de Deligne-Mumford.
A similar phenomenon was already encountered
in the minimal model theory of surfaces,
and poses no real difficulty to the programme,
albeit by 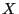 one should understand from
now on a smooth champ with projective
moduli rather than a variety. In any
case op. cit. proves resolution in
dimension 3, and arbitrary dimension
is progressing well.
one should understand from
now on a smooth champ with projective
moduli rather than a variety. In any
case op. cit. proves resolution in
dimension 3, and arbitrary dimension
is progressing well.
 (
(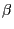 )
)
- Lemma 2: Minimal Models. Just as
for surfaces, albeit after contractions and flips,
there is a dichotomy, either,
![$ X\rightarrow [X/{\mathcal{F}}]$](img37.png) is a conic
bundle, or
is a conic
bundle, or
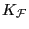 is nef. Supposing
that one starts from some,
is nef. Supposing
that one starts from some,
![$ X\rightarrow [X/{\mathcal{F}}]$](img37.png) with canonical singularities this is done in
all dimensions, [M5], and the final result
of the algorithm is again a smooth champs de
Deligne-Mumford. This may surprise experts
in usual Mori theory, but, nowadays this
should really be called Kawamata theory,
whereas the original emphasis of Mori on
rational curves is what works well for
foliations by curves.
with canonical singularities this is done in
all dimensions, [M5], and the final result
of the algorithm is again a smooth champs de
Deligne-Mumford. This may surprise experts
in usual Mori theory, but, nowadays this
should really be called Kawamata theory,
whereas the original emphasis of Mori on
rational curves is what works well for
foliations by curves.
 (
(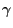 )
)
- Lemma 3: Tautological Inequality. As
per (c) for surfaces, this is something that can
only make sense if
![$ X\rightarrow [X/{\mathcal{F}}]$](img37.png) has canonical singularities. Up to an additional
small error,
has canonical singularities. Up to an additional
small error,
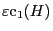 , for
, for
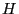 ample, and excluding the invariant curve
from factoring through a sub-variety
ample, and excluding the invariant curve
from factoring through a sub-variety
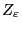 ,
,
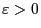 , the statement is exactly as
per (c), and is a theorem in all dimensions,
[M5] V.5, or [M4] §II.
, the statement is exactly as
per (c), and is a theorem in all dimensions,
[M5] V.5, or [M4] §II.
 (
( )
)
- Parenthesis: Duality. If one
is only interested in the hyperbolicity of surfaces this
step can be eschewed, but it would obscure the structure.
Exactly as in (d) for surfaces, should there be a
Zariski dense invariant
entire curve, or indeed un-bounded discs not
close to a sub-variety,
one finds an invariant measure
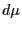 meeting
every effective Cartier divisor non-negatively,
and
meeting
every effective Cartier divisor non-negatively,
and
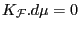 . By a theorem
of Bogomolov, [B2],
. By a theorem
of Bogomolov, [B2],
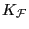 is either
big, or has numerical co-dimension 1. The
former would imply the absurdity that
is either
big, or has numerical co-dimension 1. The
former would imply the absurdity that 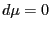 ,
so we may suppose the latter. Quite generally,
however, if
,
so we may suppose the latter. Quite generally,
however, if 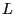 is a nef. bundle on a variety
of dimension
is a nef. bundle on a variety
of dimension 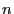 , of numerical dimension
, of numerical dimension
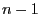 , then the only class in
, then the only class in
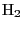 which meets every Cartier divisor non-negatively
and
which meets every Cartier divisor non-negatively
and 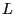 in 0 is
in 0 is 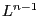 , [M6] II.2.
As such we may suppose that
, [M6] II.2.
As such we may suppose that
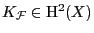 and
and
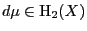 are in duality.
are in duality.
 (
(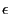 )
)
- Lemma 4: The Residue Lemma.
Exactly as per (e) the calculation of the intersection
of the invariant bundle
![$ K_{[X/\mathcal{F}]}$](img59.png) with
the invariant measure
with
the invariant measure 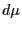 localises at the
singularities of the foliation,
localises at the
singularities of the foliation, 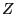 . However, this only means that
there is a 1-form
. However, this only means that
there is a 1-form 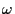 smooth off
smooth off 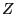 such that,
It has a priori absolutely nothing to do with
Cauchy residues, mixed Hodge theory, or, whatever.
It is, rather, one of several invariants which
control how far the term ``invariant measure''
may be un-ambiguously applied to
such that,
It has a priori absolutely nothing to do with
Cauchy residues, mixed Hodge theory, or, whatever.
It is, rather, one of several invariants which
control how far the term ``invariant measure''
may be un-ambiguously applied to 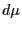 at the
singularities, and the Residue lemma, the most
important case of which is that encountered in (e),
asserts that this is controlled by the simplest
possible such invariant,
at the
singularities, and the Residue lemma, the most
important case of which is that encountered in (e),
asserts that this is controlled by the simplest
possible such invariant,
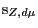 ,
the Segre class/Cauchy winding number of
,
the Segre class/Cauchy winding number of
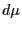 around
around 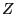 . The matter is explained in
detail in the introduction to [M7],
which is the proof of the lemma in dimension 3.
Philosophically, op. cit. is a huge advance on
previous efforts to prove the residue lemma
since it introduces a new idea, almost holonomy,
which allows one to exploit the measure regularity
(without which the residue lemma is wholly false) without
knowing anything about the relation between the
formal and analytic structure of the singularities,
which is just as well, since already in dimension 3
this is far too complicated, [MP2],
to have any relevance to this problem. Nevertheless,
the application of this idea in [M7]
makes extensive use of dimension 3, so, here,
much more so than for resolution of singularities,
there is still work to be done.
. The matter is explained in
detail in the introduction to [M7],
which is the proof of the lemma in dimension 3.
Philosophically, op. cit. is a huge advance on
previous efforts to prove the residue lemma
since it introduces a new idea, almost holonomy,
which allows one to exploit the measure regularity
(without which the residue lemma is wholly false) without
knowing anything about the relation between the
formal and analytic structure of the singularities,
which is just as well, since already in dimension 3
this is far too complicated, [MP2],
to have any relevance to this problem. Nevertheless,
the application of this idea in [M7]
makes extensive use of dimension 3, so, here,
much more so than for resolution of singularities,
there is still work to be done.
 (
(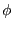 )
)
- Final Assembly: By Induction on dimension
For
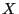 of dimension
of dimension 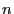 the hypothesis of (f) become
that at least one of
the hypothesis of (f) become
that at least one of
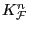 ,
,
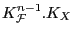 is non-zero. These hypothesis are, of course, satisfied
when the foliation comes from an order
is non-zero. These hypothesis are, of course, satisfied
when the foliation comes from an order 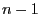 O.D.E.
on an algebraic surface, and, as we've noted, the
former trivially implies by (
O.D.E.
on an algebraic surface, and, as we've noted, the
former trivially implies by (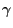 ) that
there cannot be a Zariski
dense invariant entire curve, or families of unbounded invariant
discs that are not close to an algebraic
sub-variety. Thus we're in the latter case,
and we reason exactly as per (f), but now by
way of the higher dimensional (
) that
there cannot be a Zariski
dense invariant entire curve, or families of unbounded invariant
discs that are not close to an algebraic
sub-variety. Thus we're in the latter case,
and we reason exactly as per (f), but now by
way of the higher dimensional (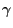 ),
and (
),
and (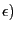 ) rather than (d) and (e),
to deduce that the Segre class
) rather than (d) and (e),
to deduce that the Segre class
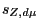 around the singular locus
around the singular locus 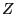 is non-zero.
Now, this is not an easy thing to happen
for a closed positive
current,
is non-zero.
Now, this is not an easy thing to happen
for a closed positive
current, 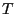 , let alone an invariant measure.
Indeed quite generally, by way of counting
sections of a small perturbation by an ample: if
, let alone an invariant measure.
Indeed quite generally, by way of counting
sections of a small perturbation by an ample: if 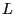 is nef., of numerical dimension
is nef., of numerical dimension 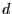 ,
, 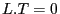 , and
, and
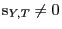 for
for 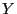 of dimension
less than
of dimension
less than 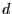 then
then 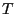 is supported in a
countable union of proper algebraic sub-varieties.
Given the minimal model theorem (
is supported in a
countable union of proper algebraic sub-varieties.
Given the minimal model theorem (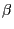 ) this is as
near to a reduction of dimension as makes no
difference. For foliations coming from O.D.E.'s
on an algebraic surface
) this is as
near to a reduction of dimension as makes no
difference. For foliations coming from O.D.E.'s
on an algebraic surface 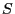 , the details of the induction
are in [M6], and we conclude that
, the details of the induction
are in [M6], and we conclude that 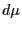 pushes forward to a countable sum of rational
and elliptic curves on
pushes forward to a countable sum of rational
and elliptic curves on 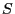 . So, certainly, the
surface is hyperbolic iff it contains no
rational or elliptic curves. To do better appears
to require the construction of foliated flops,
which, in one of life's ironies, is more
difficult than the construction of flips
in (
. So, certainly, the
surface is hyperbolic iff it contains no
rational or elliptic curves. To do better appears
to require the construction of foliated flops,
which, in one of life's ironies, is more
difficult than the construction of flips
in (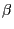 ). A weak form of the termination
of flops in dimension 3 is proved in [M6],
and this allows one to conclude that the
sum is finite. The impossibility of a finite
sum, however, has been established in [M4] III.4,
and whence for 2nd order O.D.E.'s on algebraic
surfaces one has a serious of results which
are best possible as explained in no. 1-5
of the F.A.Q..
). A weak form of the termination
of flops in dimension 3 is proved in [M6],
and this allows one to conclude that the
sum is finite. The impossibility of a finite
sum, however, has been established in [M4] III.4,
and whence for 2nd order O.D.E.'s on algebraic
surfaces one has a serious of results which
are best possible as explained in no. 1-5
of the F.A.Q..
home
Michael McQuillan, 15/07/2012
![]() on algebraic
surfaces, where, strictly speaking, around
the singularities the champ classifiant
on algebraic
surfaces, where, strictly speaking, around
the singularities the champ classifiant
![]() is purely notational,
and, otherwise as per [SGA.I] exposé VI.
The general case of the conjecture
was reduced by Green & Griffiths, [GG], to
entire curves satisfying a
is purely notational,
and, otherwise as per [SGA.I] exposé VI.
The general case of the conjecture
was reduced by Green & Griffiths, [GG], to
entire curves satisfying a ![]() dimensional
order O.D.E.,
dimensional
order O.D.E.,
![]() , on an algebraic
surface, so, in particular a Zariski dense
entire curve invariant by a foliation by
curves on a variety of dimension
, on an algebraic
surface, so, in particular a Zariski dense
entire curve invariant by a foliation by
curves on a variety of dimension ![]() .
As such the basic strategy is to make
this key point in the classification
theory of foliations work in all dimensions.
It now fits into a general structure, and
may be succinctly summarised,
.
As such the basic strategy is to make
this key point in the classification
theory of foliations work in all dimensions.
It now fits into a general structure, and
may be succinctly summarised,
![]() .
As has been said,
Green & Griffiths themselves, [GG],
established the reduction of their
conjecture for surfaces to the study
of foliations by curves on higher
dimensional varieties. The
dimension in question being limited
as a function of the ratio of
.
As has been said,
Green & Griffiths themselves, [GG],
established the reduction of their
conjecture for surfaces to the study
of foliations by curves on higher
dimensional varieties. The
dimension in question being limited
as a function of the ratio of
![]() to
to
![]() . Close to
the Castelnuovo line, the dimension
is potentially so large as to have
the same practical effect as being
arbitrary. As such, we need to understand
the above schema
for a foliation
. Close to
the Castelnuovo line, the dimension
is potentially so large as to have
the same practical effect as being
arbitrary. As such, we need to understand
the above schema
for a foliation
![]() by curves
in arbitrary dimension, viz:
by curves
in arbitrary dimension, viz:
![$\displaystyle K_{[X/\mathcal{F}]}.d\mu=\lim_{\varepsilon\rightarrow 0}
\int_{\mathrm{dist}_Z=\varepsilon} \omega d\mu$](img61.png)