It is a theorem that for algebraic surfaces ![]() of
general type with
enough two jets, e.g.
of
general type with
enough two jets, e.g.
![]() .
More precisely, on such surfaces:
the rational and elliptic curves form a closed proper
sub-variety
.
More precisely, on such surfaces:
the rational and elliptic curves form a closed proper
sub-variety ![]() of
of ![]() and any entire map
and any entire map
![]() factors through
factors through ![]() .
.
Indeed there are. Notations as above, with
![]() ample on
ample on ![]() then there
is a constant
then there
is a constant
![]() such that for
such that for
![]() any map from a parabolic (in the
sense of Ahlfors) Riemann surface not factoring through
any map from a parabolic (in the
sense of Ahlfors) Riemann surface not factoring through ![]() ,
,
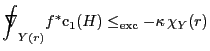
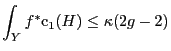
Again, same class of surfaces, same notation,
a sequence of discs
![]() which is
not contained in arbitrarily small neighbourhoods
of
which is
not contained in arbitrarily small neighbourhoods
of ![]() has a convergent subsequence which
converges to a disc with bubbles. The behaviour
around
has a convergent subsequence which
converges to a disc with bubbles. The behaviour
around ![]() may also be quantified optimally
in terms of the degeneracy of the Kobayashi metric-
basically exactly the reciprocal of the distance
to
may also be quantified optimally
in terms of the degeneracy of the Kobayashi metric-
basically exactly the reciprocal of the distance
to ![]() . This is a wholly general corollary
for surfaces which settles a question I posed
at the Peking I.C.M., [M3] 3.1. It follows
from a theorem of
Duval, [D], and [M4], but,
since the former post dates the latter,
the proof cannot be found in the downloads
section.
For the moment, therefore, exercise for the
reader, though probably worth a stand alone version.
. This is a wholly general corollary
for surfaces which settles a question I posed
at the Peking I.C.M., [M3] 3.1. It follows
from a theorem of
Duval, [D], and [M4], but,
since the former post dates the latter,
the proof cannot be found in the downloads
section.
For the moment, therefore, exercise for the
reader, though probably worth a stand alone version.
Better again. It's immediate whether by the above theorem of Duval, [D], or another of Kleiner, [K], that Gromov's isoperimetric inequality holds.
Not at all, there are log, stack, and log-stack versions of all of the above. The only thing that is required is the 2-jet condition. Most of the changes in the statements are the obvious, while 4 holds in the log case with respect to a complete distance, which is about the only point that requires extra work.
Quite a few,
- (a)
- Resolution of foliation singularities
for 3-folds, [MP1].
- (b)
- Minimal models for foliations by curves,
[M5], i.e. the canonical
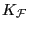 along
the foliation
along
the foliation
![$ X\rightarrow [X/\mathcal{F}]$](img16.png) with canonical
(foliation) singularities is nef. if the foliation
isn't in conics.
with canonical
(foliation) singularities is nef. if the foliation
isn't in conics.
- (c)
- What's termed a refined tautological
inequality, basically:
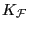 measures curvature
iff the singularities are canonical, [M5] V.5,
or [M4] §II.
measures curvature
iff the singularities are canonical, [M5] V.5,
or [M4] §II.
- (d)
- The residue lemma, [M8]. This forces the
intersection of
![$ K_{[X/\mathcal{F}]}$](img17.png) with an invariant
measure
with an invariant
measure 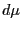 to be zero, when, functorially understood,
the measure has zero winding number/Segre class
to be zero, when, functorially understood,
the measure has zero winding number/Segre class
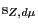 around the
foliation singularities.
around the
foliation singularities.
It goes as follows: standard results about
existence of jets on surfaces tell us that
if anything in nos. 1 or 2 is false, we can find a
foliation by curves
![]() on a variety of dimension
on a variety of dimension
![]() (bounded at worst in terms of the chern numbers) leaving
the curves in question invariant. Sub-sequencing
appropriately, and taking the dimension of
(bounded at worst in terms of the chern numbers) leaving
the curves in question invariant. Sub-sequencing
appropriately, and taking the dimension of ![]() to be minimal, this gives an invariant measure
to be minimal, this gives an invariant measure
![]() intersecting every effective divisor non-negatively.
By (c),
intersecting every effective divisor non-negatively.
By (c),
![]() , so by (b)
, so by (b)
![]() ,
and, we have
,
and, we have
![]() parallel to
parallel to ![]() in homology.
The residue lemma implies, however, that if
in homology.
The residue lemma implies, however, that if ![]() is the singular locus of the foliation then
is the singular locus of the foliation then
![]() , which for a closed positive
current,
, which for a closed positive
current, ![]() , let alone an invariant measure is not
easy, i.e.
, let alone an invariant measure is not
easy, i.e. ![]() ,
, ![]() nef of numerical Kodaira
dimension
nef of numerical Kodaira
dimension ![]() ,
,
![]() for
for ![]() of dimension
less than
of dimension
less than ![]() implies
implies ![]() is supported in a
countable union of proper algebraic sub-varieties.
Given the minimal model theorem (c) this is as
near to a reduction of dimension as makes no
difference. For a more detailed
explanation go to the overview of the proof.
is supported in a
countable union of proper algebraic sub-varieties.
Given the minimal model theorem (c) this is as
near to a reduction of dimension as makes no
difference. For a more detailed
explanation go to the overview of the proof.
As is explained in the overview of the proof, the chain of reasoning is indeed valid, but critically 6 (a) & (d) have, so far, only been proved in dimension 3. Otherwise (b) holds in all dimensions starting from a model with canonical singularities, and (c) holds unconditionally.
Evidently we'd need restrictions on the
chern numbers to reduce to foliations
by curves, e.g.
![]() semi-positive,
semi-positive,
![]() might work. However,
even then the resulting canonical along
the foliation
might work. However,
even then the resulting canonical along
the foliation
![]() can have numerical
Kodaira dimension 1, e.g. a tri-disc
quotient, so one needs a better residue
lemma. This is on the to do list, since
it's the principle missing fact to get
a classification theorem for foliations
by curves on 3-folds, i.e. currently
there isn't enough machinery to cover
(foliated) numerical Kodaira dimension 1
in dimension 3. Nevertheless, I wholly
expect not only the Green-Griffiths
conjecture whenever the chern numbers
of the 3-fold
permit a reduction to foliation by curves,
but a full classification theorem à
la [M2] of foliations by curves
on projective 3-folds. If, however, one
only had a reduction to foliations by
surfaces, or similar, then looking for
a counter example may easily be the
better strategy. After all, cf. no. 11,
the ``Green-Griffiths conjecture'' is
already false for schemes of dimension 3
in mixed characteristic.
can have numerical
Kodaira dimension 1, e.g. a tri-disc
quotient, so one needs a better residue
lemma. This is on the to do list, since
it's the principle missing fact to get
a classification theorem for foliations
by curves on 3-folds, i.e. currently
there isn't enough machinery to cover
(foliated) numerical Kodaira dimension 1
in dimension 3. Nevertheless, I wholly
expect not only the Green-Griffiths
conjecture whenever the chern numbers
of the 3-fold
permit a reduction to foliation by curves,
but a full classification theorem à
la [M2] of foliations by curves
on projective 3-folds. If, however, one
only had a reduction to foliations by
surfaces, or similar, then looking for
a counter example may easily be the
better strategy. After all, cf. no. 11,
the ``Green-Griffiths conjecture'' is
already false for schemes of dimension 3
in mixed characteristic.
This is a common misunderstanding resulting from
a lack of knowledge as to the logical limitations of what
is actually possible. The above assertion is
true, and a theorem of Steven Lu, [L], for surfaces of general type whenever
![]() . Otherwise,
by way of (an introductory) illustration consider what
happens on the line
. Otherwise,
by way of (an introductory) illustration consider what
happens on the line
![]() ,
where we have the following statements:
,
where we have the following statements:
(A) Let ![]() be a surface of general
type with
be a surface of general
type with
![]() , then there are
constants
, then there are
constants ![]() depending only on
depending only on
![]() and
and
![]() such that for any curve
such that for any curve ![]() on
on ![]() ,
,
(B) There are infinitely many surfaces
![]() on the line
on the line
![]() such that for
such that for ![]() with probability
with probability ![]() ,
, ![]() modulo
modulo ![]() has a
rational curve of degree
has a
rational curve of degree ![]() .
.
Now (B) is true, so it follows that while true in characteristic
zero, (A) is false in mixed characteristic,
even for the weaker statement that ![]() are
simply bounded uniformly in
are
simply bounded uniformly in ![]() . Whence,
. Whence,
(C) Fact There is no theorem which is
valid for ![]() , e.g. an
, e.g. an
![]() theorem,
which together with the inequality,
theorem,
which together with the inequality,
This particular example can be understood
in terms of smooth foliations on surfaces
so all the steps (a)-(f)
in the main strategy in characteristic zero are pretty trivial,
and one knows that the surfaces giving rise
to (B) are (non-integrable) bi-disc quotients.
In mixed characteristic (b)
fails, but not in an important way.
Interestingly, an appropriate version
of (c)
holds, [M9], so for ![]() ample one can use
duality to get on a bi-disc quotient
ample one can use
duality to get on a bi-disc quotient ![]() , a class
, a class ![]() in
in
![]() , in characteristic zero,
such that,
, in characteristic zero,
such that,
- (i)
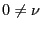 is nef., i.e. intersects
every Cartier divisor non-negatively.
is nef., i.e. intersects
every Cartier divisor non-negatively.
- (ii)
- There is a sequence (Zariski dense in
the ambient 3 -dimensional scheme) of rational curves
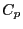 (actually components of the locus of
super singular abelian surfaces in terms
of the modular description of
(actually components of the locus of
super singular abelian surfaces in terms
of the modular description of 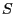 )
for
)
for 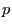 running through about half the primes,
such that for any divisor
running through about half the primes,
such that for any divisor 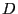 , in characteristic zero,
and the specialisation
, in characteristic zero,
and the specialisation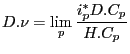
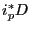 is understood
only to have sense for
is understood
only to have sense for 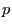 sufficiently large.
sufficiently large.
- (iii)
- For
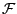 whichever of the
foliations on the bi-disc quotient one pleases,
we may suppose that the
whichever of the
foliations on the bi-disc quotient one pleases,
we may suppose that the 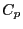 are
are
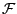 invariant, and,
invariant, and,
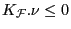
At this point the reasoning (d)
is wholly valid, and we conclude that ![]() is parallel to
is parallel to
![]() in Néron-Severi
in characteristic zero. The
residue lemma, however, fails, albeit
not by that much since it does have
variants in characteristic
in Néron-Severi
in characteristic zero. The
residue lemma, however, fails, albeit
not by that much since it does have
variants in characteristic ![]() , which
since these foliations are smooth amounts to,
, which
since these foliations are smooth amounts to,
ZFC or similar could be inconsistent, but
an inconsistency at this level is enormously
improbable. In addition the residue theorem
for smooth foliations is trivial and purely
algebraic as far as algebraic curves are
concerned. As to Miyaoka's proof it needs
closedness of differential forms. The forms
in question are different for every curve
of which one wants to bound the degree.
Similarly, in the context of (A), Bogomolov's
proof needs the Frobenius theorem, which in
the example in question is true at exactly
the primes where one does not find
the ![]() appearing in no. 10, while in
a more general situation it uses Jordan
decomposition for log-canonical singularities,
which although valid in characteristic
appearing in no. 10, while in
a more general situation it uses Jordan
decomposition for log-canonical singularities,
which although valid in characteristic ![]() is much less useful. Thus, Bogomolov's proof is
a variant on the residue lemma, actually a
less algebraic one in the context of algebraic curves, while
Miyaoka's uses properties of differentiation
in characteristic zero that could be considered
even less algebraic again, so, in all cases,
there's no inconsistency, and there's nothing
to see here, move along.
is much less useful. Thus, Bogomolov's proof is
a variant on the residue lemma, actually a
less algebraic one in the context of algebraic curves, while
Miyaoka's uses properties of differentiation
in characteristic zero that could be considered
even less algebraic again, so, in all cases,
there's no inconsistency, and there's nothing
to see here, move along.
Quite true, and Lu did exactly this,
but it only works because one is on
the line
![]() . However,
under the line,
one can make much more
difficult variants on the above
by taking bi-disc quotients with cusps.
So in the
region
. However,
under the line,
one can make much more
difficult variants on the above
by taking bi-disc quotients with cusps.
So in the
region
![]() for any
for any
![]() ,
as many examples as one pleases, with the
structure of the rational curves in mixed
characteristic exactly as in no. 10. As
such we can radically extend the surfaces
to which Fact (C) of no. 10 applies, and
all of (i)-(iii) hold too, but there is
no hope of detecting from stability considerations
that one is looking
at such an example unless one can find the
cusps first. Such examples also
have serious practical consequences,
e.g. in the jet bundle
of order
,
as many examples as one pleases, with the
structure of the rational curves in mixed
characteristic exactly as in no. 10. As
such we can radically extend the surfaces
to which Fact (C) of no. 10 applies, and
all of (i)-(iii) hold too, but there is
no hope of detecting from stability considerations
that one is looking
at such an example unless one can find the
cusps first. Such examples also
have serious practical consequences,
e.g. in the jet bundle
of order ![]() the natural foliations on the bi-disc
define surfaces
the natural foliations on the bi-disc
define surfaces ![]() - actually the
blow up
- actually the
blow up ![]() -times in the singularities
of the cusps- and the restriction of the
-times in the singularities
of the cusps- and the restriction of the
![]() th tautological bundle
th tautological bundle ![]() has the
form
has the
form
![]() where
where
![]() is the exceptional divisor arising
from
the
is the exceptional divisor arising
from
the ![]() th blow up. Now
th blow up. Now
![]() is nef. of numerical Kodaira dimension 1,
but Kodaira dimension
is nef. of numerical Kodaira dimension 1,
but Kodaira dimension ![]() , thus,
no matter what jet space one looks in
, thus,
no matter what jet space one looks in
![]() isn't even pseudo effective. As
such even formulating
an Ahlfors-Schwarz lemma here, as
opposed to its functorial cousin,
the tautological inequality,
(c),
is very demanding.
Of course, one could attempt a highly
degenerate pseudo-metric formulation
of Ahlfors-Schwarz, but the technical
problems are legion, and very similar to
those encountered in the classification
theorem as described in no. 13 below.
Finally, all of this
is under the best possible hypothesis
that one is looking at a model with
canonical singularities, since otherwise
were there to be a model of such an
example such that
isn't even pseudo effective. As
such even formulating
an Ahlfors-Schwarz lemma here, as
opposed to its functorial cousin,
the tautological inequality,
(c),
is very demanding.
Of course, one could attempt a highly
degenerate pseudo-metric formulation
of Ahlfors-Schwarz, but the technical
problems are legion, and very similar to
those encountered in the classification
theorem as described in no. 13 below.
Finally, all of this
is under the best possible hypothesis
that one is looking at a model with
canonical singularities, since otherwise
were there to be a model of such an
example such that
![]() had
sections, then it would be decidedly a case of
barking up the wrong tree.
had
sections, then it would be decidedly a case of
barking up the wrong tree.
It is true that bi-disc quotients, both
integrable and non-integrable are the
only such examples. Both have numerical
Kodaira dimension 1, which is also the
Kodaira dimension of the former, but,
as we've said, the latter is ![]() .
As to the rest of the question this was
the original motivation for
the classification theorem, [M2],
since it was clear even then that the residue lemma
in arbitrary dimension would not be easy.
The subject is dealt with at length in
the introduction to op. cit., but briefly:
one gets very close to proving the
classification theorem without recourse
to [M1], and what is required
is a sufficiently regular psh. metricisation
of
.
As to the rest of the question this was
the original motivation for
the classification theorem, [M2],
since it was clear even then that the residue lemma
in arbitrary dimension would not be easy.
The subject is dealt with at length in
the introduction to op. cit., but briefly:
one gets very close to proving the
classification theorem without recourse
to [M1], and what is required
is a sufficiently regular psh. metricisation
of
![]() in the nef. Kodaira
dimension
in the nef. Kodaira
dimension ![]() case. However I couldn't
find such a thing, and Marco Brunella
changed the logic. More precisely, one knows from [M1]
that in this case the Poincaré metric along
the leaves vanishes only on an algebraic
set (so, post factum the cusps in no. 12).
A priori it may not be psh., but Brunella
proved that it was (a result he subsequently
generalised to all dimensions),
and I kicked
the ball over the line by showing that
it was also continuous. This gave a metric
of the desired regularity, and solved
the outstanding issue in the classification
theorem, but it completely inverted the
intended logic by deducing the classification
theorem from [M1] rather than re-proving
it as was intended. I couldn't say with logical
certainty that this is the only way to proceed-
there is some discussion of a characteristic
case. However I couldn't
find such a thing, and Marco Brunella
changed the logic. More precisely, one knows from [M1]
that in this case the Poincaré metric along
the leaves vanishes only on an algebraic
set (so, post factum the cusps in no. 12).
A priori it may not be psh., but Brunella
proved that it was (a result he subsequently
generalised to all dimensions),
and I kicked
the ball over the line by showing that
it was also continuous. This gave a metric
of the desired regularity, and solved
the outstanding issue in the classification
theorem, but it completely inverted the
intended logic by deducing the classification
theorem from [M1] rather than re-proving
it as was intended. I couldn't say with logical
certainty that this is the only way to proceed-
there is some discussion of a characteristic ![]() alternative in
[M2]- but
I'd be very surprised if either Brunella's inversion
of the logic isn't dictated by the nature of
the problem or there were a
substantially different strategy in
characteristic 0 which escapes the
logical loop that it creates.
alternative in
[M2]- but
I'd be very surprised if either Brunella's inversion
of the logic isn't dictated by the nature of
the problem or there were a
substantially different strategy in
characteristic 0 which escapes the
logical loop that it creates.
Mihai Paun pointed out around may 2005 that
IV.7.3 in [M6] is wrong. This amounted
exactly to a mistake in the proof of the
residue lemma- basically the plan was to
do some harmonic theory along the foliation,
and practically everything in [M6]
permits blowing up ad nauseum, but not
when doing the said harmonic theory.
This was corrected
in [M6.bis] a few months later. To achieve
the correction, however, it was necessary to
suppose more than just resolution of singularities,
denoted LCR, i.e. a stronger variant,
![]() , in
which the formal centre manifold converged in
dimension 3 in much the same way that it does
for 2 dimensional saddles. This was the
motivation for [MP2], which
proved something very close to
, in
which the formal centre manifold converged in
dimension 3 in much the same way that it does
for 2 dimensional saddles. This was the
motivation for [MP2], which
proved something very close to
![]() , but also
discovered that the precise form of
, but also
discovered that the precise form of
![]() hypothesised
[M6.bis] does not hold.
hypothesised
[M6.bis] does not hold.
No. The method of [M8] is completely new and has nothing to do with previous efforts to prove the residue lemma in [M6] and [M6.bis]. As is explained in the introduction to [M8], not withstanding the need for measure regularity in the residue lemma, it nevertheless achieves the calculation as a pure consequence of the formal structure around the singularities guaranteed by the resolution theorem [MP1]. As such [MP1], a.k.a. 6(a), a.k.a. LCR, is what is not only relevant, but a sine qua non.
In a strict logical sense that's correct, or, better the residue lemma can be proved without any reference to [MP2]. It has, however, been used occasionally for ease of exposition and avoiding repetition of very similar calculations. It is also essential reading if one really wants to understand what one is up against, and the problems that the new method of almost holonomy in [M8] has solved.
In effect, it can't, one has to work with
continuous functions. The appendix was
there since it was used in the proof of
residue lemma conditional on
![]() ,
cf. no. 14. Since the proof of the residue
lemma is now what it should be, i.e.
relies only on LCR, this section no longer
has any logical relevance to the proof.
Nevertheless, it is pretty interesting, and
even more so when one replaces Borel by
continuous. There'll be a stand alone
version shortly, [M10].
,
cf. no. 14. Since the proof of the residue
lemma is now what it should be, i.e.
relies only on LCR, this section no longer
has any logical relevance to the proof.
Nevertheless, it is pretty interesting, and
even more so when one replaces Borel by
continuous. There'll be a stand alone
version shortly, [M10].
Basically No. Obviously more polished versions are
going to be ready sooner rather than
later, but the basic rule with the current
versions is just ignore everything that
either [M6] or [M6.bis] says
about the residue lemma, except the
final statement, and defer to [M8]
for the proof in dimension 3.
As such, even though for example
[M6.bis] IV.2.4 is wrong, and
the use of Stokes' in IV.6.7 may
not be justifiable without full
convergence of the centre manifold
relative to the measure, it's
wholly irrelevant, and the whole
of §IV be it of [M6] or [M6.bis]
should just be ignored. There will shortly
be a new version in which this section
will simply be cut.
Further technical
precisions: Sibony pointed out that
there are examples which oblige the use of
``a'', as opposed to ``the'', Segre class,
while Rousseau observed that the idea
behind [M6.bis] VI.1.5 is correct,
but the execution is wrong, so ![]() should be replaced by
should be replaced by ![]() , or thereabouts.
None of which has any adverse consequences
in practice beyond replacing
, or thereabouts.
None of which has any adverse consequences
in practice beyond replacing ![]() by
by
![]() in the 2-jet condition.
in the 2-jet condition.
If by arithmetic one means over
![]() then I'd say next to none. One needs to be
able to differentiate, although the need
for close to arbitrary dimension near the
Castelnuovo line, and the need for arbitrarily
many factors to get
then I'd say next to none. One needs to be
able to differentiate, although the need
for close to arbitrary dimension near the
Castelnuovo line, and the need for arbitrarily
many factors to get
![]() in Roth's
theorem are curiously reminiscent. Function
field arithmetic in characteristic 0 is
another matter, however, and in principle
[M7] §I solves the differentiation
problem, and the
basic strategy
should bound
the degree of rational points.
However, in the presence of bad reduction there's an issue that
I haven't been able to get to the bottom of,
so the best so far is Mordellicity for surfaces
with
in Roth's
theorem are curiously reminiscent. Function
field arithmetic in characteristic 0 is
another matter, however, and in principle
[M7] §I solves the differentiation
problem, and the
basic strategy
should bound
the degree of rational points.
However, in the presence of bad reduction there's an issue that
I haven't been able to get to the bottom of,
so the best so far is Mordellicity for surfaces
with
![]() which
relies on ideas from classification, but
differentiates in the classical way,
[M7] §2.
which
relies on ideas from classification, but
differentiates in the classical way,
[M7] §2.
Coincidentally there has been a significant revision of resolution of singularities in dimension 3, [MP1.bis]. As for updates in general, however, there are two problems: cookies on facebook and twitter which makes their use a non-starter, and, even were it otherwise, the rule in mathematics is whatever estimate you have for doing something, double it and move to the next unit of time, so, 1 hour becomes 2 days, 2 days 4 weeks, 4 weeks 8 months, etc.. As such, a dedicated twitter account rather than a home page may be an embrace too far of the interweb.
Mostly with latex2html on an OpenBSD-4.6 box after I edited the make file in the ports tree to compile against my teTeX installation as opposed to the TeX Live monster, although, curiously, it's not working as well on my 4.8 box. Irrespectively even on the 4.6 box it was making syntax errors in the internal linking, so I did that bit my hand. I'm impressed too.