INCA-ABACO: INfrastrutture di CAlcolo A BAsso COsto Utilizzo "banale" della programmazione parallela per effettuare un'analisi parametrica interessante: l'esempio delle sezioni di Poincaré per il modello di Hénon e Heiles.

1 Framework

1.1 Sezione di Poincaré

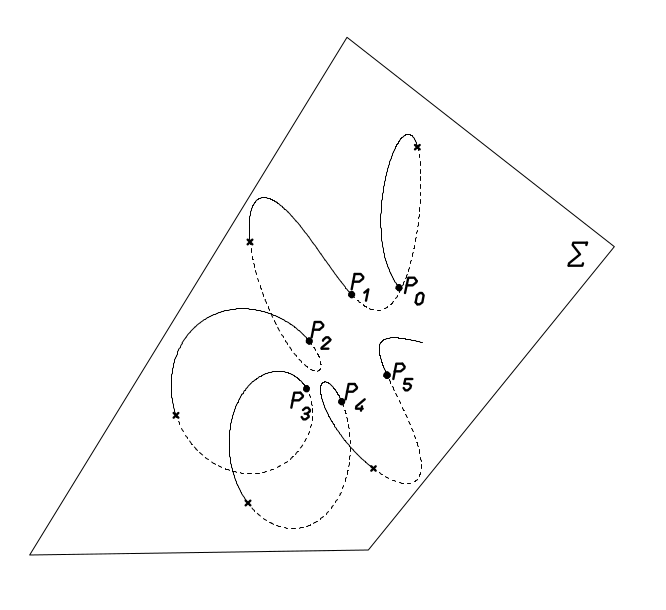
La sezione di Poincaré è un utile metodo per investigare le proprietà di un sistema dinamico. Sia data l’equazione differenziale autonoma in ℝⁿ

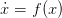
e sia Σ ⊂ ℝⁿ una ipersuperficie di dimensione n − 1 ortogonale al flusso Φ _t(x₀) con x₀ ∈ Σ condizione iniziale del sistema. Si definisce sezione di Poincaré l’applicazione

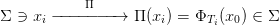
dove T_i è il tempo di ritorno i−esimo del flusso partito da x₀ (e.g. T₁ è il tempo del primo ritorno del flusso su Σ), con la condizione aggiuntiva che il verso della derivata ẋ(T_i) = f(x_i) è di segno concorde con quello iniziale ẋ(0) = f(x₀) rispetto alla normale all’ipersuperficie Σ.

1.2 Modello di Hénon e Heiles

Il modello di Hénon e Heiles è descritto dall’Hamiltoniana

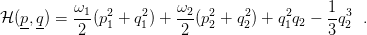
Siamo nel caso n = 4; fissando il valore dell’energia possiamo ottenere delle superfici di dimensione 3, al fine di studiare successivamente le sezioni di Poincaré del modello. Facciamo qualche osservazione sul comportamento di questo modello:

• per valori piccoli dell’energia, ∥q∥ ≪ 1, il sistema si comporta come una coppia di oscillatori armonici con frequenze ω₁ > 0, ω₂ > 0 con una piccola perturbazione costituita dai termini cubici;
• la superficie Σ individuata dall’equazione q₁ = 0 è trasversa al flusso se l’energia è positiva, come segue immediatamente dalle equazioni di Hamilton:

• fissato il valore E dell’energia, le intersezioni del flusso con la superficie Σ giacciono sul sottospazio bidimensionale dato dall’equazione

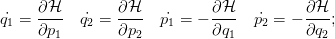
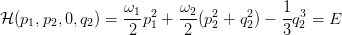
  e deduciamo che un punto (p₂,q₂) delle sezioni di Poincaré individua in modo univoco un’orbita dal momento che abbiamo q₁ = 0 e p₁ dato dall’equazione precedente assumendo che il segno sia positivo;

• il potenziale associato al modello è dato da

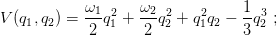
  lo studio di tale potenziale mostra che la sezione di Poincaré è limitata alla regione individuata dall’equazione

  

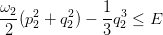
  purchè E sia minore della velocitè di fuga individuata da

  

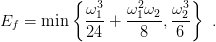
• il modello è un sistema reversibile, in quanto autonomo e pari nei momenti: infatti se (p(t),q(t)) è una soluzione, lo è anche la sua coniugata temporale data da ((t), (t)) = (−p(−t),q(−t)).

2 Simulazioni numeriche

Lo studio delle sezioni di Poincaré del modello è stato effettuato utilizzando un mini-cluster costituito da 15 Raspberry Pi, la cui descrizione dettagliata è disponibile alla corrispondente pagina web.

Utilizzando tale infrastruttura, è stato possibile eseguire in parallelo un programma scritto in linguaggio C, che calcola le sezioni di Poincaré per 15 valori diversi delle condizioni iniziali, a fissato livello di energia E = 0.039344. Il suddetto programma (che si chiama omp_henon-heiles-sez-poin.c), il file che definisce i valori di ω₁, ω₂ e delle condizioni iniziali, insieme a tutti gli script di comandi (i quali permettono di eseguire il programma in parallelo su tutti i Raspberry) sono stati archiviati e compressi nel file omp_henon-heiles.zip. Lo schema di esecuzione parallela sul mini-cluster è analogo a quello discusso nell’esempio banale, che è descritto in questa pagina web

L’algoritmo di integrazione utilizzato è il metodo SBAB3C introdotto da Laskar e Robutel in [5]. A sua volta il metodo SBAB3C puè essere visto come una evoluzione di quello del punto centrale, o Leap-Frog, che è accuratamente descritto in [3]. Le seguenti figure mostrano rispettivamente le condizioni iniziali del sistema su cui è stata fatta l’integrazione e le sezioni di Poincaré nello spazio delle fasi (q₂,p₂).

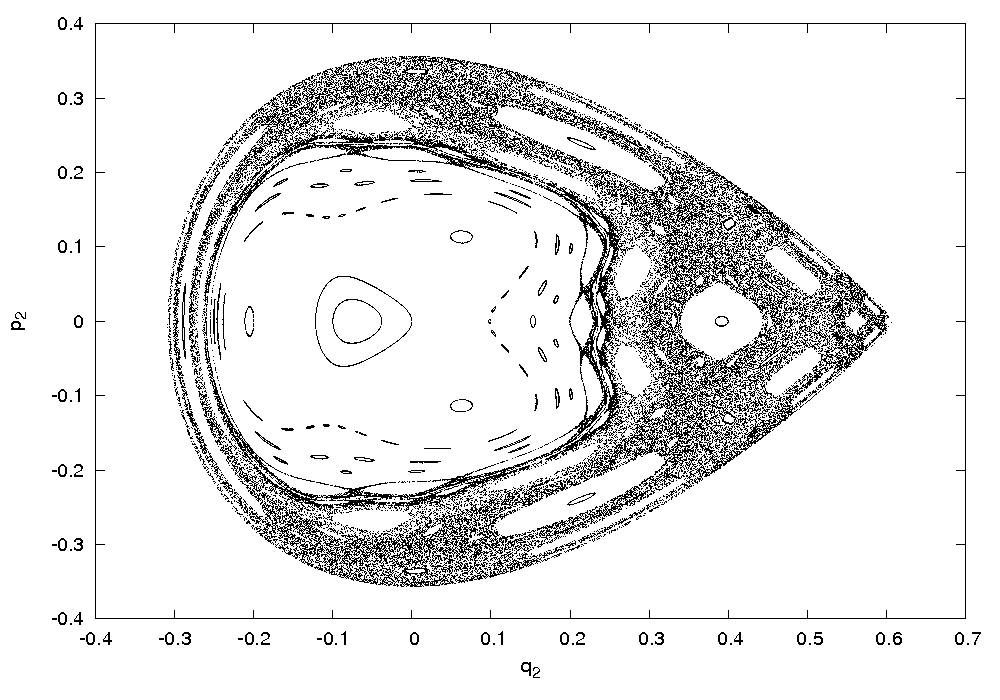
Figura 3: Sezione di Poincaré per il caso non risonante (ω₁ = 1 e ω₂ = ( − 1)∕2) del modello di Hénon e Heiles corrispondente al valore dell’energia E = 0.039344 , che è leggermente inferiore a quello di fuga.

3 Conclusioni

Il caso in esame, che è non risonante (cioè tale che ∄(k₁,k₂) ∈ ℤ² \ (0, 0) per cui si ha che k₁ω₁ + k₂ω₂ = 0), mostra una zona centrale con curve chiuse invarianti concentriche. Sono presenti delle zone in cui è possibile il moto ordinato su curve chiuse 1D che stanno intorno ad orbite periodiche. Tuttavia è molto ampia l’area della superficie che viene riempita in maniera apparentemente erratica e abbastanza uniforme dall’orbita che parte da un punto iniziale all’interno di quella stessa regione. Questo comportamento è tipico delle orbite caotiche (cfr. [2])

Lo scenario è quindi il medesimo rispetto a quello descritto, ad esempio, in [6], dove troviamo anche un’analisi per diversi livelli di energia e una breve discussione del caso risonante.

4 Breve analisi delle prestazioni del nostro mini-cluster

Per comprendere i vantaggi dell’uso del mini-cluster, il programma è stato eseguito anche su Marvin, cioè il server/workstation principale del nostro cluster. I tempi di esecuzione riportati nel seguito sono stati ottenuti utilizzando il comando time.

Per comprendere meglio le differenze tra i due apparati, è bene ricordare che il mini-cluster è composto da 15 Raspberry Pi 3, ciascuno equipaggiato con un processore quad-core da 1.2GHz a 64bit con architettura ARM, mentre Marvin monta un processore Intel i5 quad-core da 3.3 GHz a 64bit.

Il tempo che corrisponde al parametro real è il tempo totale per l’esecuzione del programma; in esso si tiene conto anche dei tempi di lettura e scrittura da file, nonché di quelli necessari al passaggio di informazioni tra Raspberry e Marvin; il "real time" dipende quindi anche dalla velocitè della rete locale. Lo "user time" fornisce invece il valore del tempo effettivo di utilizzo della CPU, così come richiesto dall'esecuzione dall'esecuzione del programma. Per maggiori dettagli sulle specifiche di questi tempi si rimanda ai manuali tecnici.

Per studiare al meglio i diversi comportamenti di Marvin e del mini-cluster il programma è stato eseguito prima per un tempo totale di integrazione numerica delle equazioni del moto T_F = 10⁵ e poi con T _F = 10⁶, essi corrispondono, rispettivamente, al tracciamento di circa 10 migliaia e 100 migliaia di punti per ciascuna delle sezioni di Poincaré.

Analizzando i tempi di esecuzione per T_F = 10⁵ si nota che il tempo totale di esecuzione (real) è maggiore per i Raspberry di circa 21 secondi. È molto interessante notare che su Marvin il tempo totale di esecuzione e il tempo effettivo di calcolo differiscono per meno di un secondo, mentre la differenza è molto più marcata per il mini-cluster. Il fatto che il tempo complessivo (real) di esecuzione sia maggiore per i Raspberry è quasi certamente dovuto alla necessità di inviare e ricevere le informazioni tramite rete locale, con il passaggio di numerosi file tra Marvin e i Raspberry. Quando il programma viene eseguito solo su Marvin non è necessario trasferire alcun file, con un evidente risparmio di tempo.
Per quanto riguarda il tempo effettivo di calcolo, il mini-cluster è in leggero vantaggio e se ne può concludere che la parallelizzazione del problema ottiene l’effetto sperato, cioè la riduzione del tempo di calcolo effettivo.

Il secondo test, effettuato con tempo di integrazione T_F = 10⁶, mette maggiormente in evidenza il vantaggio di utilizzare un mini-cluster per problemi come quello considerato, che ben si prestano alla parallelizzazione. Infatti in questo secondo test il mini-cluster batte Marvin sul tempo totale di esecuzione. Analizzando i tempi, complessivamente Marvin impiega ben 2 minuti e 19 secondi in più per completare l'esecuzione del programma; anche in questo caso quasi tutto il tempo è impiegato per effettuare i calcoli richiesti dal programma stesso. Il mini-cluster impiega circa 13 minuti per eseguire il programma, di cui circa 12 minuti sono dovuti al tempo di calcolo effettivo. Si osserva quindi che per problemi ben parallelizzabili e su tempi relativamente lunghi, il mini-cluster offre un certo vantaggio rispetto all’uso di una singola macchina, sebbene ben più potente, come Marvin.

A questa analisi sui tempi, si possono aggiungere alcune considerazioni sui costi dell’hardware: sia il prezzo di Marvin, che quello richiesto dal mini-cluster composto da 15 Raspberry, è stato di circa 900€. Chiaramente i costi possono variare a seconda del momento dell’acquisto, del rivenditore, dei componenti scelti e degli eventuali accessori. Per valutare l’economicità dei diversi apparati, è da non sottovalutare il fatto che ogni Raspberry fornisce una licenza gratuita del software Mathematica, che permette di effettuare il calcolo simbolico in modi che sarebbero assai costosi su un Personal Computer tradizionale.

Alla luce di queste considerazioni, la parallellizzazione su un mini-cluster si rivela particolarmente vantaggiosa rispetto all’uso di un solo computer, sebbene quest’ultimo sia molto più potente di ciascun Raspberry. In un futuro relativamente breve, ci si aspetta di poter ulteriormente esplorare questo aspetto, nell'ambito della simulazione numerica di problemi scientifici che richiedono una discreta potenza di calcolo.

Riferimenti bibliografici