$$$$

Esercizi - Settimana 8

Esercizio

Si trovino le eventuali estremi (massimi/minimi) delle funzioni seguenti, dicendo se sono estremi globali o locali.

1. $f(x)=x^4-4x^3-8x^2+5$
2. $g(x)=x^6-3x^4$

Soluzione

1. Notando che $f^{\prime }(x)=4x^3-12x^2-16x=4x(x^2-3x-4)$, $f$ è sempre derivabile ed ha punti stazionari $x=-1,0,4$. Poi $f^{″}(x)=12x^2-24x-16$; quindi

$$f^{″}(-1)=20>0,f^{″}(0)=-16<0,f^{″}(4)=80>0$$

allora $-1$ e $-4$ sono minimi locali di $f$ e $0$ è un massimo locale. Per stabilire quali sono anche estremi globali, prima nota che

$$\underset{x\to \pm \mathrm{\infty }}{lim}f(x)=+\mathrm{\infty },$$

allora $f$ non ha nessun massimo locale. Per quanto riguarda i minimi, valutiamo

$$f(-1)=-5,f(4)=-130;$$

quindi $4$ è un minimo globale, $-1$ no. Riassumendo,

$$\boxed{{\displaystyle \text{Massimo locale in }0;\text{ minimo locale in }-1;\text{ minimo globale in }4}}.$$

(strettamente parlando anche $4$ è anche un minimo locale ma va bene lasciare intendere questo). b. Essendo $g^{\prime }(x)=6x^5-12x^3=6x^3(x^2-2)$, $g$ ha punti stazionari in $x=-\sqrt{2},0,\sqrt{2}$. Il segno di $g^{\prime }$ cambia così:

$$\begin{array}{ccccc}x& (-\mathrm{\infty },-\sqrt{2})& (-\sqrt{2},0)& (0,\sqrt{2})& (\sqrt{2},\mathrm{\infty })\\ g^{\prime }(x)& -& +& -& +\end{array}$$

e allora $-\sqrt{2},\sqrt{2}$ sono minimi locali e $0$ è un massimo locale (nonostante che $g^{″}(0)=0$). Allora notando anche che $\underset{\pm \mathrm{\infty }}{lim}g(x)=\mathrm{\infty }$ e $g(-\sqrt{2})=g(\sqrt{2})=-4$:

$$\boxed{{\displaystyle \text{Massimo locale in }0;\text{ minimi globali in }-\sqrt{2},\sqrt{2}}}.$$

Esercizio

Sia

$$f(x)=\frac{x^3+2x-2}{x}.$$

1. Qual'è il dominio di $f$?
2. Che sono i limiti di $f$ agli estremi degli intervalli in cui è definito?
3. Quali sono i estremi di $f$? Per ognuno, specifica di quale tipo si tratta (massimo/minimo, locale/globale) e il valore associato di $f$.
4. Tracciare il grafico di $f$.

Soluzione

1. $f$ è definito per ogni $x$ tranne $0$, ovvero il suo dominio è $\boxed{{\displaystyle (-\mathrm{\infty },0)\cup (0,\mathrm{\infty })}}$.
2. $$\underset{x\to \pm \mathrm{\infty }}{lim}f(x)=\underset{x\to \pm \mathrm{\infty }}{lim}{x}^2=\boxed{{\displaystyle \pm \mathrm{\infty }}};$$

poi visto che il denominatore di $f(x)$ vale $-2$ in $x=0$,

$$\underset{x\to 0^{-}}{lim}f(x)=\underset{x\to 0^{-}}{lim}\frac{-2}{x}=\boxed{{\displaystyle \mathrm{\infty }}},\underset{x\to 0^{+}}{lim}f(x)=\underset{x\to 0^{+}}{lim}\frac{-2}{x}=\boxed{{\displaystyle -\mathrm{\infty }}}$$

3. $$f^{\prime }(x)=\frac{(3x^2+2)x-x^3+2x-2}{x^2}=\frac{2x^3+2}{x^2},$$

allora c'è un unico punto stazionario in $x=-1$, e nessun punto di non-derivabilità nel dominio. Evidentemente $f^{\prime }(x)<0$ se $x<-1$ e $f^{\prime }(x)>0$ se $x\in (-1,0)$, allora $f$ ha

$$\boxed{{\displaystyle \text{un minimo locale in }x=-1,f(-1)=5}}$$

(visto i limiti, è necessariamente solo un minimo locale). d.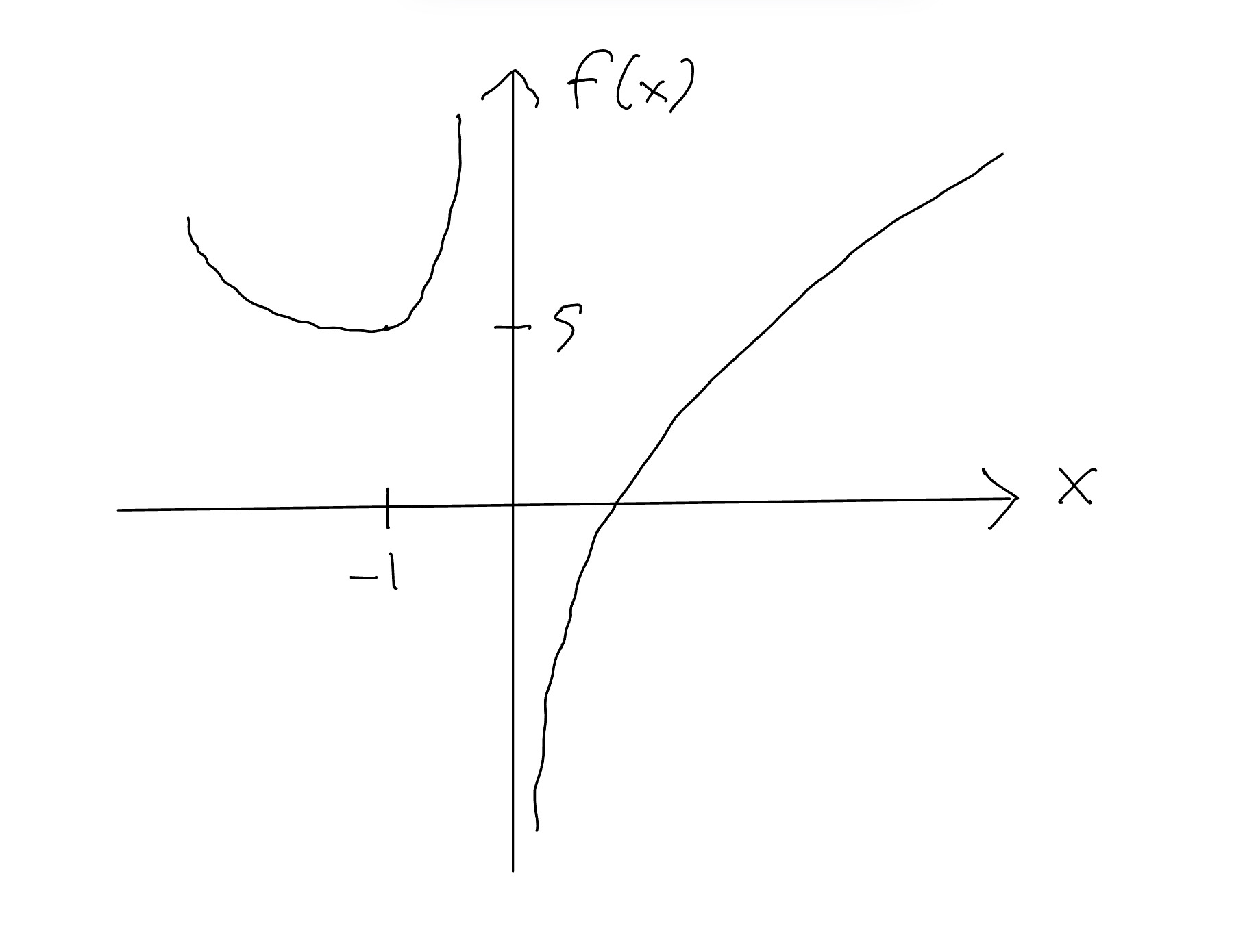

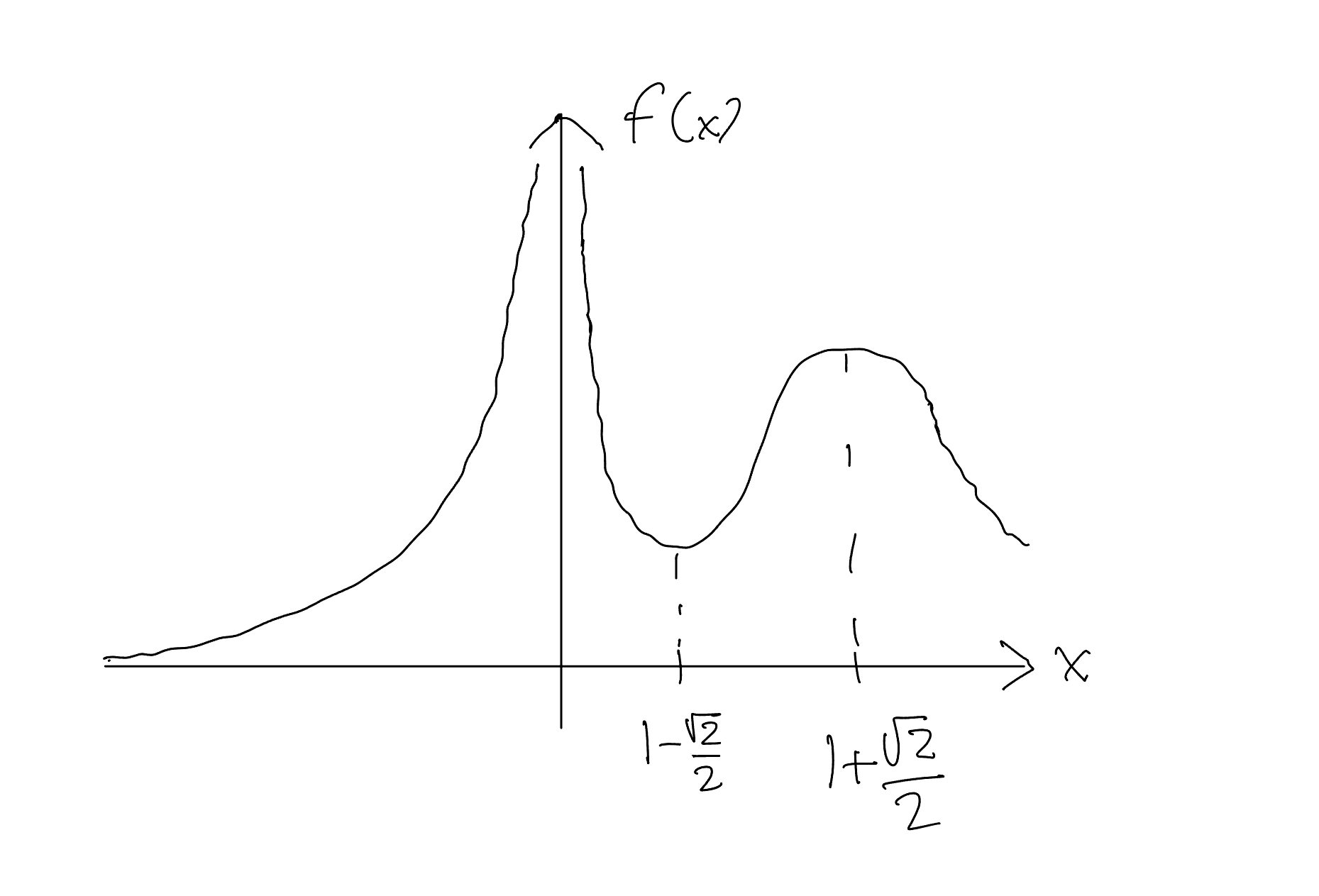
Esercizio

Sia

$$f(x)=\frac{e^{-(x-2{)}^2}}{|x|}.$$

1. Qual'è il dominio di $f$?
2. Che sono i limiti di $f$ agli estremi degli intervalli in cui è definito?
3. Quali sono i estremi di $f$? Per ognuno, specifica di quale tipo si tratta (massimo/minimo, locale/globale).
4. Tracciare il grafico di $f$.

Soluzione

È utile scrivere il valore assoluto per tratti,

$$f(x)=\{\begin{array}{ll}\frac{e^{-(x-2{)}^2}}{x},& x>0\\ -\frac{e^{-(x-2{)}^2}}{x},& x<0.\end{array}$$

1. $\boxed{{\displaystyle (-\mathrm{\infty },0)\cup (0,\mathrm{\infty })}}$
2. $\underset{\pm \mathrm{\infty }}{lim}f(x)=\boxed{{\displaystyle 0}}$, $\underset{x\to 0}{lim}f(x)=\underset{x\to 0}{lim}\frac{e^{-4}}{|x|}=\boxed{{\displaystyle \mathrm{\infty }}}$
3. Visto $\frac{d}{dx}[-(x-2{)}^2]=-2(x-2)$ ed allora $\frac{d}{dx}{e}^{-(x-2{)}^2}=-2(x-2)e^{-(x-2{)}^2}$,

$$f^{\prime }(x)=\{\begin{array}{ll}\frac{(-2(x-2)e^{-(x-2{)}^2})x-e^{-(x-2{)}^2}}{x^2},& x>0\\ -\frac{(-2(x-2)e^{-(x-2{)}^2})x-e^{-(x-2{)}^2}}{x^2},& x>0\end{array}=\{\begin{array}{ll}\frac{(-2x^2+4x-1)e^{-(x-2{)}^2}}{x^2},& x>0\\ -\frac{(-2x^2+4x-1)e^{-(x-2{)}^2}}{x^2},& x>0;\end{array}$$

i punti stazionari sono le soluzioni di $2x^2-4x+1=0$, ovvero $x=1\pm \sqrt{2}/2$, ambedue positivi, con valori positivi (quindi nessuno delle due un estrom globale, visto i limiti trovati sopra). Esaminando il segno di $f^{\prime }(x)$, $f$ ha

$$\boxed{{\displaystyle \text{un minimo locale in }x=1-\sqrt{2}/2,\text{ un massimo locale in }1+\sqrt{2}/2.}}$$

4. 

Esercizio

Calcolare i seguenti limiti:

1. $$\underset{x\to 0}{lim}\frac{1-\cos x}{x^2}$$
2. $$\underset{x\to 1}{lim}\frac{\sqrt{x+4}-2}{x}$$
3. $$\underset{x\to 2\pi }{lim}\frac{\exp (\cos x-1)-1}{{\sin }^{2}x}$$
4. $$\underset{x\to 1/2}{lim}\frac{1-2x+\ln (2x)}{1-4x+4x^2}$$
5. $$\underset{x\to 0^{+}}{lim}\frac{e^x-1}{x^2}$$

Soluzione

1. Applicando due volte la regola de l'Hôpital,

$$\underset{x\to 0}{lim}\frac{1-\cos x}{x^2}=\underset{x\to 0}{lim}\frac{\sin x}{2x}=\underset{x\to 0}{lim}\frac{\cos x}{2}=\boxed{{\displaystyle \frac{1}{2}}}.$$

2. $\underset{x\to 1}{lim}\frac{\sqrt{x+4}-2}{x}=\boxed{{\displaystyle \sqrt{5}-2}}$; nota che questo non è una forma indeterminata, quindi sarebbe incorretto applicare la regola de l'Hôpital in questo caso.
3. Usando $\frac{d}{dx}{e}^{\cos x-1}=-(\sin x)e^{\cos x-1}$ e la regola de l'Hôpital,

$$\begin{array}{rl}& \underset{x\to 2\pi }{lim}\frac{\exp (\cos x-1)-1}{{\sin }^{2}x}=\underset{x\to 2\pi }{lim}\frac{-(\sin x)\exp (\cos x-1)-1}{2\cos x\sin x}\\ & =-\underset{x\to 2\pi }{lim}\frac{\exp (\cos x-1)-1}{2\cos x}=\boxed{{\displaystyle -\frac{1}{2}}}.\end{array}$$

$$\underset{x\to 1/2}{lim}\frac{1-2x+\ln (2x)}{1-4x+4x^2}=\underset{x\to 1/2}{lim}\frac{-2+(1/x)}{-4+8x}=\underset{x\to 1/2}{lim}\frac{-2x+1)}{8x^2-4x};$$

questo è di nuovo una forma indeterminata, che si può risolvere semplificando la quoziento oppure applicando di nuovo la regola de l'Hôpital per ottenere $\boxed{{\displaystyle -1/4}}$.

$$\underset{x\to 0^{+}}{lim}\frac{e^x-1}{x^2}=\underset{x\to 0^{+}}{lim}\frac{e^x}{2x}=\boxed{{\displaystyle \mathrm{\infty }}}.$$