Gauss, nello studio delle superfici curve, pubblicato a Gottinga nell'ottore del 1827, introduce un concetto fondamentale: il concetto di curvatura oggi detta gaussiana. Per una superfice sferica di raggio R la curvatura K viene definita come l'inverso del raggio al quadrato: K =1/R² di modo che, più è grande il raggio della sfera più è piccola la sua curvatura. Questa curvatura è la stessa in ogni punto della sfera e in questo caso è facile capire cosa si debba intendere per quantità di curvatura contenuta in una certa area della sfera: sarà i prodotto di questa area per 1/R² di modo che la curvatura totale di tutta la sfera sarà 4.
In generale Gauss definisce per qualunque punto P di ogni superficie S abbastanza regolare (ad esempio dotata in ogni punto di una sfera osculatrice, una sfera cioè che meglio di ogni altra approssima la superficie in quel punto) un numero positivo o negativo K_P detto la curvatura della superficie in P che, nel caso S sia una sfera restituisce il concetto standard di curvatura. Inoltre Gauss, seguendo l'esempio della geometria sferica di Menelao, dati due punti A e B sulla superficie S considera tutti i cammini che collegano A con B attraverso delle curve tracciate sulla superficie e chiama geodetico il cammino pił breve. Dimostra che dati A e B (abbastanza vicini) esiste sempre una geodetica che li collega e, come nel piano e sulla sfera, considera questa linea geodetica come il "segmento" che collega A con B. Dati inoltre due "segmenti" AB e AC si può considerare l'angolo tra questi due segmenti come l'angolo tra i vettori tangenti in A alla curva AB e alla curva AC. Possiamo in questo modo parlare di triangoli geoedetici e sviluppare una geometria intrinseca sulla superficie S che comprende come caso particolare la geometria piana, dove le geodetiche sono segmenti, e la geometria sferica dove le geodetiche sono archi di cerchi massimi. Nei due casi la curvatura è costante, zero nel piano, 1/R² nella sfera. La superfici che considera Gauss diventano degli spazi geometrici bidimensionali curvi dotati di "distanza" , "triangoli", "angoli", "cerchi" , "poligoni" ecc esattamente come nella geometria ordinaria.
Uno dei teoremi più importanti che Gauss dimostra e che sarà variamente generalizzato, riguarda la curvatura totale contenuta in un triangolo geodetico T della superficie S di angoli , , :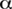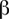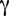

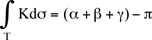
Per una superficie S compatta, per la quale quindi si possa calcolare la curvatura totale, la quale dipende solo dalla forma della superficie S, possiamo generalizzare l'argomento usato per la sfera, relativo alla sua caratteristica di Eulero-Poincar&eacue;. Ricopriamo la superficie S con una rete finita di triangoli geodetici e sia F il numero di triangoli, S quello degli spigoli della rete e V quello dei vertici, consideriamo la somma alternata 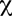= F - S + V detta caratteristica di Eulero-Poincaré della triangolazione. Abbiamo sommando la curvatura su tutti i triangoli

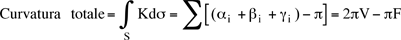
e quindi, dato che ogni triangolo ha 3 spigoli ma ogni spigolo è comune a due triangoli, abbiamo, come nel caso della sfera, 3F=2S e quindi

2V - F = 2V - 3F + 2F = 2V - 2S + 2F = 2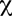 In definitiva

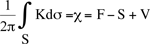
Ne segue che la caratteristica di Eulero-Poincaré non dipende dal tipo di triangolazione eseguita (cioè dal numero di triangoli coi quali abbiamo ricoperto la superficie) ma sola dalla sua forma globale, dalla sua curvatura totale. Viceversa, dato che la curvatura totale della superficie dipende dalla caratteristica di Eulero-Poincaré e dato che questa caratteristica non cambia se modifichiamo con continuità la superficie essendo un invariate topologico, abbiamo che la curvatura totale ad esempio di una sfera o di un uovo o di una qualunque altra superficie omeomorfa alla sfera è sempre la stessa.