non è uguale per tutti i triangoli ma dipende dalla sua grandezza: più il triangolo è piccolo (rispetto al raggio della sfera) e più questo eccesso diminisce e il triangolo assomiglia a un triangolo piano in accordo con l'intuizione che ci fa immaginare come piatta una piccola zona di una grande sfera.

Vediamo esattamente quale relazione intercede tra questo eccesso e l'area del triangolo sferico. Cominciamo col considerare uno spicchio della superficie sferica di ampiezza : lo spicchio è delimitato dai due semicerchi AMA' e ANA' e questi semicerchi sono ottenuti intersecando la sfera con i piani AMO e ANO i quali formano un angolo che quindi, per come è stato definito l'angolo tra due archi di cerchio massimo su una sfera, sarà anche l'angolo tra i due archi MA e NA. I due punti A e A' essendo estremi di un diametro della sfera sono antipodali.

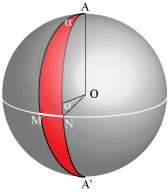Se R è il raggio della sfera, l'area A dello spicchio sarà proporzionale ad e quindi essendo 4R² l'area di tutta la superficie sferica, abbiamo la proporzione

4R² : A = 2 :

da cui

A = 2R²

Consideriamo ora un triangolo sferico A,B,C e sia T la sua area. Per ogni angolo consideriamo il doppio spicchio definito da quell'angolo come nella figura seguente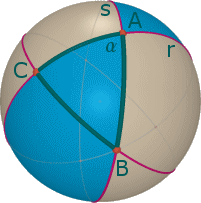

Questo doppio spicchio contiene il triangolo ABC e anche il triangolo antipodale A'B'C' dato che il punto antipodale di C si trova sull'arco AC e il punto antipodale di B si trova sull'arco BA. L'area di questo doppio spicchio vale 4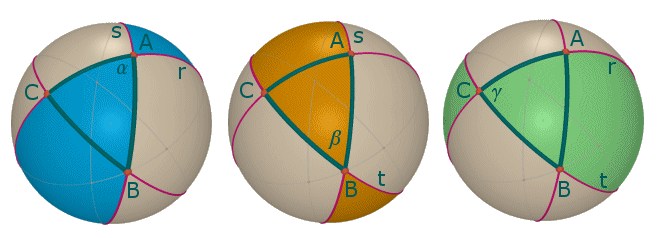R².
Ripetendo questo ragionamento per gli altri due doppi spicchi

osserviamo che la loro unione ricopre tutta la superficie sferica però il triangolo ABC e A'B'C' sono contenuti in ognuno dei tre spicchi e sono quindi contati 6 volte invece di due. Abbiamo quindi

4R² = 4R² + 4R² + 4R² - 4T

e quindi l'area T del triangolo sferico vale

T = R²[( + + ) - ]

Consideriamo ora un poliedro convesso P a facce triangolari e sia F il numero delle sue facce, V il numero dei suoi vertici e S il numero di suoi spigoli. Il teorema di Eulero stabilisce una sorprendente relazione tra questi numeri che non dipende dal tipo di poliedro considerato. Si consideri quindi una superficie sferica S di raggio R contenente il poliedro e dal centro della sfera si proiettino gli spigoli di P. Ad ognuno degli spigoli di P corrisponderà un arco di cerchio massimo e a ognuna delle facce di P corrisponderà un triangolo sferico i cui vertici sono i corrispondenti dei vertici del poliedro P. L'area di ogni triangolo sferico è data, come abbiamo visto, dal prodotto della differenza tra la somma dei suoi angoli interni e l'angolo piatto per il quadrato del raggio. L'area della superficie sferica è uguale alla somma di tutte queste aree, cioè alla somma di tutti gli angoli dei triangoli meno tanti angoli piatti quante sono le facce. La somma di tutti gli angoli interni è tanti angoli giro quanti sono i vertici. Quindi

(2 V - F) R² =4 R²

D'altro lato il numero dei lati S è uguale alla metà del triplo del numero della facce, perché ogni lato è comune a due triangoli contigui:

sostituendo nell'espressione V-S+F, V con (F+4)/2 ed S con (3F)/2 troviamo la sorprendente relazione

Se P ha facce poligonali (quindi non necessariamente triangolari) la sua proiezione sulla sfera sarebbe un reticolato di poligoni sferici che, nel caso avessero più di tre lati, potrebbero essere suddivisi in triangoli tracciando le loro diagonali. Per ogni diagonale tracciata, si ha un incremento di una unità sia nel numero dei lati che nel numero delle facce e la relazione tra i numeri di facce, spigoli e vertici rimane immutata. Dunque in generale si ha che in ogni poliedro convesso il numero delle facce più il numero dei vertici supera di due unità il numero di spigoli.