Coni circolari e loro sezioni

3. Strumenti reali e strumenti virtuali per tracciare le coniche

Indichiamo ora un metodo del tutto elementare per risolvere in modo geometrico l'equazione della conica y² = px + qx², per trovare cioè la y data la x. Il metodo, di origine pitagorica, può essere utile per realizzare con dei software di geometria dinamica come Cabrì o Cinderella il disegno di una conica come luogo e visualizzare la sua forma a seconda dei valori dei parametri p e q. Il problema consiste nel trovare il lato y di un quadrato la cui area sia uguale a quella di un rettangolo di lati x e p+qx. Per ragioni di dimensioni il parametro p sarà rappresentato da un segmento, mentre il parametro q da un rapporto (una pendenza m:n) in modo qx possa essere rappresentato da un segmento, il quarto proporzionale nella proporzione m:n = x:qx. In questo modo l'equazione è traducibile in termini geometrici e la soluzione è facilmente costruibile. Nella figura animata che abbiamo realizzato, possiamo cambiare la grandezza del segmento p e modificare la pendenza q.

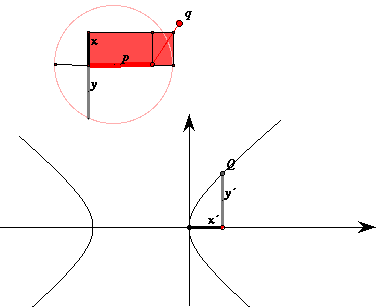
Fissato un segmento x iniziale su una retta orizzontale (l'asse delle ascisse) si costruisce il rettangolo rosso che è diviso in due parti: la prima di lati x e p e la seconda di lati x e qx. Questa seconda parte viene aggiunta nel caso dell'iperbole (nperbolh che significa eccesso, andare oltre) o tolta nel caso dell'ellisse (elleiyis che vuol dire mancanza, difetto, togliere) o ignorata nel caso della parabola (parabolh che vuol dire applicazione senza togliere o aggiungere nulla). Il segmento che rappresenta il lato del quadrato di area y² è costruito con la circonferenza rosa come quarto proporzionale tra x e p+qx. Questo segmento è poi riportato come ordinata sulla x. Il luogo è ovviamente descritto dal movimento di x lungo l'asse delle ascisse. Cambiando col mouse la pendenza q (q > 0, q = 0, q < 0) si passa da un tipo di conica a un'altra.

I termini con cui Apollonio chiama le coniche e che si usano nello stesso significato ancora oggi, sono diverse da quelli usati dai suoi predecessori (Archimede e Menecmo) e, secondo alcuni storici, essi derivano dagli antichi studi dei pitagorici sulla così detta applicazione delle aree. Si tratta, nel caso più semplice, dato un segmento a e un'area quadrata y², di "applicare" a quel segmento un altro segmento x in modo da formare un rettangolo di lati a e x e di area uguale a quella data (in termini numerici ax = y² applicazione parabolica), oppure si applica su a un segmento x in modo da formare un rettangolo di area uguale a quella data la cui base però è una parte di a e la parte mancante genera un quadrato (in termini numerici y²=ax-x² applicazione ellittica) o ancora si applica su a un segmento x in modo da formare un rettangolo di area uguale a quella data la cui base però eccede a di un quadrato (y²=ax+x² applicazione iperbolica). La soluzione geometrica di questi problemi che si basa sul teorema dello gnomone, forma il corpo principale delle tecniche di algebra geometrica nella matematica antica. Esse si riducono oggi alle formule risolutive per le equazioni di secondo grado.

I metodi scoperti da Apollonio permettono di disegnare facilmente, per punti e in modo esatto tutte le possibili coniche. Non sappiamo se tali metodi fossero noti nel rinascimento. Alberti e Piero della Francesca riconoscono chiaramente che lo scorcio di un cerchio è una sezione piana di un cono ma suggeriscono metodi empirici per disegnarlo. Leonardo inventa e probabilmente costruisce dei compassi in grado di tracciare esattamente le coniche. L'idea di Leonardo è molto semplice ma nello stesso tempo richiede un "ricentramento cognitivo". Normalmente pensiamo il compasso come uno strumento che con la sua rotazione genera un cono la cui sezione sul piano del foglio sempre orizzontale è una circonferenza. Il cono che immaginiamo ha la base circolare orizzontale e l'asse verticale. Se si vogliono ottenere da quel cono delle sezioni che non siano circolari diventa necessario intersecarlo con un piano obliquo cosa quanto mai complicata se si vuole disegnare il risultato di tale intersezione. L'idea di Leonardo è quella di inclinare l'asse intorno a cui ruota il compasso mantenendo invece orizzontale il foglio da disegno. In questo modo la gamba del compasso che contiene la mina, man mano che ruota appoggiandosi al foglio, mantenendo lo stesso angolo con l'asse fisso, cambia lunghezza. Basterà quindi inventare un meccanismo che permetta di adattare la lunghezza della gamba alle necessità. Una possibilità è ad esempio quella di far scorrere la gamba mobile in un binario facendola aderire al foglio sotto la pressione di un peso o della mano che la spinga in basso. Nel seguente compasso realizzato sulla base di progetti leonardeschi

l'asse è tenuto ben fermo dal treppiedi mentre la matita, che scorre in un suo binario, viene fatta scendere a mano. In quest'altro compasso realizzato pare per costruire specchi parabolici, il piano del foglio è opportunamente inclinato in modo da renderlo parallelo alla generatrice.

L'apertura del cono è di 45 gradi in modo da rendere più agevole fissare l'angolo (con una semplice squadretta) che non deve cambiare durante la rotazione attorno all'asse. Un peso, ben visibile spinge la matita verso il foglio.
Il contenuto matematico di questi strumenti è evidente: essi disegnano la curva che si ottiene intersecando un cono retto con un piano, dunque una conica.

Problema Le coniche si possono realizzare tutte su un cono retto e aperto a 90 gradi?