Euclide

Ottica

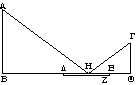
Sia AB un'altezza, sia G l'occhio e sia necessario sapere quanto è grande AB quando non c'è sole. Si ponga in terra lo specchio DZ e sia prolungato il [segmento] DB allineato con ED, finché si incontra con l'estremo B della grandezza AB; incida il raggio GH dall'occhio G e venga riflesso finché si incontra con l'estremo A della grandezza AB; sia prolungato EQ da DE, e sia tracciato da G il [segmento] GQ perpendicolare ad EQ.

Poiché dunque incide il raggio GH e viene riflesso HA, e sono riflessi secondo angoli uguali, come è detto nella Catottrica, allora l'angolo in GHQ è uguale a quello in AHB. Ed anche quello in ABH è uguale a quello in GQH; quindi anche il restante [angolo] in HGQ è uguale al restante [angolo] in HAB . Quindi il triangolo AHB e il triangolo GHQ sono equiangoli. Ma i lati dei triangoli equiangoli sono proporzionali . Allora GQ sta a QH come AB sta a BH. Ma il rapporto tra GQ e QH è noto; allora anche il rapporto tra AB e BH è noto. Ma HB è noto. Quindi anche AB è noto.