Il paradosso dell'angolo di contingenza

di Franco Ghione

Prologo

Ho avuto occasione di leggere, prima della stampa definitiva, l'articolo di Laura Catastini Il sasso e la lanterrna che tratta, tra l'altro, di un concetto che avevo sempre creduto di poter dominare, come ogni geometra, in ogni suo aspetto: il concetto di angolo. Con mia grande sorpresa invece, la lettura e il filo dei ragionamenti mi ha coinvolto in una rete di paradossi, di dubbi, di stranezze storiche che mi hanno spinto a riaprire gli occhi su questa materia, soffiandone via la polvere per rientravi, in modo nuovo e leggero, con lo spirito di Alice. Alice ha voluto accogliere questi miei commenti pensando forse che altri, di altri lettori, se ne possano aggiungere.

Il paradosso dell'angolo di contingenza.

Il paradosso dell'angolo di contingenza come mi piacerebbe chiamarlo, ha suscitato nella storia del pensiero scientifico dispute accanite che hanno coinvolto, tra gli altri, personaggi come Proclo, Clavio, Cardano, Galileo, Newton, Leibnitz e le cui tracce, come l'articolo di Catastini mette chiaramente in luce, sono ancora presenti in confuse immagini mentali sulla nozione di angolo che riecheggiano drammaticamente nei manuali scolastici e nei pregiudizi dei nostri studenti universitari. Ragionare sui paradossi, che la considerazione dell'angolo di contingenza o più in generale dell'angolo curvilineo suscita, consente di mettere a nudo le immagini mentali scorrette che non permettono al pensiero di dominare e capire un concetto tanto elementare quanto di base come quello di angolo.

Enriques nella sua versione degli Elementi di Euclide, dove troviamo un'ampia e documentata analisi storica delle dispute alle quali accennavo più sopra, (Gli elementi di Euclide e la critica antica e moderna) nell'enunciato della proposizione III, 16 omette una parte che invece troviamo nell'edizione, più letterale, curata da Frajese e riportata nell'articolo di Catastini: "... e l'angolo del semicerchio è maggiore, e quello che rimane [fra la retta e la circonferenza] minore, di ogni angolo acuto rettilineo" Questa chiosa, forse spuria, è all'origine della disputa. Essa presuppone che si possano confrontare angoli rettilinei e angoli curvilinei, ma, se questo confronto è possibile (e andrebbe chiaramente detto come poterlo fare) e se l'angolo di contingenza è una grandezza minore di ogni altra grandezza angolare, allora questa grandezza dovrebbe essere necessariamente nulla. D'altra parte se l'angolo di contingenza è nullo come mai esiste una parte di piano ben chiara e sicuramente non nulla compresa tra le due linee, l'arco di circonferenza e la sua tangente?
Insomma l'angolo di contingenza è nullo o non è nullo? Come può una grandezza nulla contenere qualcosa?
Il riferirsi all'immagine (scorretta come Catastini dimostra) dell'angolo come estensione, come parte di piano, induce inevitabilmente l'idea che l'angolo di contingenza non possa essere nullo pur essendo minore, come afferma la III 16 di Euclide, di ogni altro angolo rettilineo. E' forse allora un oggetto "infinitesimo"? Ma in questo caso gli angoli non sarebbero più grandezze archimedee perché nessun multiplo di un angolo di contingenza può superare un angolo rettilineo anche piccolissimo. Ma se non sono grandezze archimedee di che tipo di mostruose grandezze si tratta? E come possiamo rapportarle tra loro? Da questo non si esce: o l'angolo di contingenza è nullo o gli angoli rettilinei e curvilinei non sono grandezze archimedee.

D'altra parte in geometria differenziale la nozione di angolo tra due linee differenziabili uscenti da uno stesso punto su una qualunque varietà differenziabile di dimensione qualunque è ben chiara: le due linee definiscono nel loro punto di contatto due direzioni tangenti e l'angolo tra le due linee non è altro che l'inclinazione di una direzione sull'altra, grandezza che è possibile misurare attraverso la prima forma fondamentale che fornisce alla varietà differenziabile la sua struttura metrica. Si vede dunque che, nel caso dell'angolo di contingenza, poiché le due direzioni coincidono, non c'è inclinazione di una sull'altra e per questo l'angolo risulta necessariamente nullo. Nessun paradosso dunque, nessun comportamento non archimedeo nessuna meraviglia: ogni multiplo di zero è sempre zero come si deve! Angoli rettilinei e curvilinei possono essere considerati insieme possono essere confrontati tra loro e misurati.

Resta tuttavia, per l'angolo di contingenza, una curiosa incongruenza di carattere soprattutto percettivo che ancora ha a che fare con l'incantesimo che ci porta a immaginare l'angolo come estensione. Il fatto è che ci sono diversi angoli di contingenza, diversi "zeri" confrontabili tra loro, o anche, come già osservava Campano nel XIII secolo, divisibili in due parti ch e potremmo pensare uguali. L'immagine seguente mostra un angolo di contingenza "diviso in due parti uguali" in (a), in tre "parti uguali" in (b) e in quattro "parti uguali" in (c).

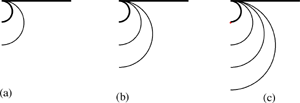
Il fatto di avere diviso in parti uguali l'angolo di contingenza può essere in questo caso perfettamente definibile senza riferirsi alla divisione in parti uguali di una regione di piano (che sarebbe eventualmente illimitata e pertanto non facilmente divisibile), ma riferendosi al raggio del cerchio: potremmo dire coerentemente che la "bisettrice" dell'angolo di contingenza si ottiene raddoppiando il raggio del cerchio tangente, un terzo dell'angolo di contingenza si ottiene triplicando il raggio, un quarto quadruplicando ecc. Notiamo come, da un punto di vista percettivo, le "aree" che si ottengono dividendo "in parti uguali" secondo questa definizione, non appaiono alla vista uguali rendendo fuorviante questo tipo di riferimento all'intuizione.

Sembra quindi che nel confrontare angoli rettilinei con angoli di contingenza questi debbano essere considerati nulli, mentre confrontandoli tra loro sia possibile definire una qualche naturale gradazione interna. Newton liberandosi definitivamnte dall'incantesimo riuscì, come diremmo oggi con un drestico ricentramento cognitivo, a vedere nel "angolo" di contingenza tutt'altra cosa: la curvatura. Riuscì a vedere una "qualità" diversa come aveva intuito Proclo da considerarsi a se e da interpretare geometricamente in tutt'altro modo.
L'articolo di Catastini mettendo in luce le conseguenze negative che nascono da una cattiva gestione didattica del rapporto tra intuizione ed immagini mentali spiega la fatica (quasi sempre insormontabile) che debbono fare gli studenti nei corsi universitari per collegare gli oggetti che vengono via via introdotti con la loro immaginazione ed esperienza reale. Si finisce inevitabilmente per darsi per vinti rifugiandosi nei soli contenuti formali e rinunciando a sviluppare quel rapporto tra intuizione e formalismo che trova nella Matematica a tutti i livelli, la sua più piena realizzazione.

Epilogo

In un punto di una curva differenziabile abbiamo sempre una retta tangente (associata alla derivata prima) e un cerchio osculatore (associato alla derivata seconda). Retta e cerchio formano sempre un "angolo di contingenza" che è più o meno grande a seconda che il raggio del cerchio sia più o meno piccolo cioè a seconda che la curvatura in quel punto sia più o meno grande.
Il nodo si è sciolto e sciogliendosi ha dato origine a due nozioni geometriche completamente diverse: la nozione di angolo (rettilineo o curvilineo che sia) e la nozione di curvatura, entrambe suscettibili di misura, entrambe archimedee. Ora però, che si sono così nettamente separate, si possono rappresentare con due immagini completamente diverse tra loro e coerenti. L'angolo recupera il suo significato originale di inclinazione, di relazione tra due oggetti (le due semirette) mentre la curvatura ci racconta con quanta energia una linea differenziabile, nel suo tracciarsi, si discosti dalla direzione tangente piegandosi in un senso o nell'altro, passando dal concavo al convesso, tentennante nei punti di flesso

In questa linea inventata da Kandisky (Punto, linea superficie). abbiamo aggiunto in un punto la tangente e il cerchio osculatore (ottenuto come limite del cerchio passante per tre punti della curva quando i tre punti vanno a sovrapporsi) per mostrare come la misura della curvatura in quel punto (l'inverso del raggio del cerchio osculatore) sia "visibile "in termini di angolo di contingenza più o meno "grande".