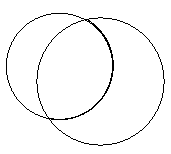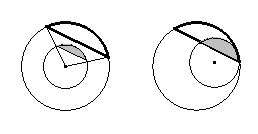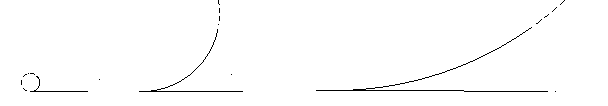|
Compiti divini
Il percorso e l'uso delle idee matematiche nel tempo spesso cambiano la forma nella quale tali idee vengono espresse, adeguandole a nuovi ambienti
e nuovi formalismi scientifici e rendendo così più agevoli le loro applicazioni, ma cancellano spesso ogni memoria e ogni fisionomia
delle problematiche dalle quali esse sono nate. La tradizione matematica ha tra i suoi non facili compiti quello di far diventare razionale ciò
che nasce intuitivamente. La comunicazione didattica invece spesso si trova davanti anche il problema inverso: restituire valore intuitivo a
definizioni razionali, astratte o conciliarle con ciò che in noi è già intuitivamente presente grazie alla normale frequentazione
delle cose della vita. A volte nella storia delle idee ritroviamo questo contatto stretto con la realtà e con l'intuizione proprio nel
momento in cui le abbandoniamo per seguire la costruzione del mondo rigoroso delle definizioni, dei teoremi, dei principi primi.
Riscoprire queste idee nella loro autentica dimensione analizzandone la genesi e le formulazioni originali non è solo occasione di
arricchimento culturale per tutti, docenti e discenti, ma permette a questi ultimi di costruire corrette rappresentazioni mentali degli
elementi e dei concetti fondamentali della materia che dovranno affrontare, correggendo modelli sbagliati formatisi spontaneamente nel tempo. La
rappresentazione è il risultato del modo con cui il pensiero si libera dagli stimoli immediati e riassume l'esperienza passata. Le immagini
mentali sono un utilissimo e spontaneo meccanismo di simulazione. Non sono solo forme di rappresentazione statica di aspetti di esperienze
vissute ma ne permettono aggiunte, esplorazioni e simulazioni dinamiche che possono spesso suggerire soluzioni a problemi da risolvere
1
.
La facoltà che mette in moto l'invenzione matematica non è il ragionamento ma l'immaginazione ha detto A. De Morgan. Nel
campo scientifico però è di fondamentale importanza che il rigore delle rappresentazioni mentali sia tale da renderle "modelli"
scientificamente corretti. Solo allora potranno produttivamente sostituire le naturali rappresentazioni "ingenue" derivanti dall'uso
non tecnico del linguaggio e dei concetti matematici nella vita di tutti i giorni o dal cattivo apprendimento scolastico dei concetti
stessi in fasi precedenti.
Siamo d'accordo con Enriques quando dice che
Importa - non solo - l'attitudine a vedere passivamente un modello che si metta sott'occhio allo
studioso, ma anzi la capacità di foggiare - come oggetto della fantasia - un modello possibile, cui si impongono, a priori, talune condizioni:
ed una tale attività costruttiva che ordina i dati di osservazioni ed esperienze passate, non è pura fantasia o fantasticheria,
sciogliente il freno al libero giuoco delle associazioni d'idee, bensì una vera attività logica.
2
L'attenzione didattica a questa attività costruttiva educa insieme l'intuizione e la logica, vedendole non come attività separate e
distinte dell'intelligenza, bensì come due aspetti inscindibili di uno stesso processo attivo nel quale si richiamano l'un l'altra.
Gli argomenti qui proposti non vogliono far parte di unità didattiche ma intendono creare piccole isole di riflessione tra le unità
programmate. Ogni tanto fa bene fermarsi e muovere il pensiero non per imparare supinamente qualcosa (tecniche o teorie) ma per discutere in
modo costruttivo su qualcosa. Questo è il senso dell'insegnamento dinamico che auspica Enriques, il quale ammette che il compito che
ci è proposto è tremendamente, stavo per dire divinamente, difficile ma anche ammonisce
Non c'indugiamo a cercar pretesti,
dando tutta la colpa all'infingardaggine degli studenti (che appunto si tratta di vincere) o all'obbligo di svolgere un dato programma, con
un orario troppo ristretto ecc. ecc.
Questo "divino" compito si muove sul terreno dei modelli ingenui presenti nella mente dell'alunno, prefiggendosi lo scopo di svolgere su di essi
un'azione educativa . Indizi dello stato iniziale delle rappresentazioni naturali degli studenti traspaiono spesso dalle loro domande. Durante
una lezione sulla forza di gravità una mia alunna se ne uscì in questo modo:
"Professoressa, ma si casca sempre in piedi?"
Indovinello:
quale situazione stava immaginando la ragazza? Perché ha avuto bisogno di chiedere questo strano chiarimento? Quale modello la stava guidando
nei ragionamenti?
Il sasso e la lanterna
Roberto Casati, autore del libro La scoperta dell'ombra, si occupa, per mestiere, della cognizione di oggetti strani.
Stava osservando un'eclisse totale di luna, racconta, quando lo scivolare del cono d'ombra sul corpo della luna produsse nella
sua mente uno scatto imprevisto, facendogli vedere nel cielo un oggetto diverso da quello di sempre:
Per la prima volta ho visto la luna per quello che è veramente [...] La luna è un sasso tenebroso piuttosto cospicuo
che se ne sta a una certa distanza sopra la mia testa e stranamente non mi cade addosso. Naturalmente conoscevo le leggi che la tengono
ben salda in orbita, ma i miei occhi, non abituati a vedere pietre sospese nel cielo, non volevano sentire ragioni. Come del resto era
sfuggita ai miei occhi l'idea, peraltro a me perfettamente nota, che la luna sia un grosso sasso scuro: di solito la luce diafana della
superficie lunare regala allo sguardo l'illusione di una lanterna delicata e leggera [...] La luce conferisce alla luna una leggerezza
che rende più accettabile, quasi normale, il suo galleggiare nella notte come una lampada sul soffitto nero del cielo.
3
Questo breve racconto rende bene il carattere misterioso e multiforme del fenomeno della cognizione, del farsi e disfarsi delle rappresentazioni
mentali in funzione non solo di conoscenze razionali ma anche della compulsiva propensione del nostro cervello, guidato dalla pratica della vita
quotidiana, a creare oggetti stabili e strutturati in una realtà intimamente inafferrabile. E così Casati, improvvisamente, vede la
luna per quel che è veramente. Veramente? La luna è veramente una congrega di atomi stabili con una vibrazione termica
molto modesta
sospesa nel cielo solare, oppure veramente un' enorme distesa butterata attorno a cui ruota un piccolo corpo azzurro e bianco che
la osserva da
lontano, oppure è veramente uno strano puntino che si muove in maniera bizzarra rispetto a Giove? O è veramente
qualcos'altro?
Dal punto di vista cognitivo niente veramente qualcosa, e tutto si articola in forme in funzione dello sfondo creato dagli
occhi della mente, diventando per un po' qualcosa, che svanisce quando il mutare del pensiero porta con sé il mutare dello sfondo.
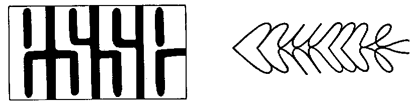
Qual è veramente il contenuto delle due figure, immagini o parole?
fig. 1
Nell'opera di Casati questo fatto viene continuamente mostrato attraverso la descrizione delle credenze e delle concezioni storiche che
stanno dietro il fenomeno dell'ombra, strano caso in cui l'assenza di qualcosa - la luce - diventa una presenza, la presenza di un
oggetto - l'ombra - con le caratteristiche fisiche proprie di tutti le presenze reali, generando confusioni ed errori nella predizione
del suo comportamento anche in persone con un alto grado di istruzione.
L'ombra di fatto viene percepita con una sua forma, un suo colore e come emanazione del corpo che la proietta. Nei bambini il primo smarrimento
avviene quando si rendono conto che l'ombra non si comporta come tutti gli altri oggetti: se coperta di sassolini non sparisce, non gira se
il corpo gira su se stesso, non si stende sul muro come un getto d'acqua, semplicemente puntandovi contro l'oggetto, non si può
trascinare spostandola con i piedi. Gli esperimenti degli psicologi mostrano che i bambini sanno che l'ombra non è un oggetto,
ma quando possono continuano a trattarla come tale, sbagliando la previsione del risultato delle proprie azioni su di essa. Anche il
modello adulto però non è esente da contraddizioni: se per esempio sostiamo sotto un albero a mezzogiorno, diciamo di essere
all'ombra, mentre se camminiamo di notte per la strada non ci sembra di esserlo, anche se siamo effettivamente nel cono d'ombra della terra. Non
riconosciamo infatti la presenza dell'ombra se non coesiste con zone di luce che permettano lo stagliarsi di contorni
e di figure tenebrose.
Anche noi adulti quindi sappiamo che l'ombra non è un oggetto, ma quando possiamo continuiamo a trattarla come tale. La costruzione razionale
di un modello ci aiuta nei casi semplici a padroneggiare il fenomeno dell'ombra, ma basta fare domande leggermente complesse per mostrarne
tutta la fragilità. In un esperimento veniva somministrato a studenti dei primi anni universitari un questionario su fatti astronomici
elementari. Le risposte riguardanti domande in cui entravano in gioco le ombre erano sorprendenti. Una buona percentuale degli studenti, ad
esempio, pensava che le fasi della luna fossero dovute all'ombra proiettata sulla luna dalla terra
4
. Il motivo di questa difficoltà a
muoversi tra le ombre è dovuto al modo in cui queste si definiscono implicitamente attraverso la percezione, l'esperienza, il linguaggio
con cui sono trattate, nell'assenza di definizioni complete e adeguate al costituirsi di un buon modello scientifico. Si consolida così
nella mente un concetto che mette insieme aspetti causali, materiali e percettivi: l'ombra è partorita dalla luce, ha una sua figura e
una sua materialità (sottile come un'ombra, l'ombra si allunga e si accorcia). La tendenza a vedere l'ombra come una cosa spesso è
più forte della concezione razionale che ne abbiamo e ci mette in uno stato di leggera confusione di fronte a problemi come questo:
"A mezzogiorno teniamo un mattone sospeso su un tavolo e osserviamo la sua ombra. Dal momento che è mezzogiorno, l'ombra sarà
uguale al mattone, posta perpendicolarmente sotto di lui. Appoggiamo ora il mattone sul tavolo. La sua ombra c'è ancora?"
Il senso comune quindi oscilla tra il trattare le ombre come oggetti concreti con proprietà familiari, e il considerarle invece come
enti incorporei non ben definiti, come cose strane, non appena la rappresentazione "materiale" si mostra in tutte le sue contraddizioni e
perciò inadeguata.
Cose
L'attribuzione di oggettualità all'"oggetto"
5
dipende da fattori che includono il nostro stato interiore nella situazione immediata; per esempio alcuni tratti del segnale visivo che
interagiscono con l'intenzione o il bisogno del momento possono rendere alcuni "oggetti" più salienti di quanto essi non avrebbero
potuto essere in altri casi o possono individuarne di nuovi: due tavolini di diversa altezza accostati tra loro possono per esempio essere
visti come una scala per chi deve urgentemente raggiungere un oggetto posto in alto.
Allo stesso modo possono contribuire a creare o meno degli "oggetti" anche quei tratti del segnale visivo che interagiscono con la conoscenza
dell'osservatore; per esempio un esperto elettricista vedrà immediatamente il disegno di un complesso circuito elettrico aggregarsi
in sottoschemi significativi e in "oggetti" ben classificabili, là dove un neofita vedrebbe solo un intricato insieme di linee. Questo
accade anche per altri canali percettivi: i suoni di una catena acustica prodotta ad esempio da un cinese si spezzano per un suo connazionale,
in una sequenza di unità uditive (le parole) mentre per chi non conosce la lingua la stessa catena acustica è percepita come un
flusso indifferenziato di suoni.
Le cose, strane o normali che siano, entrano con prepotenza nella nostra percezione e del nostro pensare. Descriverle è in realtà
crearle:
Limitarsi a descrivere è così difficile perché si crede che per comprendere i fatti sia necessario integrarli. È come se
uno vedesse uno schermo su cui sono sparse macchie di colore e dicesse: così come sono, sono inintelligibili; acquisteranno senso solo se
le si integra in una figura. - Mentre quello che io voglio dire è, invece: è tutto qui. (Se lo integri lo snaturi)
6.
Non si può dire "è questo" di qualcosa, come Wittgenstein scopre con stanco stupore di filosofo, senza decidere come strutturare
ciò che vediamo.
Allora è così: "Io ho sempre letto il segno S come un sigma; ora qualcuno mi dice che
potrebbe anche essere una M ribaltata, e adesso sono in grado di vederlo anche così - perciò prima l'ho sempre visto
come sigma"?
Questo vorrebbe dire, insomma, che la figura S io non l'ho soltanto vista così, ma l'ho anche
vista come la tal cosa!
7
Come nel caso dell'ombra, creiamo continuamente "cose". Prendiamo ad esempio i buchi: non ci sono, non esistono i buchi, esistono cose bucate,
la cui forma è impegnativa da descrivere.
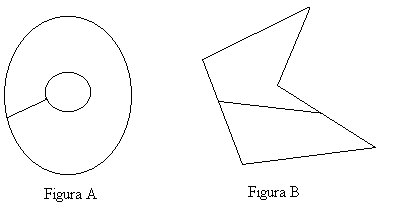
fig. 2
Potremmo dire che le cose sono bucate quando è possibile trovare due punti del loro contorno tali che se ci diamo un taglio
attraversando la figura non dividiamo la cosa in due pezzi (figura A), mentre nelle cose senza buchi questa operazione non è
possibile (figura B).
Questo modo di vedere la cosa bucata è sicuramente più vicino a un punto di vista scientifico, ma innaturale e antieconomico
per il nostro sistema percettivo.
Se volete che qualcuno ritagli in un foglio di carta un buco a forma di stella, la cosa più semplice è proprio di chiedergli
di ritagliare un buco a forma di stella.
8
La stella è la descrizione della forma del buco, che va sostituire quella del bordo interno
del foglio di carta - molto laboriosa da descrivere a chi dovesse ritagliarla, provare per credere - che è la sola legittima cosa materiale
che abbiamo. Sostituiamo così alla forma informe
9
del concreto ed esistente margine interno del foglio, quella stellare di una cosa che non
c'è. Le implacabili leggi gestaltiche della "buona forma" la fanno in questo caso da padrone, imponendo alla nostra mente esistenze
discutibili. Riusciamo perfino a vedere buchi nell'ombra. Pensate all'ombra di una grata. Riusciamo a rendere supporto materiale di una cosa
che non c'è - il buco - una cosa che non c'è - l'ombra!
Questa singolare proprietà del nostro pensiero è necessaria per rendere stabile e rassicurante il nostro ambiente. Vedere un tappo
come tappo piuttosto che come zeppa da usare per fissare a incastro qualcosa ci mette in grado di infilarlo senza tanto pensare nel collo di
una bottiglia e vedere immediatamente due persone disegnate sul foglio invece di stare un'ora a tentare di decifrare i loro spazi
complementari (fig. 3), è espressione della nostra capacità di adattamento all'ambiente.
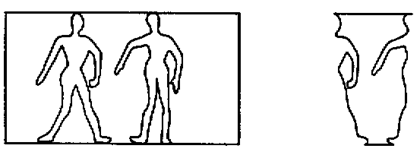
fig. 3
L'atto del vedere non riesce spesso liberarsi dall'alone di concretezza che le figure emanano. Il fatto è che il nostro sistema biologico
è costruito per vivere piuttosto concretamente, occupandosi di cose prosaiche come procacciarsi il cibo, riprodursi, difendersi dalle
aggressioni, e tutto questo in stato di continuo movimento, nostro e delle cose che ci stanno intorno. Il sistema visivo mantiene il più
possibile stabile la riproduzione dei nostri quadri di percezione attraverso complicati meccanismi fisiologici e formandosi quadri di
riferimento che stiano fermi mentre gli occhi si muovono. I sistemi di riferimento sono un fattore importante nella formazione delle figure
Il più semplice è quello formato dai nostri occhi. Quando saltelliamo, per esempio, non vediamo un mondo sobbalzante, ma
relativamente stabile. Un altro quadro di riferimento fondamentale è la direzione della gravità. L'asse mentale alto-basso
è un potente organizzatore delle nostre forme:
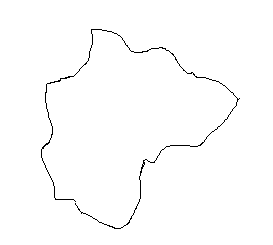
fig. 4
Di solito in questa figura non viene vista l'Africa ruotata di novanta gradi
10
. È un'altra cosa
11
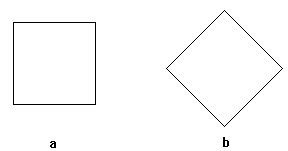
fig. 5
Anche in questi due disegni si vedono due cose diverse, ma l'unica differenza tra di loro sta nel fatto che sono disposti in modo diverso rispetto
al sistema di riferimento alto-basso: il quadrato presenta in alto un lato nella situazione (a), e un vertice nella situazione (b) e questo
gli basta per ritrovarsi due nomi diversi. Come dice lo psicologo Pinker
12
"all' "in alto" non si sfugge "
13
!
A proposito di "in alto", è ora il momento di ricordare la domanda della mia alunna: "Ma si casca sempre in piedi?". Alla richiesta
di riformulare la domanda in altri termini, lei precisò: "Se la terra fosse sopra la nostra testa, noi ci cadremmo sopra ugualmente? ne
saremmo sempre attratti? ". In altre parole stava chiedendo: "come si può cadere in basso se abbiamo la terra in alto?" rendendo evidente
che faceva della sua testa "l'alto", dei suoi piedi "il basso" e del suo corpo l'asse di riferimento verticale dell'intero universo in maniera
così totale da non riuscire a spostarne l'origine nel centro della sfera terrestre e a relativizzare così le situazioni che andava
simulando col pensiero
14
.
Quando gli impulsi della percezione visiva diventano "forme" e "oggetti", immaginate o effettivamente viste che siano, queste si caricano
automaticamente di un alone pragmatico che fa spesso "muovere" spontaneamente in una certa direzione il quadro percepito, nel senso che suggerisce
inferenze istintive e non intenzionali. Avete fatto caso per esempio, che in geometria esistono "cose sdraiate" e "cose in piedi"? Wertheimer
15
ci racconta la reazione, in una classe elementare, di parte dei bambini a cui era stato insegnato a dimostrare nel caso (a) che l'area del
parallelogramma è equivalente a quella del rettangolo di uguale base e uguale altezza, nel momento in cui si chiedeva loro di ripetere
la dimostrazione nel caso (b):
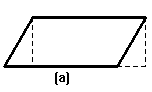 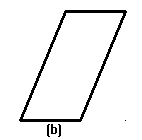
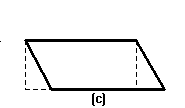
fig. 6
Prima protestavano dicendo che non l'avevano ancora studiato, poi, anziché procedere con le linee ausiliarie come imparato, preferivano
ruotare il foglio - caso (c) - e disegnarle nella situazione che ricreava "la solita cosa", cioè il parallelogramma "sdraiato". Non c'è
lettore, immagino, a cui risulti oscuro il motivo della difficoltà di questi bambini, che si stupisca del loro comportamento. E noi tutti
riusciamo a cogliere il cuore del problema perché "la figura è un'altra figura anche per chi sa che è la stessa "
16
.
Il nostro sistema nervoso è estremamente sensibile all'orientamento. L'inclinazione di una linea è riconosciuta immediatamente dalle
nostre cellule nervose, che rispondono ad essa in maniera selettiva
17
. Cellule per esempio che rispondono a 20 gradi di inclinazione hanno in questo
caso un massimo di scarica mentre rimangono silenti se l'orientamento se ne discosta. Un bambino di meno di sei settimane sa già
distinguere l'orientamento.
Gli assi di simmetria di una figura intervengono perciò ad aggiungere alle figure dinamicità e corpo. L'asse di simmetria non forma
un riferimento alto-basso, ma indica una direzione, quella dell'asse, e un verso destra-sinistra lungo la direzione stessa:

fig. 7
Il triangolo (b) è stabile, anzi "stabilissimo" con i suoi tre assi di simmetria, fermo ad accogliere, nella sua perfezione l'occhio di Dio,
mentre i triangoli (a) e (b) si presentano immediatamente puntati in direzioni contrastanti
18
, aprendo il quadro a dinamiche che gli artisti
conoscono bene e sono sempre pronti ad usare.
Infine quadri di riferimento possono essere formati da una congrega di oggetti:
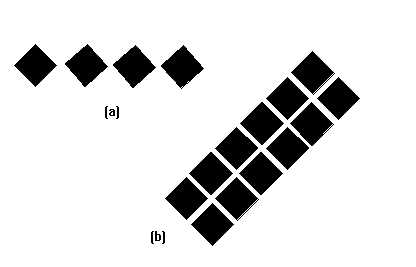
fig. 8
Le forme contenute in (b) appaiono come quadrati mentre in (a) appaiono come rombi. Questo perché il loro allineamento diagonale,
nel caso (b) crea un destino comune di corpi ugualmente inclinati sulla linea di terra. Se "appoggiati correttamente" a terra, questi
corpi sarebbero quadrati.
Un alone pragmatico quindi accompagna le figure geometriche più pure e gli oggetti euclidei hanno la capacità di attirare a
sé quadri di riferimento e caratteristiche bassamente terrene.
L'angolo: una cosa strana
Nella vita di tutti i giorni ci si incontra all'angolo della strada, si gira intorno all'angolo del caseggiato, si batte la testa proprio
sull'angolo del tavolo, si sollevano gli angoli della bocca, si sceglie un angolo da cui guardare, si tormenta il compagno di banco con
l'angolo della squadra. Questo avevano in mente gli alunni di un Istituto d'Arte quando ho chiesto se si ricordavano la definizione
(geometrica, s'intende) di angolo, e le prime vivaci risposte sono state del tipo "è l'intersezione tra due segmenti... no, è
il punto di intersezione tra due segmenti...no... è il punto di intersezione tra due semirette...", nello sforzo di
caratterizzare "la cosa" (che tale fosse non esisteva dubbio alcuno!) mediante il suo essere a punta, e di risolversi quindi in un punto. Fino
a quando l'alunno bravo, quello che aveva fatto il biennio al Classico e aveva poi chiesto il passaggio di Istituto approdando in mezzo a noi,
ha drammaticamente dato la definizione esatta: "l'angolo è la porzione di piano compresa tra due semirette uscenti da un
medesimo punto". In effetti questa definizione è quella che ormai si trova in tutti i testi di geometria elementare, e credo abbia
una grossa responsabilità nel rendere l'angolo una cosa confusa.
Vediamo innanzitutto cosa hanno contestato gli studenti: gli angoli del triangolo ABC dovrebbero essere uguali tra loro, perché
comprendono la stessa parte di piano, anche se si vede bene che sono diversi.
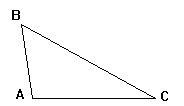
fig. 9
E poi, che dimensione ha l'angolo? Come parte di piano dovrebbe essere una cosa a due dimensioni. Ora, gli oggetti geometrici a due dimensioni
hanno dei "buoni" comportamenti a cui si attengono disciplinatamente. Per esempio, hanno un'estensione che si può misurare, si possono
sommare o sottrarre, possono essere equivalenti. Ha senso dire che due angoli sono equivalenti?
In classe si ricorda presto che la misura dell'angolo non è omogenea a quella delle altre figure a due dimensioni, che l'angolo non si misura
in metri quadri come ogni parte di piano che si rispetti, e di solito, allora, irrompe improvviso il grado come grande solutore della questione. Ma
dura poco. Il grado mal si concilia con la superficie perché è assimilato dagli studenti a una qualche forma di misura lineare,
associazione indotta dall'uso del goniometro. Inoltre si sentono complici (o vittime) di un sottile imbroglio perché, protestano, se lo
misurassero "più in là" l'angolo sarebbe più grande.
"È una specie di righello, ma curvo" è la seconda risposta degli studenti alla domanda "cos'è un goniometro?". La prima
risposta, nella migliore tradizione infantile è "Il goniometro è per disegnare gli angoli" Cioè, nella pratica, per
disegnare punte, più o meno aguzze. Il goniometro serve a disegnare linee spezzate ben determinate nella loro relazione. Queste non
sono viste come linee perimetrali di una superficie ma, giustamente, come rappresentazione di una "spezzatura "
19
. Il bambino di appena due mesi
che già riconosce l'orientamento, reagisce a questo stimolo
20
:

fig. 10
nello stesso modo in cui vi reagiamo noi, individuandovi non una porzione di piano ma un cambiamento di direzione.
Parte di piano o spezzatura? Non si riesce ad uscire, come per l'ombra, da un concetto ibrido che mette insieme in modo non scientifico aspetti
formali, materiali e percettivi, generando una cosa strana e confusa.
La confusione e il mistero, che a questo punto hanno già spento il sorriso e la vivacità dello studente sono spesso rinforzati
da moderni manuali scolastici per bienni unici. Mi è capitato di leggere su un "modulo" per biennio di Logica e geometria euclidea del piano,
subito dopo l'elenco dei concetti primitivi tra cui era stata inserita la circonferenza per semplificare la trattazione
(intento esplicitamente espresso dagli autori che evidentemente ritengono di troppo difficile comprensione per i quindicenni di oggi la
definizione standard di luogo dei punti equidistanti da un centro), questa "facile" definizione di angolo "si dice angolo convesso l'intersezione
di due semipiani le cui origini hanno intersezione non vuota", seguita dalla seguente osservazione "...un angolo può essere anche pensato
come rotazione. Immagina il movimento della lancetta dei secondi di un orologio [...]"
La parte di piano per lo meno era qualcosa. Ma la rotazione
21
!.....come battere la testa sulla "rotazione" di un tavolo, o aspettarsi alla "rotazione"
di una strada? E soprattutto, dov'è andata a finire la punta? E qui muore la speranza dello studente di poter imparare la matematica in modo
attivo, integrandola con coerenza con le proprie rappresentazioni fisiche e concettuali del mondo.
Si potrebbe obiettare, in un sussulto bourbakista, che la trattazione formale oggi è così ben costruita da mettere in grado, se acquisita,
di portare avanti qualunque argomento in qualunque ambito della matematica, eliminando così il problema dell'intima comprensione. Chi ha vissuto
anni di stretta convivenza con i grossolani e ingenui modelli scientifici del mondo dei nostri adolescenti però sa quanto essi siano attivi,
pressanti e vitali nelle domande che essi all'inizio, nonostante tutto, rivolgono con entusiasmo all'insegnante e come le risposte che non ne
tengano conto smorzino drasticamente la curiosità e l'interesse per la materia. Il danno didattico non si limita solo a questo aspetto
affettivo, ma si estende anche all'autonomia creativa degli alunni nella soluzione dei problemi e alla loro capacità di proporre soluzioni
non standard. In pratica toglie strumenti alla gestione non "scolastica" della matematica.
Cose ineffabili
Ineffabile vuol dire non esprimibile a parole. Le cose ineffabili nella nostra vita sono moltissime e spesso hanno anche un nome. Prendiamo per
esempio le facce: siamo capaci di riconoscere il volto di ogni persona con cui abbiamo a che fare, ma non potremmo mai esprimere verbalmente
l'insieme delle relazioni colte dallo sguardo tra le sue componenti, relazioni che sono le sole a permettere ad ogni volto la propria
unicità. Lo sappiamo fare ma non lo sappiamo dire. Il volto umano è ineffabile. O, se vogliamo calarci nel gnoseologico, la conoscenza
che abbiamo di esso è intuitiva, non razionale
22
.
Di solito le cose ineffabili non sono cose. Il frate Luca Pacioli, descrivendo la sezione aurea
23
, attribuisce a questa "divina proporzione"
caratteristiche di ineffabilità
24
che la accomunano a Dio e al sorriso della Gioconda. Che la proporzione non sia un oggetto
25
nel senso comune
del termine è pacifico, così come non lo è il sorriso, ma spesso il nostro pensiero si sbilancia da quella parte e materializza
impropriamente essenze che dovrebbero rimanere eteree.
Tra le cose ineffabili della geometria possiamo mettere anche l'angolo.
Angolo piano è l'inclinazione reciproca di due linee in un piano, che si toccano e non giacciono in linea retta
Questa definizione, che troviamo negli Elementi di Euclide, che quindi risale al 300 a.c., è il punto di arrivo di una pratica storica
con gli angoli durata qualche millennio, della quale ci sono arrivati documenti e frammenti, pur se con buchi di centinaia di secoli.
La definizione non dice cos'è l'inclinazione
26
(e come si potrebbe?) e lascia che il termine klisiV,
familiare nella lingua parlata, ne restituisca il concetto, ma conferisce all'angolo un aspetto di relazione, piuttosto che di oggetto, aspetto
che credo sia stato fortemente presente agli albori della geometria, quando ancora questa scienza si esercitava come pratica empirica, senza
presupposti e metodi teorici che ne giustificassero i risultati. L'inclinazione non è una cosa concreta, è più astratta di
un pomodoro o di una parte di piano, ma non è per questo meno intuitiva. Il nostro orecchio è dotato di congegni sofisticatissimi
che ci danno costantemente informazioni sullo stato della nostra inclinazione rispetto alla verticale, che correggiamo intuitivamente quando
è il caso. Nel sistema vestibolare dell'orecchio interno abbiamo una singolare riproduzione dei riferimenti cartesiani, XYZ, effettuata
mediante tre canali pieni di liquido, orientati tra loro ad angolo retto, che ci regalano un filo a piombo personale (per questo la verticale
non è vissuta psicologicamente come una "inclinazione" ma come una cosa diversa da essa).
Anche il nostro muoverci nello spazio crea spontaneamente astrattissimi concetti geometrici. Quando tendiamo una mano per cogliere una mela da
un ramo individuiamo un bersaglio
27
, una direzione che guida lo stendere del braccio, e in questa direzione sono allineati la spalla, il gomito,
il polso, l'oggetto. Il braccio allora è dritto, rettilineo, situazione contrapposta all'essere piegato, al formare un angolo
28
, al cambiare
direzione.
Questa situazione si estende naturalmente anche agli oggetti: un bastone è dritto se può essere considerato un'estensione del braccio
steso, cioè se conserva gli allineamenti necessari per raggiungere un corpo. L'essere rettilineo è una condizione cognitivamente molto
forte, e insieme all'essere spezzato guida il nostro muoverci nel mondo e l'individuarvi forme.

L'ombra e le linee spezzate trasformano la figura da poligono piano a forma tridimensionale
fig 11
Gli egiziani di millenni fa, erano impegnati, oltre che nella ricostituzione periodica della forma dei loro campi, anche nel calcolo accurato
di inclinazioni. Il problema 56 del papiro di Rhind
29
, ad esempio, arrivato fino a noi segnato su frammenti di papiro, chiede di calcolare
il "seqt" della faccia di una piramide a base quadrata, alta 250 cubiti, con lato di 360 cubiti. Il "seqt" era la misura egiziana della pendenza
di una linea - l'inclinazione reciproca di due linee diventa la pendenza di una di loro quando l'altra è orizzontale - e veniva ottenuta
misurando in "mani" la profondità corrispondente alla elevazione di 1 cubito, equivalente a sette mani.
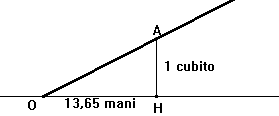
Il seqt era la misura di OH in "mani". Il seqt della linea OA è di 13,65 mani (1 cubito = 7 mani)
fig. 12
La soluzione che troviamo nel papiro è questa: si divide la base per due, e si divide ulteriormente il risultato per 250, per trovare
la profondità in cubiti. Successivamente si moltiplica questi risultato per sette, per esprimerlo in mani. La cosa interessante di
questo problema, al di là della tecnica dei loro calcoli, sta nell'esistenza del concetto di seqt, segno rivelatore della consapevolezza
che la costanza della direzione e la costanza della forma sono legate tra loro. L'inclinazione della faccia della piramide, pensata come una
qualità comune a ogni parte di essa, nel momento della misura si mantiene attraverso il rapporto. L'ipotenusa
30
del triangolo rettangolo
ABC è tesa tra una profondità e una elevazione e la sua inclinazione quindi si può trasferire a piacere.. Il triangolo rettangolo,
attraverso i suoi cateti, segmenti di misura e di inclinazione conosciuta (e cosa di più biologicamente conosciuto dell'essere orizzontale
e dell'essere verticale?) diventa strumento per "comunicare" e trasferire una inclinazione ignota.
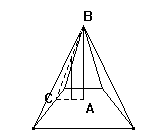
fig. 13
E anche nel caso dell'inclinazione, le forme che la trasmettono si caricano di forti riferimenti pragmatici. Esiste a questo proposito un'interessante
e curiosa testimonianza nel Chou Pei Suan Ching, un antico testo di matematica cinese, attribuito al IV secolo a.C. riguardo al modo di vedere il
triangolo rettangolo secondo l'uso:
Chou Kung esclamò
" Davvero grande è l'arte del calcolo. Mi piacerebbe conoscere il Tao dell'uso del triangolo rettangolo"
Shan Kao rispose
"Il triangolo rettangolo in piano (posto sul terreno) serve a stendere il progetto di (opere) diritte e squadrate (con l'aiuto di ) corde,
il triangolo rettangolo inclinato serve ad osservare le altezze. Il triangolo rettangolo rovesciato serve a scandagliare le profondità.
Il triangolo rettangolo in posizione orizzontale è usato per accertare le distanze."
31
Euclide stesso non riesce del tutto a liberarsi dal vincolo dei riferimenti psicologici e invece di vedere una continuità di specie tra gli
angoli compresi tra 0 e 180 gradi, ne fa rispetto alla verticale
32
una classificazione in tre tipi, l'acuto, il retto e l'ottuso. Osserva
Proclo nei suoi Commenti al I libro degli Elementi di Euclide:
Queste sono le tre specie di angoli, di cui parla anche Socrate nella Repubblica, ammessi dai geometri nell'ipotesi che una linea retta formi
questi angoli secondo una distinzione in specie, cioè la specie retta, l'acuta, l'ottusa [...]
33
La forma si conserva (restringiamoci per semplicità alle figure piane) se nello spezzarsi dei lati, fatto necessario al chiudersi della figura,
si conservano le inclinazioni, cioè gli angoli. Un leggero cambiamento di direzione provoca un sensibile cambiamento di forma, per il nostro
sistema percettivo, soprattutto se avviene relativamente ai riferimenti naturali alto-basso, destra-sinistra.
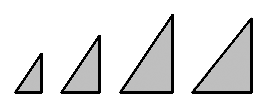
Spicca immediatamente tra gli altri il triangolo con forma diversa,
corrispondente
a una variazione dell'inclinazione dell'ipotenusa di circa 6 gradi
fig. 14
Anche il parallelismo è fortemente intuitivo, prontamente avvertito visivamente. Riusciamo a individuare la figura non simile alle
altre più facilmente in configurazioni nelle quali i lati di quelle simili sono rispettivamente paralleli:
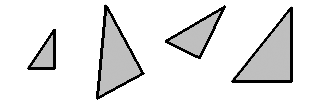
I triangoli sono gli stessi della figura precedente, ma è più difficile individuare
quello "diverso"
fig. 15
Cose curve?
Una cosa che interessa e colpisce molto gli studenti è il fatto che Euclide non pone nella sua definizione la condizione che le linee
inclinate l'una sull'altra siano rette. L'esistenza dell'angolo curvilineo è per gli alunni una scoperta curiosa e può essere
convenientemente sfruttata dal punto di vista didattico perché porta con sé il vantaggio dell'incontaminazione dalle cose della
vita. Non esiste oggi nella pratica niente che si rifaccia all'angolo curvilineo, non esistono parole, immagini, misurazioni, situazioni che vi
facciano ricorso. Questo ne fa una cosa "pulita" dal punto di vista cognitivo, cioè una cosa che non si porta dietro proprietà
presunte, credenze, suggestioni, usi impropri, approssimazioni, che portano in modo acritico a valutazioni sbagliate. Tutto ciò che
riguarda l'angolo curvilineo, non avendo modelli già costituiti a disposizione, impegna il pensiero a confrontarsi con definizioni, enti
e proprietà geometriche in modo attento e rigoroso e solleva problemi di base che investono anche la concezione dell'angolo rettilineo.
Gli angoli curvilinei si incontrano continuamente nella pratica geometrica, ma la mancanza di parole per designarli li rende invisibili. Basta
disegnare una circonferenza, ad esempio, e una sua corda, per ottenere una figura, il settore circolare, con relativi angoli curvilinei

fig. 16
L'esplorazione dei possibili angoli curvi mette subito in evidenza aspetti incongrui con l'idea dell'angolo come parte di piano:

fig. 17
Che succederà all'angolo curvo in figura, come si sviluppa? I lati correranno paralleli (come quelli del ritaglio della buccia di una mela,
mi è stato detto una volta) o si incroceranno?
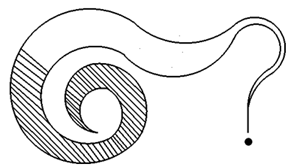
Disegno di un angolo curvilineo visto da uno studente di scuola d'Arte.
fig. 18
Ritornando all'angolo proposto prima, possiamo fornire un contesto più ampio mostrando come ad esempio faccia parte di una lunula
34
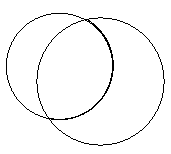
fig. 19
ma anche aggiungere le circonferenze, dare il giusto contesto e levare così di torno la buccia della mela non diminuisce le perplessità:
cosa fa quell'angolo, non continua? è chiuso? come è possibile....? Se si fa loro notare che non si pongono le stesse domande di
fronte agli angoli di un triangolo - e la situazione è del tutto equivalente - protestano: "Ma è un'altra cosa!..."
fig. 20
Hanno ragione. Quando gli angoli si mischiano alle forme, diventano parti delle forme stesse e acquistano psicologicamente il carattere di
oggetto. La visione trasforma immagini retiniche in descrizioni mentali, e nelle descrizioni degli studenti le lunule sono solo ritagli, non
sono oggetti. Nel triangolo l'angolo è "l'angolo del triangolo" (come lo sono, del triangolo, i lati, i vertici, le altezze...) mentre
nella lunula i segni non creano una sovrastruttura emergente, la figura di lunula non si impone e non genera di conseguenza "gli angoli
della lunula". In genere se si parla di angoli e si indica una lunula, non si vede il "biangolo" - tale è la lunula - con i suoi angoli,
bensì un angolo, con una forma che non asseconda coerentemente il suo propagarsi all'infinito, contrariamente a quanto siamo abituati dalla
pratica con l'angolo rettilineo, nel caso del quale l'inclinazione definisce anche una direzione mantenuta dai lati.
Nella situazione curvilinea dunque non si impone una figura e gli angoli tenderebbero ad espandersi nel piano, ma seguendo i loro lati si ha
l'impressione di finire in vicoli ciechi, o in paradossi
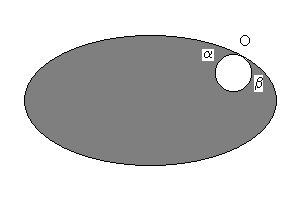
Esistono due angoli curvilinei, a e b,
divertice O, o solo uno?
fig. 21
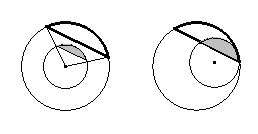
Gli angoli dei settori circolari a sinistra appaiono uguali per motivi di similitudine,ma se sovrapposti
non coincidono
35
fig. 22
Un ultimo esempio riguarda il problema dell'angolo di contingenza, cioè dell'angolo mistilineo formato dalla tangente alla circonferenza
e la circonferenza stessa:
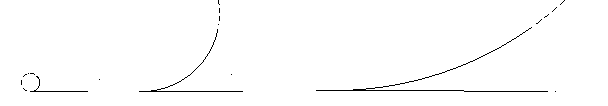
Gli angoli di contingenza sono uguali o formano una successione decrescente?
fig. 23
Gli angoli appaiono diversi mentre con una similitudine, aumentando il raggio del cerchio, potremmo trasformare un angolo nell'altro
36.
La riflessione su questi casi riconduce inevitabilmente alla definizione di angolo come inclinazione reciproca di due linee, e al fatto che
l'inclinazione è una circostanza locale, circoscritta al loro punto di intersezione, che può essere affrontata in maniera abbastanza
elementare per mezzo delle tangenti alle curve stesse. Gli angoli di contingenza inducono anche a interessanti indagini sulla curvatura, che
però si prestano a discussione solo in classi che stiano già affrontando argomenti di analisi.
Indagare sull'inclinazione dei lati di un angolo curvilineo porta ad affrontare, se pur in maniera intuitiva, argomenti di analisi
infinitesimale. Quanto vicino al vertice devo mettermi per poter valutare l'inclinazione? Proclo riporta in proposito l'opinione di Plutarco
37.
"tra coloro che dicono che l'angolo "è il primo intervallo sotto il punto"
38.
e di Apollonio, secondo il quale "l'angolo è la
contrazione di una superficie in un sol punto sotto una linea spezzata."
39.
Queste definizioni enigmatiche e molto suggestive ci riconciliano con la "punta" dell'angolo levando di torno ingombranti e inutili parti
di piano, suggerendo l'idea di identificare l'inclinazione delle linee curve con quella delle loro tangenti condotte nel punto di
intersezione. Tra le diverse possibilità di definire correttamente l'idea di angolo è da privilegiare, secondo noi, quella che
sviluppando i primi modelli intuitivi che si formano spontaneamente nel pensiero, riesce a conciliarsi con gli sviluppi a cui è pervenuta
la matematica nel suo corso storico fino ai nostri giorni.. Nella geometria differenziale per esempio l'idea di angolo tra due curve è
un concetto fondante e di grande utilità. Si tratta di un concetto locale concentrato nel punto dove si avverte una discontinuità
della derivata prima, dove la direzione tangente alla linea cambia bruscamente con un "salto".. Quel punto con quel salto che percettivamente
cogliamo come se lì "accadesse qualcosa" diventa un fatto infinitesimale dato dal mutamento discontinuo di direzione dei due vettori
tangenti ai due rami della linea.
Ci dice Enriques
E come mai la scienza superiore (le matematiche trascendenti e sublimi che abbiamo studiato negli anni dell'università) dovrebbero
ritornare - in qualche modo - a rischiarare la nostra mente proprio mentre stiamo cercando di farci piccoli coi piccoli, sui banchi di scuola?
Rispondo: non vi è iato o scissura fra matematiche elementari e matematiche superiori, perché queste si sviluppano da quelle,
al pari dell'albero dalla tenera pianticina.[...] lo sviluppo dei problemi matematici recherà luce sulle dottrine elementari su cui
essi profondano le loro radici. Ad una condizione però che di ogni dottrina si studi le origini, le connessioni, il divenire, non
un qualsiasi assetto statico; e però che un grado di verità più alto serva ad illuminare il più basso da cui
è uscito; che insomma - dopo aver studiato la scienza - ce ne valiamo per comprendere la storia. Quale modo più largo di
comprensione, quale più vasta esperienza didattica, che l'annodarsi dei problemi e l'urtarsi delle difficoltà entro lo spirito
di tutti gli studenti che hanno faticato prima di noi, nella scuola del mondo?
40.
La qualità delle cose
Gli angoli curvilinei sono definiti dal testo euclideo, ma la trattazione geometrica degli Elementi prende in esame quasi esclusivamente gli angoli
rettilinei. Perché?
Proclo ne fa una questione di qualità, cioè di forma: l'angolo "richiede anche la qualità secondo la quale esso ha anche una
forma sua propria e un suo tipo di esistenza "
41.
. Gli angoli rettilinei e curvilinei sono di diversa qualità, e questo crea dei problemi
perché l'angolo generico " [...] possiede una sua qualità particolare, per la quale i suoi angoli sono spesso non paragonabili
tra loro "
42.
Durante la discussione sul postulato IV del libro I: "E che tutti gli angoli retti siano uguali tra loro", Proclo mostra attraverso alcuni problemi
le difficoltà nel gestire insieme angoli curvilinei e rettilinei. Questo postulato, osserva Proclo, è verificato solo dagli angoli
rettilinei. Osserviamo per esempio la seguente situazione:
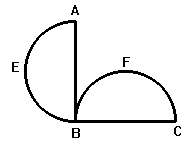
fig. 24
Siano AB e BC due segmenti uguali e perpendicolari in B e siano costruiti su di essi due semicerchi, AEB, BFC, con lo stesso raggio. Poiché
i due semicerchi sono uguali per congruenza, l'angolo EBA è uguale all'angolo FBC. Abbiamo che l'angolo retto ABC è formato dagli
angoli ABF e FBC ed è quindi uguale all'angolo lunulare EBF - formato da EBA e ABF - che però non è rettilineo ed è
perciò diverso da esso per qualità.
Questa "uguaglianza imperfetta " si verifica anche per gli angoli acuti e ottusi
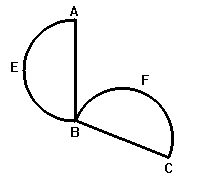 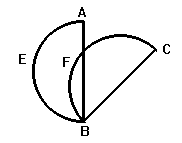
fig. 25
L'angolo lunulare EBF "è uguale" all'angolo rettilineo ottuso ABC perché somma di parti uguali, analogamente a quanto visto prima, mentre
l'angolo lunulare EBF "è uguale" all'angolo acuto ABC per differenza di parti uguali: ABC = FBC - FBA = EBA - FBA = EBF
Questo argomento, legato all'intuizione della forma, in realtà non è fondamentale per l'esclusione degli angoli curvilinei
dalla teoria euclidea. Il motivo principale di tale esclusione risiede nel fatto che gli angoli curvilinei e rettilinei, una volta che
si sia chiarito il modo di confrontarli, sembrano non formare un insieme archimedeo, cioè non soddisfare il postulato di Archimede,
di basilare importanza per la teoria delle proporzioni tra grandezze, enunciato nel postulato IV del libro V: "Si dice che hanno tra loro
rapporto (o ragione) le grandezze le quali possono, se moltiplicate, superarsi reciprocamente". Proclo osserva a questo proposito:
Ora, le cose che hanno rapporto fra loro possono oltrepassarsi una con l'altra quando vengano moltiplicate; dunque l'angolo cornicolare
43.
oltrepasserà una buona volta l'angolo retto, il che è impossibile; perché è dimostrato che l'angolo cornicolare
è minore di ogni angolo rettilineo.
44.
Nella proposizione III,16 Euclide dimostra in effetti che non esiste nessun sottomultiplo di un angolo rettilineo che sia minore dell'angolo
di contingenza, presupponendo quindi nell'uso del termine "minore" un possibile confronto tra due "qualità" diverse. Se dunque,
influenzati dalla forma, supponessimo l'angolo di contingenza non nullo, il Postulato di Archimede non sarebbe soddisfatto.
Il dito e la luna
La storia dell'angolo lo vede prendere corpo in vari modi, a seconda dell'ambito in cui è usato. Euclide è noto soprattutto per gli
Elementi, ma questa opera fortunata non è la sola a cui il mondo scientifico ha fatto riferimento. Fino al Rinascimento infatti era
conosciuto e studiato come testo classico anche la sua "Ottica", opera che si occupa della visione diretta inquadrandola in uno schema geometrico,
fedele a una rigorosa impostazione assiomatico-deduttiva
45.
.
L'Ottica si fonda su una nozione basilare, quella di "angolo visivo", per mezzo del quale vengono date le regole che descrivono il mondo "come si
vede". La scenografia e la rappresentazione prospettica all'epoca si basavano su tali regole, ma il concetto di angolo visivo aveva una sua
origine ancora più lontana, legata all'osservazione astronomica. In questo ambito l'angolo trova storicamente una sua dimensione poetica a
grandiosa se pensiamo che fu lo strumento fondamentale per l'osservazione e la metrica del cielo, in tempi in cui la geometria piana era ancora
nella sua fase iniziale. Il "guardare", questo semplice atto percettivo, esce così dal vissuto particolare della storia del singolo individuo
e entra nel quadro storico del pensiero scientifico come strumento di misura.
Nell'ottica antica, la visione era legata all'insieme dei raggi visivi uscenti dall'occhio e formanti un angolo (visivo). Tolomeo, che riprenderà
in una versione critica e ampliata questioni riguardanti la visione, scrive un manuale sull'Ottica definendo l'angolo visivo come quello descritto
dall'insieme continuo
46.
dei raggi visivi uscenti dall'occhio fino all'oggetto sotteso. Questa definizione può aver suggerito nel tempo, come
possibile modello di angolo, un fascio continuo di raggi lineari uscenti da un centro comune.
Mi sembra che possiamo ritrovarne un'eco nella definizione che nel 1900 Amaldi accolse in un suo articolo
47.
sui concetti di retta e piano. Amaldi
prende in considerazione la definizione di angolo come parte di piano racchiusa da due raggi uscenti da un punto
48.
e le contesta di non
corrispondere completamente al concetto intuitivo di angolo. Quando si danno due raggi a, b, uscenti da un punto O, dice, si definiscono
due figure geometriche distinte: la parte di piano limitata dai due raggi, o insieme bidimensionale dei punti che giacciono tra a e b, e
la parte del fascio di raggi di centro O che è limitata da a e b, o insieme a una dimensione dei raggi uscenti da O e compresi fra a e b.
Il nostro concetto intuitivo di angolo, conclude Amaldi, si identifica piuttosto con quest'ultimo ente a una dimensione che non con la
regione piana compresa fra i due raggi.
Come è approdata allora nei nostri testi scolastici di geometria la definizione di angolo come parte di piano? Non lo so, ma certamente
Amaldi propone di non identificare l'angolo con la porzione di piano che individua e invita a designare la parte di piano compresa tra i lati
dell'angolo col nome di "regione piana angolare"
49.
proprio per evitare confusione tra i due oggetti geometrici. Evidentemente poi, invece,
nonostante l'autorevole esortazione, è rimasta in uso nella nostra scuola la definizione settecentesca che non distingue tra regione angolare
e angolo.
Come si vede, tutta la questione riguardante gli angoli è notevolmente ingarbugliata.
Io personalmente preferisco pensare all'angolo come inclinazione, anche se tutte le volte che indico una forma intendendo mostrare
un'inclinazione mi sento come quello che, indicando col dito il cielo, ottiene solo di avere tutti gli occhi puntati sul suo dito invece che
sulla luna. Sono inoltre leggermente ossessionata dalla dimensione. Perché l'angolo deve averne per forza una, visto che l'attribuzione
non è né semplice né necessaria? La domanda è aperta, chi volesse rispondere è ben accetto.
Mi si dice "ma è una grandezza!". Anche il numero è una grandezza, ma vive molto bene anche senza dimensione. Oppure si dice
che all'angolo appartiene la bidimensionalità perché è divisibile in due parti da una linea
50.
, ma quello che viene diviso
non è una inclinazione bensì una forma piana i cui contorni rispettano tale inclinazione!
Leggendo di queste questioni mi perdo sempre un po'. È come se ti mostrassero un corpo in movimento intendendo mostrare la sua velocità
e finissero per parlarne come se fossero la stessa cosa. Mi rifugio, come compromesso, nella formale definizione hilbertiana, di angolo: Si chiama
angolo il sistema di due qualsiasi semirette distinte h,k in un piano, aventi origine in uno stesso punto O e appartenenti a rette diverse"
51.
che,
pur suggerendo un corpo, per lo meno non gli attribuisce nessuna dimensione.
Il mio personale invito, a scuola, è quello di lasciare all'angolo la sua ineffabilità e di definirlo con Euclide come inclinazione
tra due linee uscenti da un punto, pur con una discussione sul concetto di "angolo" nella storia della matematica e nella pratica
della vita.
In tutta la filosofia ellenistica, come è noto, era ben distinto il piano della realtà da quello della logica e della conoscenza, ma
la costruzione del sapere scientifico, pur essendo autoconsistente, avveniva fondamentalmente in accordo con la realtà sensibile. Si trova
testimonianza di questo fatto proprio nel modo in cui sono dati i principi fondanti degli Elementi. Euclide, a differenza di quanto si fa oggi,
definisce tutti gli enti matematici dei quali si occuperà nella sua opera, e definisce quindi anche tutti gli enti primitivi, perché
si presupponeva che gli enti da definire fossero una qualche idealizzazione di un corrispondente sensibile e quindi riconoscibili attraverso
una descrizione
52.
. Il modo storicamente più antico di concepire la definizione come descrizione pare anche quello più naturale per
il pensiero non educato scientificamente. Il passaggio da questa concezione a quella più avanzata che porta in sé l'idea di sistema
formale moderno è delicato e spesso negli alunni si compie in maniera incompleta o non si compie affatto se non avviene secondo le tappe
opportune.
Vorrei finire come ho cominciato, con le parole di Enriques:
Ho avuto la fortuna di assistere a qualche lezione di aritmetica o di geometria pratica, in cui il discente si metteva a conversare coi ragazzi
facendosi - anche lui - un poco ignorante, ricercando insieme con loro, suggerendo, a tentoni, la via che essi stessi dovevano percorrere per
guadagnare la verità. E [...] mi chiedevo perché lo stesso metodo non si dovesse adoperare anche con alunni di età
più matura...perché no?, anche coi giovinotti che vengono a studiare alle nostre università. [...] Il più gran vantaggio
di questo metodo è, a mio avviso, la sincerità, perché il postulato dell'ignoranza è infinitamente più vicino al
vero che la presupposizione di conoscenze già sicure nell'allievo, da cui muove la lezione cattedratica. [...] Ma per ciò occorre
che anche noi maestri - nell'atto di insegnare - ripetiamo, non già il resultato freddo degli studi fatti, bensì il travaglio
interiore per cui riuscimmo a conquistare la verità [...]Vorrei spiegarmi bene su questo punto: la fatica di cui parlo è reale,
non finzione ad uso didattico; infatti non è possibile che ripensiamo una difficoltà che una volta abbiamo vinto, senza scoprire
nello stesso problema qualche altra difficoltà che si risolve in una comprensione nuova e più alta; perché è falso
che le cose elementari su cui torniamo per insegnarle sieno facili al confronto della scienza superiore il cui possesso ci rende oggi
orgogliosi davanti ai nostri scolari; perché infine codesto possesso medesimo è dubbio e vano, ridicolo l'orgoglio, se di fronte
al discepolo ci presentiamo soltanto come discepoli, a ripetere un po' più meccanicamente la vecchia lezione appresa sugli stessi banchi,
anziché come maestri, a cercare una veduta nostra, più chiara e più larga.
53
Bibliografia
Amaldi U., Sui concetti di retta e piano, in Questioni riguardanti le matematiche elementari, Parte prima, raccolte e coordinate da F.Enriques, Zanichelli, 1983
Boyer C.B, Storia della Matematica, Mondadori, Milano, 1980
Bruner J., Verso una teoria dell'istruzione, Armando Editore, Roma, 1967
Casati R., La scoperta dell'ombra, Mondadori, Milano, 2000
Catastini L., Il pensiero allo specchio, La Nuova Italia, Firenze, 1990
Catastini L., Neuroscienze, apprendimento e didattica della matematica, Progetto Alice, vol II n° 6, 2001
Catastini L.,Ghione F., La geometria della visione: dall'Ottica di Euclide alla prospettiva rinascimentale, in Matematica, Arte, Tecnologia, Cinema, a cura di M.Emmer, M.Manaresi, Springer, Milano 2002
Enriques F., Insegnamento dinamico, Periodico di Matematica, Serie IV, Vol. 1, 1921
Enriques F., Gli Elementi di Euclide e la critica antica e moderna, libri I-IV, Stock, 1925
Euclide, Gli Elementi, a cura di A. Frajese e L. Maccioni, U.T.E.T, Torino, 1970
Ghione F. Divina Proportione, CD-ROM Hochfeiler, Roma, 1999
Hilbert D., Fondamenti della geometria, con i supplementi di P.Bernays e introduzione di C.F. Manara,, Feltrinelli, Milano 1970.
Jullien V. (par), Éléments de géométrie de G. P. de Roberval, Vrin, Paris, 1996
Kline M., La matematica nella cultura occidentale, Feltrinelli, Milano 1976
Maffei L., Mecacci L., La visione, Mondadori, Milano, 1979
Needham J., Scienza e civiltà in Cina, Volume terzo, Parte prima, Einaudi, Torino, 1985
Pinker S., Come funziona la mente, Mondadori, Milano, 2000
Proclo, Commento al I libro degli Elementi di Euclide, a cura di M.Timpanaro Cardini, Giardini Editori, Pisa, 1978
Timpanaro Cardini M., I pitagorici, fasc. II, La Nuova Italia, Firenze, 1962
Tolomeo C., L'ottica, a cura di G.Govi, Torino, 1885
Wertheimer M., Il pensiero produttivo, Giunti, Firenze, 1965
Wittgenstein L., Osservazioni sulla filosofia della psicologia, Adelphi, Milano, 1990
| |