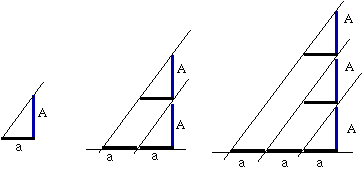Indice

Le equazioni lineari

2. La falsa posizione: due antichi problemi di geodesia.
La piramide, l'ombra, il bastone

     

A Talete è attribuita la soluzione di alcuni problemi di geodesia:

Determinare l’altezza di una piramide conoscendo l’ombra che essa proietta.

Su questo ci sono notizie contraddittorie. La misura è stata fatta realmente o si tratta di una leggenda? Per piramide si deve intendere obelisco? (perché altrimenti la base potrebbe essere troppo grande e coprire in parte l'ombra rendendo complicato il calcolo).
Diogene Laerzio riferisce (sulla base di una testimonianza scritta, oggi perduta, di un allievo di Aristotele) che Talete avrebbe misurato l’altezza della piramide guardando la sua ombra nel momento in cui i raggi del sole sono inclinati di 45 gradi.
D’altro lato Plutarco nel Banchetto dei sette saggi, fa dire a Nilosseno, rivolgendosi a Talete, quanto il re lo ammiri:

Benché egli ti ammiri anche per altre cose, pure egli pregia sopra tutte la misura delle piramidi, giacchè tu senza fatica alcuna e senza ricorrere ad istrumenti, ma col solo infliggere il bastone all’estremo dell’ombra proiettata dalla piramide, hai dimostrato, servendoti dei due triangoli risultanti dal contatto col raggio luminoso , che un’ombra ha all’altra lo stesso rapporto che la piramide al bastone.

La versione di Plutarco sembra presupporre che Talete conoscesse la teoria della similitudine cosa che molti storici mettono in discussione come l’attribuzione del "teorema di Talete" sul fascio di rette parallele tagliate da una trasversale.
Nel libro citato in bibliografia Il teorema del pappagallo (pp 41-63) si trova una interessante ricostruzione romanzata di questa eventuale, mitica, misura che potrbbe essere utile, anche dal punto di vista didattico, per introdurre l'idea di similitudine.

click per ingrandire la figura
Talete di Mileto

Noi invece cercheremo di ricostruire, prendendo spunto da questo problema e dalla osservazione delle ombre, un possibile cammino verso la teoria delle proporzioni a prescindere dalla mirabile trattazione di questo argomento dovuta a Eudosso ed esposta nel V libro degli Elementi di Euclide. La strada che cercheremo di seguire si colloca in quella fase dello sviluppo del pensiero razionale che noi chiamiamo prescientifico dove ancora non è chiara la distinzione tra modello teorico e realtà oggettiva che col modello si vuole descrivere 1 e dove le dimostrazioni mischiano evidenze empiriche con verità teoriche e ragionamenti filosofici non ancora perfettamente chiariti. Sarà solo con Aristotele che la Logica prenderà la forma di un codificato ed universale sistema di ragionamento e con Euclide il metodo assiomatico deduttivo, proprio di un pensiero scientifico maturo, riuscirà, per la prima volta, ad organizzare l'insieme delle "verità" geometriche note in un sistema coerente dove i presupposti sono postulati in modo chiaro e i teoremi dedotti con le regole universali della logica aristotelica. La bellezza e la potenza di quest'opera ha, in un certo senso, oscurato altre strade, scartato altri tentativi presenti, crediamo, in un pensiero non ancora completamente maturo, ma comunque capace di animare quel contesto nel quale la formalizzazione euclidea ha potuto poi prendere forma. Il metodo di induzione matematica, ad esempio, non trova nella sistemazione aristotelica e poi in Euclide una formalizzazione soddisfacente e viene quindi escluso come metodo dimostrativo mentre lo ritroviamo, anche se in modo rozzo, nello studio dei numeri figurati di origine pitagorica e anche in un passo del Parmenide di Platone 2. Naturalmente la mancanza quasi totale di testimonianze dirette rende la nostra trattazione priva di un valore storico documentato, ma crediamo, contribuisce a delineare uno dei possibili sviluppi del pensiero matematico coerente coi pochi dati a disposizione.
L'utilità didattica di una ipotetica ricostruzione degli albori del pensiero scientifico dove gli attori sono uomini che indagano la natura con mezzi minimi sia pratici che teorici, consiste anche nel fatto che quei personaggi, quelle forme iniziali di ragionamento razionale sono analoghe a quelle che ritroviamo nei giovani che si accostano, sprovveduti, a un pensiero scientifico come se il percorso storico riproponesse in grande lo sviluppo del pensiero nell'individuo.

 Il pensiero prescientifico

Comunque siano andate le cose, l'osservazione delle ombre può essere stato un potente stimolo, e lo sarà anche per noi, per sviluppare qualche riflessione sull'idea di proporzionalità o meglio su quella di operatore lineare che ne evidenzia la natura profonda: possiamo, per cominciare, pensare il "fare ombra" come un operatore che a un oggetto verticale X (ad esempio un obelisco) associa la sua ombra ombra(X).
Questo operatore ha due importanti proprietà:

     (i) l'operatore conserva i multipli interi, cioè: se X raddoppia, le sue dimensioni anche l’ombra di X raddoppia, se X triplica anche l’ombra triplica ecc. In formule

ombra(nX) = n ombra(X)   per ogni intero positivo n.

    (ii) l'operatore è crescente cioè se A è più grande di B anche l'ombra di A è più grande dell'ombra di B.

Queste proprietà possono essere verificate facilmente sulla base dell'esperienza comune stabilendo un rapporto, non più solo analogico, ma anche quantitativo, tra un oggetto inaccessibile (l'obelisco verticale) e una sua rappresentazione isomorfa (l'ombra orizzontale).

Il problema di trovare l'altezza incognita X dell'obelisco, a partire dalla sua ombra a, è ora quello di invertire l’operatore, cioè di risolvere l’equazione

ombra(X) = a

dove a è un valore noto calcolabile.

 L'operatore "ombra"

Questa equazione che, come vedremo è lineare, puó essere risolta usando il così detto metodo della falsa posizione (che si pensa di origine orientale, forse cinese) che si fonda sulla teoria delle proporzioni.
Prendiamo un bastone B (la falsa posizione) di cui conosciamo la forma, posizioniamolo in modo analogo all'obelisco cioè verticale, calcoliamo la lunghezza della sua ombra e supponiamo di ottenere il valore b: cioè

ombra(B) = b

Se ora l'ombra a di X fosse 2 volte, 3 volte, diciamo n volte, l'ombra b del bastone, allora, per le proprietà (i), avremmo

ombra(X) = a = nb = n ombra(B) = ombra(nB)

e, stabilendo l'operatore una corrispondenza biunivoca per la proprietà (ii), potremmo concludere dicendo che X = nB cioè che l'obelisco è alto come n bastoni messi in fila. In altre parole, l'ombra, cioè l'operatore (lineare come vedremo), crea una analogia, (nel senso etimologico del termine ana-logos) stabilendo che il rapporto che lega X al bastone è lo stesso del rapporto che lega l'ombra di X è all'ombra del bastone.

X : B = ombra(X) : ombra(B).

 Il metodo della
falsa posizione

Si potrebbe obiettare che solo per un caso fortuito abbiamo trovato l'ombra della piramide multipla intera dell'ombra del bastone mentre in generale dobbiamo aspettarci un certo resto. Potrebbe cioè capitare che

nb < a < (n+1)b    cioè    a = nb +c    con    c < b

ma, dato che abbiamo supposto l'operatore crescente, avremo analogamente

nB < X < (n+1)B    cioè    X = nB + C

con C più piccolo del bastone, e il problema è ridotto a vedere come C (che non conosciamo) si rapporta al bastone B (che conosciamo). Ma per questo possiamo ancora riferirci alle ombre: possiamo vedere quante volte c entra in b. Se c entra in b esattamente m volte, cioè se    b=mc, allora poiché l'operatore conserva i multipli interi avremo anche    B = mC, e C risulterebbe la m-esima parte del bastone e in definitiva l'obelisco sarebbe alto come n bastoni messi in fila più un ulteriore pezzetto grande come l'emmesima parte del bastone. Se poi c non entrasse esattamente m volte in c ma ci fosse un resto, se cioè risultasse

b = mc + d    con    d < c

avremo anche

B = mC + D    con    D < C

e potremmo confrontare, guardando le ombre, i resti. In questo modo possiamo approssimare il rapporto X : B nello stesso modo con cui approssimiamo ombra(X) : ombra(B). Quì intendiamo per rapporto A : B un metodo, una procedura di pensiero, attraverso la quale è possibile descrivere la grandezza di un termine conoscendo quella dell'altro.

 Le divisioni successive
per approssimare
un rapporto

La cosa può essere formalizzata nel seguente teorema la cui dimostrazione segue essenzialmente l'idea che abbiamo esposto.

Teorema
Sia


un operatore crescente tale che O(nX) = nO(X) per ogni intero positivo n. Sia B un fissato numero reale positivo (la falsa posizione) allora

X : B = ombra(X) : ombra(B).

per ogni X.

Questo teorema la cui validità intuitiva ha una base fortemente empirica, legata alla osservazione delle ombre, non è di facile dimostrazione se non all'interno di un quadro teorico ben fondato dove una buona definizione di uguaglianza di rapporti consenta lo sviluppo di una dimostrazione rigorosa. La definizione che si fa risalire a Eudosso, riportata nel V libro degli Elementi (definizione 5) di Euclide si adatta molto bene alla nostra situazione poiché l'uguaglianza di due rapporti è ridotta a un confronto tra multipli interi e questo confronto, proprio per le proprietà che ha il nostro operatore, si conserva assieme ai multipli considerati.
Una definizione di uguaglianza di rapporti diversa da quella proposta da Euclide e per un verso più naturale, si basa, come abbiamo accennato nella "dimostrazione" del teorema, sul confronto delle grandezze, la più grande con la più piccola, iterando questo processo ai resti che via via si presentano e imponendo che i risultati siano gli stessi per i due rapporti. Anche questa strada può essere seguita per sviluppare correttamente la teoria dei rapporti e della similitudine, ma non riteniamo utile farlo in questa sede. Osserviamo solo come un ingrediente importante in questa direzione è il metodo di induzione matematica che potrebbe essere utilmente introdotto nella scuola, anche a diversi livelli, a partire da quello ingenuo usato dai pitagorici nello studio numeri figurati. Si considera l'enunciato nel caso n=1, si fa vedere come si passa da n=1 a n=2, si fa vedere che con lo stesso ragionamento si può passare dal caso n=2 al caso n=3 e poi da n=3 a n=4 e così via. Il pensiero afferra il senso di questo metodo e il ragionamento, anche se non formalizzato, risulta assolutamente convincente in tutti gli infiniti casi in cui l'enunciato si presenta.

Esprimendo la tesi del teorema invece che in termini di rapporti, in termini di rettangoli equivalenti, cioè, come prodotti, abbiamo O(X) = k X dove

è una costante indipendente dalla scelta di B. In particolare l'operatore è lineare, e la X compare al primo grado.

 Il teorema principale

Questo teorema è molto importante perché riduce la verifica della linearità dell'operatore, alla verifica di due proprietà essenzialmente qualitative come l'essere crescente e conservare i multipli interi, mentre il teorema permette, da quelle, di ottenere delle informazioni quantitative anche molto precise, riducendo molti problemi ad equazioni del tipo kX = a, cioè di primo grado. La stessa proprietà di conservare i multipli interi poteva (almeno in piccolo) essere assunta con una certa disinvoltura e verificata nei primi casi per n=2, 3. D'altra parte oggi sappiamo che qualunque funzione derivabile, può essere (in piccolo) linearizzata confermando l'enorme generalità di questa impostazione.

L'importanza del teorema

Questi metodi si possono applicare, spingendo come vedremo, più avanti il livello di astrazione matamatica, anche per risolvere un secondo problema di geodesia che pare sia stato pure risolto da Talete:

Determinare la distanza di una nave dal porto

Proclo sostiene che Talete risolse questo problema usando il secondo criterio di uguaglianza dei triangoli, che dunque, come abbiamo detto nel capitolo precedente, doveva essere ben noto: due triangoli che hanno uguali due angoli e il lato compreso sono uguali (Euclide, Libro I, teorema XXVI).
Si puó ipotizzare che se in A si trova il porto, in B un osservatorio in grado di misurare l’angolo visivo b , conoscendo la distanza AB (porto-osservatorio) e supponendo la nave "di fronte" al porto (cioè l'angolo in A retto), allora la sua distanza é univocamente determinata per il teorema citato e puó essere calcolata essenzialmente con lo stesso metodo con cui veniva misurata l’altezza di una piramide a partire dall’ombra.

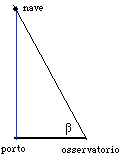
La nave, il porto

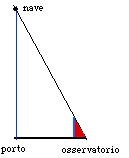
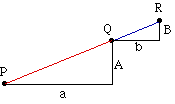
Il metodo a noi pare concettualmente identico: si costrisce una situazione analoga in piccolo in modo che per quella, sia possibile effettuare le misure necessarie: il triangolo rosso nella figura seguente, il segmento azzurro che rappresenta il "bastone", il raggio visivo che traguarda la nave.

I raggi del sole che realizzavano l'operatore ombra vengono sostituiti da raggi visivi e il piano, dove le ombre potevano essere misurate, viene sostituito da un piano artificiale, da una opportuna apparecchiatura dove l'operatore possa lasciare una traccia misurabile.

È questo un processo di astrazione non ovvio e di grande portata: i raggi del sole si vedono e anche le ombre mentre ora si parla di "raggi visivi" di oggetti teorici che non hanno una "realtà" sensibile. Questi raggi visivi sono rette (o semirette) come sarà chiaramente postulato nell'Ottica di Euclide, un'altra opera, meno conosciuta, ma di grande rilievo del geometra alessandrino. L'allineamento di tre punti, l'origine dell'idea stessa di retta, può essere rintracciata in questo riferimento al vedere, al fatto, come dirà Aristotele 3 che il punto intermedio è coperto alla vista dagli altri due. Viene anche studiato uno strumento di enorme utilità in tutti i rilievi geodetici o astronomici che consente di traguardare un oggetto lontano allineandolo, tramite il raggio visivo, a due punti disposti su un'asta rigida, "mirando" come si fa con un fucile. L'oggetto teorico, invisibile, il raggio visivo permette da un lato di sviluppare in senso astratto e rigoroso una "geometria della visione", l'Ottica, dall'altro consente di progettare muovi strumenti che di quella teoria sono conseguenza, coi quali poter descrivere quantitativamente oggetti reali anche molto complessi come, ad esempio, i pianeti e i loro movimenti.

 I raggi visivi

Strumenti di questo tipo, in grado di traguardare, ne esistono diversi tutti essenzialmente equivalenti.
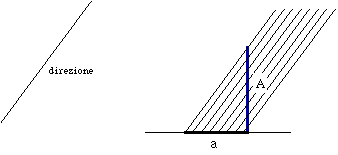
Noi descriviamo, in nota, "lo squadro" che si trova normalmente sul retro di un astrolabio 4.

La considerazione del raggio visivo, proprio perché astratta non è più sufficiente per verificare che l'operatore, analogo all'operatore ombra, conserva i multipli interi. Nel caso delle ombre ci si poteva accontentare di una spiegazione empirica, basata sulla semplice e quotidiana osservazione del fenomeno, mentre ora gli ogetti con cui trattare sono entità astratte.

La considerazione stessa dell'operatore richiede un livello di astrazione maggiore: potremmo dire che, assegnata una direzione, l'operatore trasforma un segmento verticale A nella sua proiezione orizzontale    a    ottenuta seguendo la direzione assegnata.

Questa trasformazione, che in un qualche modo simula la proiezione solare, si fonda sul concetto teorico di parallelismo (stessa direzione) il quale si porta dietro una serie di risultati sugli angoli e sui triangoli dei quali abbiamo palmato il capitolo precedente. È proprio di questa geometria che ci possiamo ora servire per verificare in astratto che l'operatore O che proietta conserva i multipli interi. La "dimostrazione" che proponiamo è ancora una dimostrazione per natura, fondata su una induzione ingenua e molto simile al modo dei pitagorici di trattare i numeri figurati.

Osservando la figura e ricordando che i parallelogrammi hanno i lati uguali, la dimostrazione del teorema risulta evidente.

O(A) = a    O(2A) = 2a = 2O(A)    O(3A) = 3a = 3O(A)
e così via

Questa semplice verifica, unita al fatto evidente che l'operatore O è crescente, permette di concludere che, se tre punti P, Q, R sono allineati, cioè se i raggi PQ e QR sono paralleli allora, applicando il nostro teorema



A : B = a : b

che corrisponde al risultato principale sulla similitudine.

La proiezione parallela

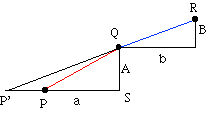
Notiamo anche che, con un semplice ragionamento per assurdo, possiamo ricavare un criterio teorico della massima importanza per stabilire se tre punti sono allineati. Basterà scrivere i rapporti A : B e a : b e vedere se sono uguali. Se questo accade i tre punti sono allineati perché altrimenti prolungando la retta QR fino ad incontrare in P' l'orizzontale PS


essendo R, Q, P' allineati, per quanto già sappiamo avremmo A : B = a' : b    dove a' è ora il segmento SP'. Poiché un rapporto è un modo univoco per calcolare un termine in funzione dell'altro, il termine A è ottenuto da B secondo una data procedura che è la stessa con la quale troviamo a a partire da b, essendo per ipotesi A : B = a : b. Ma anche a' sarebbe, con la stessa procedura, ottenibile da b perché abbiamo visto che A : B è anche uguale ad a' : b e questo, se a' è diverso da a è assurdo.

 Un criterio di allineamento

Notiamo che questo criterio permette di tradurre in termini algebrici (cioè di rapporti) il fatto geometrico (il parallelismo di PQ con QR) relativo all'allineamento di tre punti. Questo ha indotto a definire l'allineamento solo in termini di rapporto trascurandne l'origine geometrica e il legame profondo, che passa attraverso la similutudine, tra questi due fatti. Il fatto che l'equazione cartesiana di una retta sia di primo grado diventa quindi la definizione stessa di retta. Non c'è nulla di cui meravigliarsi, nulla di meraviglioso, nel fatto che l'allineamento si traduca nell'uguaglianza di rapporti poiché, non ci sono due mondi che si collegano con un inaspettato ponte perché quello geometrico, fondato sui postulati di Euclide, viene nascosto. Si fa finta di riferirsi a una entità geometrica a una "linea retta" la quale, spogliata del suo alone di significati, diventa solo una parola, un sinonimo: lineare = di primo grado.

Questa frattura crediamo possa essere alla base di una difficoltà di collegare mentalmente i due concetti (quello di linea retta sepolto in un lontano e vago immaginario geometrico) e quello algebrico staccato sostanzialmente da qualunque rapporto col mondo sensibile.
Queste figure che paiono impossibili e contraddittorie perché le vediamo solo come figure, sono credo la migliore prova di questa situazione di scollamento.


Ringrazio la Dott.ssa Maria Antonietta Fortuna, specializzanda SSIS, per averci segnalato questo finto paradosso, sollecitata a rispondere alla domanda che molti allievi ci rivolgono: è ovvio, lo vedo, perché dimostrare?

Importanza di unire la
Geometria con Algebra
 

Stampa