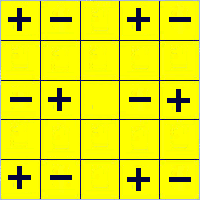
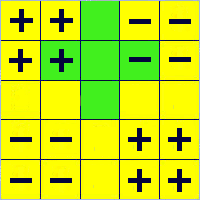
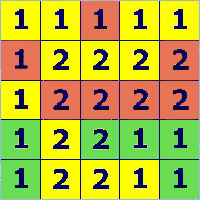
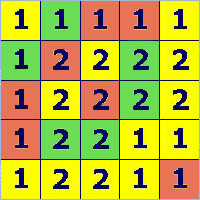
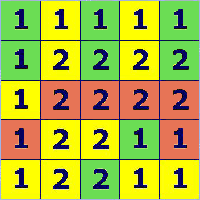
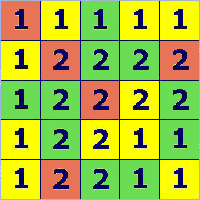
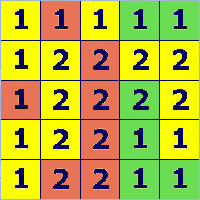
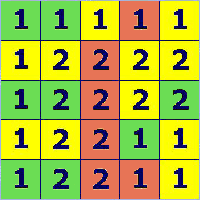
Prima di dare la soluzione facciamo alcune considerazioni di carattere generale. E' interessante osservare che NON e' importante l'ordine in cui vengono eseguiti i click. Inoltre e' sufficiente cliccare ciascuna casella al massimo due volte (cliccarla tre volte equivale a non cliccare affatto).
Quindi per vedere se una tabella è annullabile basterebbe esaminare tutte le combinazioni di click che, per le osservazioni fatte, sono 3 per per ognuna delle 25 caselle per un totale di 3^25=847288609443. Utilizzando la procedura di riduzione che e' spiegata piu' avanti, ci si puo' ridurre all'esame esaustivo di solo 3^5=243 combinazioni. Seguendo questa idea, ALESSANDRO LOFFREDO ha sviluppato un programma in php che permette di verificare se una tabella data e' annullabile e, nel caso lo sia, visualizza tutte le 3^3=27 possibili soluzioni ordinandole per numero di click (il fatto che se ci sono soluzioni queste siano sempre 27 non e' ovvio e verra' spiegato piu' avanti). Il programma puo' essere utilizzato on-line da QUI (il codice php si puo' leggere QUI).
Anche per "soli" 243 casi il metodo esaustivo non e' praticabile senza l'ausilio di un calcolatore. Per risolvere "a mano" i problemi dati seguiremo quindi un'altra strategia basata su degli INVARIANTI ossia delle funzioni che dipendono dalla disposizione iniziale dei numeri nella tabella e che rimangono costanti qualunque casella venga cliccata (cliccando la tabella cambia, ma queste funzioni danno sempre lo stesso valore).
I tre invarianti che prenderemo in considerazione sono i seguenti:

Ogni invariante si calcola facendo la somma dei numeri delle caselle con il segno "+" meno la somma dei numeri delle caselle con il segno "-" e riducendo il risultato modulo 3.
Per verificare che siano effettivamente degli invarianti basta vedere se cliccando su ciascuna delle 25 caselle il loro valore rimane costante. A titolo di esempio vediamo la verifica del primo invariante. Vista la simmetria dell'invariante e' sufficiente controllare 6 casi:

Come si vede, in ogni caso i numeri dei "+" meno i numeri dei "-" delle caselle interessate dall'operazione (quelle verdi) danno sempre 0 modulo 3 e quindi non incrementano ne' diminuiscono il valore iniziale dell'invariante (qualunque esso sia!).

Ora dimostreremo che la tabella si puo' annullare se e solo se TUTTI E TRE GLI INVARIANTI DANNO 0 MODULO 3.
Che questa condizione sia NECESSARIA e' abbastanza chiaro: se la tabella inizialmente ha uno degli invarianti diverso da zero allora, qualunque sia la combinazione di click, questo invariante rimarra' diverso da zero mentre la tabella con tutte le caselle zero ha tutti gli invarianti nulli.
Ora proviamo che la condizione e' anche SUFFICIENTE. Per semplificare il ragionamento conviene prima applicare alla tabella la procedura di RIDUZIONE: si annullano le caselle della PRIMA riga cliccando sulla SECONDA, quindi si annullano le caselle della SECONDA riga cliccando sulla TERZA, poi si annullano le caselle della TERZA riga cliccando sulla QUARTA e infine si annullano le caselle della QUARTA riga cliccando sulla QUINTA.
A questo punto la tabella e' stata annullata tutta tranne l'ultima riga. Le combinazioni che si possono trovare nell'ultima riga sono in tutto 3^5=243 (3 possibilita' per ciascuna delle caselle). Esaminandole si vede che le uniche combinazioni che annullano tutti gli invarianti sono 9 e sono elencate qui sotto. Ciascuna e' effettivamente annullabile e accanto trovate l'indicazione di come azzerare tutta la tabella. Il tasto RISOLVI che trovate in alto funziona proprio seguendo lo schema di questa dimostrazione (il tasto RANDOM genera una disposizione casuale che potete tentare di annullare).

Veniamo quindi alla soluzione dei problemi proposti.

La tabella del Problema 1 NON e' annullabile perche' il primo invariante e' diverso da 0 modulo 3:

Invariante_1=(1+2+1+2)-(1+1+1+1)-(1+1+1+1)+(1+2+1+2)=4=1 modulo 3

La tabella del Problema 2 e' annullabile perche' gli invarianti sono tutti nulli:

Invariante_1=(1+1+1+2)-(1+1+2+2)-(1+2+1+2)+(1+1+1+1)=3=0 modulo 3
Invariante_2=(1-1)+(-1+2)+(1-2)+(1-1)+(-2+2)+(1-1)=0 modulo 3
Invariante_3=(1-1)+(1-1)+(-1+2)+(-2+2)+(1-2)+(1-1)=0 modulo 3

Si dimostra che ci sono 3^3=27 soluzioni diverse. Di queste 27, quelle con il minimo numero di click sono 6 e il minimo e' uguale a 20. Per vedere tutte le soluzioni potete utilizzare il programma scritto da ALESSANDRO LOFFREDO che trovate QUI.
Ecco le soluzioni minime possibili con a fianco i nomi di quelli che l'hanno inviata. Le caselle VERDI vanno cliccate UNA volta mentre quelle ROSSE vanno cliccate DUE volte.

I problemi proposti sono una variante modulo 3 del gioco LIGHTS OUT dove invece i numeri nelle caselle vengono invece ridotti modulo 2. La annullabilita' di una tabella binaria (LIGHTS OUT significa appunto "spegnere tutte le luci") si puo' interpretare come la risoluzione di un sistema lineare di ben 25 equazioni (le 25 caselle) in 25 incognite (le combinazioni di click) modulo 2. Nel caso modulo 3 il metodo si adatta facilmente sostituendo il campo algebrico Z_2 con Z_3. Tale metodo e' diverso dalla spiegazione che ho dato sopra che e' piu' elementare anche se meno generale. Infatti, per esempio, con l'algebra lineare si puo' spiegare perche' nel nostro caso le soluzioni, se ci sono, sono 27. La ragione e' che la matrice del sistema ha rango 22 (rispetto a Z_3) mentre lo spazio delle variabili ha dimensione 25 quindi rimangono 3 parametri liberi ciascuno da scegliere in Z_3 che ha 3 elementi quindi 3^3=27 soluzioni. Una descrizione di questo approccio con l'algebra lineare si puo' trovare su Jaap's Puzzle Page (precisamente qui). Per i piu' curiosi consiglio di provare a dare un'occhiata ai seguenti articoli: The Solving of Lights Out e Lights Out!: A Survey of Parity Domination in Grid Graphs. Ulteriori referenze si possono trovare sul sito MathWorld della Wolfram.