Consideriamo ora un nuovo sistema di coordinate cartesiano (O',i',j',k'), lo stesso punto P avrà nel nuovo sistema le coordinate (x',y',z'). In nostro scopo è quello di trovare come cambiamo le coordinate cambiando il sistema di riferimento.
Nel caso più semplice, quando cioé modifichiamo solo a posizione dell'origine, abbiamo

e quindi, se O'=(o₁,o₂,o₃) sono le coordinate della nuova origine O' nel vecchio sistema di riferimento, le relazione precedente diventa

e da questo, ordinando i fattori, abbiamo le formule cercate dirette e inverse.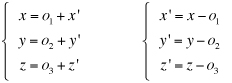

Supponiamo ora di modificare la base ortonormale senza modificare la posizione dell'origine. Scriviamo i vettori della nuova base come combinazioni lineari di quelli della vecchia base: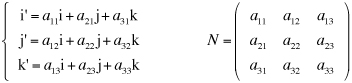

La matrice N definita come sopra si chiama matrice del cambiamento di base. Attenzione agli indici: le componenti dei vettori sono messi come colonne nella matrice N. Notiamo che il prodotto scalare i'.i' è il prodotto dalla prima colonna per la prima colonna della matrice N e, poichè i' è un versore, questo prodotto fa 1. Analogamente il prodotto scalare di i' per j' è il prodotto della prima colonna per la seconda colonna della matrice N. In generale il prodotto (righe per colonne) della matrice N^t, che ha per righe le colonne di N, con la matrice N viene la matrice identità.

Tali matrici, quelle cioè per le quali l'inversa coincide con la trasposta, si chiamano matrici ortogonali. Poiché

tali martici possono avere determinate 1 o -1. Le matrici ortogonali di determinate 1 si chiamano matrici ortogonali speciali.
Sia ora P un generico punto dello spazio e siano (x,y,z) le sue coordinate nel vecchio sistema di riferimento (O,i,j,k) e (x',y',z') quelle nel nuovo sistema (O,i',j',k'). Abbiamo dunque

e quindi, dato che un vettore si scrive in modo unico come combinazione lineare dei vettori della base, abbiamo le formule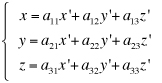

formule che, usando la notazione matriciale, possono scriversi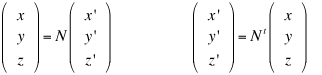

Se infine passiamo dal riferimento (O,i,j,k) al riferimento (O',i,j,k) e da questo al riferimento (O',i',j',k') le coordinate (x,y,z) si trasformeranno, cambiando origine senza cambiare base, nelle coordinate (x',y',z') e queste, cambiando base senza cambiare origine, nelle coordinate (x'',y'',z'') secondo le formule che abbiamo visto sopra: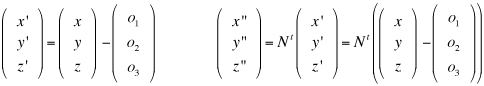

In definitiva se abbiamo due sistemi di riferimento cartesiani (O,i,j,k) e (O',i',j',k') e se, (x,y,z) sono le coordinate di un punto P nel primo sistema di riferimento e (x',y',z') quelle dello stesso punto P nel secondo sistema di riferimento, allora sussistono le relazioni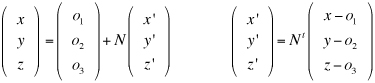

dove (o₁,o₂,o₃) sono le coordinate della nuova origine nel vecchio sistema di riferimento e N è la matrice del cambiamento di base.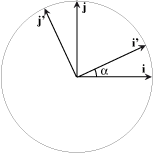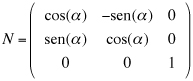

I cambiamenti di base più semplici sono quelli nei quali un vettore non cambia. Se ad esempio k=k' allora i nuovi vettori i' e j' devono essere due versori entrambi ortogonali a k e ortogonali tra loro. Quindi abbiamo i'= (i'.i)i+(i'.j)j e j'= (j'.i)i+(j'.j)j e se indichiamo con alfa è l'angolo tra i e i', la matrice del cambiamento di base sarà

             

Vediamo ora, con un esempio significativo, come sia possibile modificare il sistema di riferimento in modo che una equazione di secondo grado nelle tre incognite x,y,z, si trasformi nella equazione canonica di una quadrica nelle nuove incognite x',y',z'. Sia

essendo k una costante reale assegnata. Cominciamo col prendere in esame la forma quadratica 5x² + 4xy + 6y² - 4yz + 7z² e scriviamo la matrice simmetrica A associata a questa forma: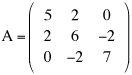

Poichè A é simmetrica un fondamentale teorema di algebra lineare ci assicura che A può essere diagonalizzata con una matrice ortogonale speciale. Per fare questo cominciamo a calcolare gli autovalori di A. Questi sono quei numeri 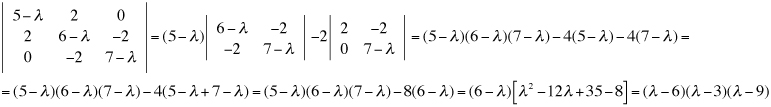per i quali il sistema (A-I)X=0 ammette soluzioni non banali. Affinché ciò avvenga è necessario che la matrice (A-I) non abbia rango massimo e quindi che det(A-I)=0. Calcolando il determinate troviamo

e quindi gli autovalori sono 3,6,9. Calcoliamo ora gli autovettori. Per fare questo dobbiamo trovare soluzioni non nulle per i tre sistemi relativi all'autovalore 3,6, 9 rispettivamente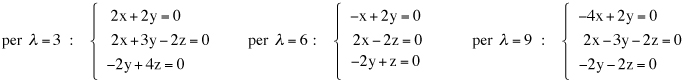

Per 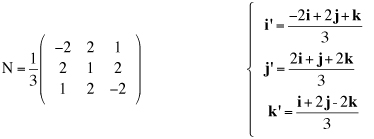=3 troviamo l'autovettore (-2t,2t,t) che normalizzato diventa (-2/3,2/3,1/3). Analogamente per =6 troviamo l'autovettore (2/3,1/3,2/3) e infine per =9 l'autovettore (1/3,2/3,-2/3). La matrice del cambiamento di base è quindi la matrice N che ha per colonne queste componenti e la nuova base è data dai vettori i', j', k':

Le formula per il cambiamento di coordinate, dirette e inverse, sono dunque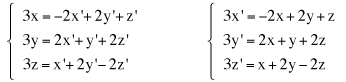

che sostituite nell'equazione iniziale forniscono la nuova equazione

Dobbiamo ora spostare l'origine completando i quadrati. Abbiamo

cioè

e, in definitiva le formule del cambiamento di coordinate sono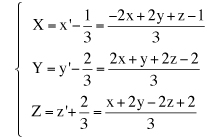

Si riconosce ora che la superficie, se k+7>0, è un ellissoide.

Esercizio
Fissato nello spazio euclideo un sistema di rferimento cartesiano (O, i,j,k), si consideri la retta che passa per il punto A=(0,0,1) e per il punto B=(a,b,0). Determinare un nuovo sistema di coordinate cartesiane nel quale il punto B sia l'origine del nuovo sistema e la retta si trovi sul piano x'=0.
Soluzione