Matematica discreta 2

Complementi ed esercizi dell'Unità 8.



Calcolo di una base per l'immagine e il nucleo di una matrice.

Le considerazioni precedenti relative allo studio generale della struttura di una trasformazione lineare hanno importanti conseguenze nello studio delle matrici. Possiamo infatti interpretare una qualunque matrice A con m righe e n colonne come una trasformazione lineare dello spazio dei vettori numerici Rn (che scriviamo come vettori colonna) nello spazio dei vettori numerici Rm (che scriviamo pure come vettori colonna). Tale trasformazione è stata denotata col simbolo LA e trasforma il vettore colonna x a n componenti nel vettore colonna y a m componenti ottenuto moltiplicando A per x:

y = LA(x) = A.x

Abbiamo visto che l'immagine di questa applicazione lineare ( detta anche immagine di A) è il sottospazio di Rm generato dalle colonne c1 , c2 , ... , cn di A:

Im LA(x) = Span(c1 , c2 , ... , cn)

mentre il nucleo (detto anche nucleo di A) è dato da tutti i vettori x di Rn tali che LA(x) = 0, cioè

Ker LA = { x ÎRn : A.x = 0}

Il problema dunque di trovare una base per il nucleo di LA è ricondotto al problema, che abbiamo già risolto, di trovare le soluzioni di un sistema lineare omogeneo in m equazioni e n incognite: il sistema appunto A.x = 0. L'algoritmo per fare questo consiste nei seguenti passi

  • si fanno operazioni elementari sulla matrice A fino a trovare una matrice B ridotta a scala con i suoi r pivot
  • si individuano le n-r variabili libere che sono quelle relative alle colonne della matrice B che non contengono i pivot
  • si attribuisce un valore arbitrario t1, t2, ... , tn-r alle variabili libere e si risolve dal basso il sistema ridotto B.x = 0
  • si individuano gli n-r vettori colonna a n componenti x1, x2, ... , xn-rche, moltiplicati per t1, t2, ... , tn-r forniscono la soluzione generica del sistema

    x = t1x1 + t1x1 + ... + tn-rxn-r

Gli n-r vettori così trovati danno una base del nucleo di A

Ker LA(x) = Span(x1 , x2 , ... , xn-r)

In particolare abbiamo che dim Ker LA = n-r essendo r il rango della matrice A, cioè il massimo numero di righe di A linearmente indipendenti. Dato che dim Im LA = dim Rn - dim Ker LA = n - (n-r) = r, aibbiamo che il rango r della matrice A da anche la dimensione dell'immagine di LA che, come abbiamo visto, è lo spazio generato dalle colonne di A. Abbiamo allora, come corollario al teorema di struttura sulle trasformazioni lineari, che

Corollario
Il massimo numero di righe indipendenti di una matrice A è uguale al massimo numero di colonne indipendenti di A.

Questo corollario ci dice anche come dobbiamo procedere per calcolare una base per Im LA.

  • si fanno operazioni elementari sulla matrice A fino a trovare una matrice B ridotta a scala con i suoi r pivot
  • le r colonne della matrice A corrispondenti alle colonne di B che contengono i pivot sono linearmente indipendenti
  • queste colonne di A, dato che sono nel numero giusto e sono indipendenti, formano quindi una base per Im LA

    Im LA = Span(ci1, ci2, ... , cir)

    dove i1, i2, ... , ir sono le r colonne di A corrispondenti alle colonne di B che contengono i pivot.

Esempio
Consideriamo la matrice

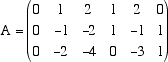essa definisce una trasformazione lineare di R6 in R3: il vettore (colonna) x = (x1, x2,x3,x4,x5,x6) si trasforma nel vettore (colonna) (y1,y2,y3) nel modo seguente: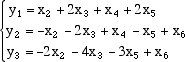

Riducendo la matrice A otteniamo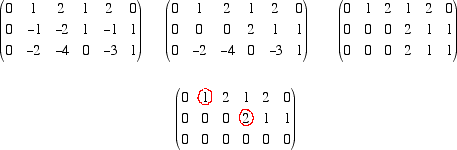

Il rango della matrice A è 2 perché la matrice ridotta B ha solo 2 righe indipendenti, quindi abbiamo dim Im LA = 2 e dim Ker LA = 6 - 2 = 4.
Una base di Im LA è data dalla sconda e quarta colonna di A (quelle che corrispondono a pivot). Se poniamo w1 = (1,-1,-2) e w2 = (1,1,0) sarà

Im LA = Span(w1,w2)

Per trovare il nucleo dobbiamo risolvere il sistema lineare omogeneo Ax = 0 equivalente al sistema ridotto Bx = 0. Prendiamo come variabili libere la prima, la terza, la quinta e la sesta (quelle che non corrispondono ai pivot). Risolvendo il sistema dal basso e ponendo x6 = t1, x5 = t2, x3 = t3, x1 = t4 abbiamo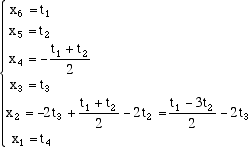

ordinando le variabili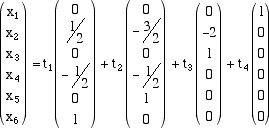

I 4 vettori colonna che abbiamo trovato in questo modo sono una base per il Ker LA.



Esercizi