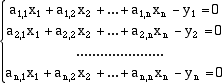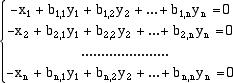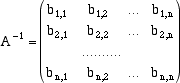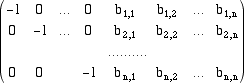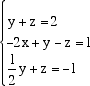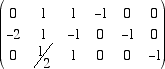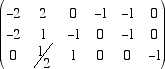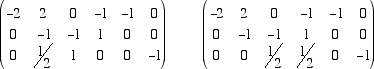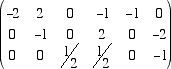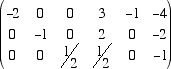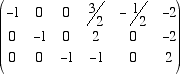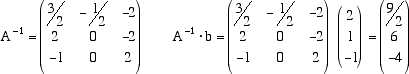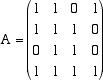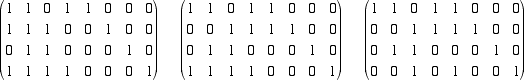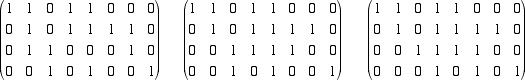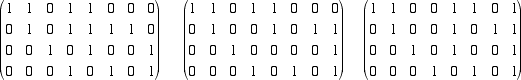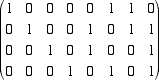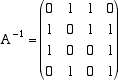Matematica discreta 2

Complementi ed esercizi dell'Unità 8.



Algoritmo di Gauss per il calcolo della matrice inversa

Diamo in questo paragrafo un algoritmo che si basa sul metodo di riduzione di Gauss con il quale calcolare la matrice inversa di una matrice quadrata A di rango massimo. Supponiamo che i numeri ai,j siano i coefficienti della matrice. Per ogni vettore (colonna) x possiamo calcolare il vettore y = A.x cioè il vettore y dato da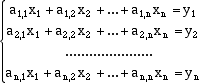

e il problema consiste, viceversa, dato il vettore y di calcolare il corrispondente vettore x, cioè dei numeri x1, x2, ... ,xn funzioni delle y, che verifichino le equazioni precedenti. L'idea dell'algoritmo consiste nel pensare il sistema precedente come un sistema omogeneo di n equazioni nelle 2n incognite x1, x2, ... ,xn e y1, y2, ... ,yn

e nel fare operazioni elementari 1 sulle equazioni del sistema (senza però fare permutazioni) fino a ridurre il sistema alla forma

La matrice di destra così ottenuta è la matrice inversa

Il motivo per il quale non si debono fare permutazioni di equazioni dipende dal fatto che nella matrice finale è importante l'ordine delle righe: la prima rapprersenta la prima incognita, la seconda la seconda ecc. ecc.
In definitiva l'algoritmo consiste nel ridurre, senza fare permutazioni di righe, la matrice di n righe e 2n colonne

nella matrice

cosa che è sempre possibile se A ha rango massimo.

Esempio
Supponiamo di dover risolvere il seguente sistema di equazioni lineari calcolando la matrice inversa con l'algoritmo di Gauss

La matrice da ridurre è la matrice

Dato che la prima colonna ha come primo elemento 0 e dato che non possiamo permutare le righe della matrice, sostituiamo, con una operazione elementare consentita, la prima riga con un'altra riga che abbia il primo elemento non nullo. Possiamo, ad esempio, sostituire la prima riga con la sua somma con la seconda riga

Cominciamo ora a fare operazioni elementari per produrre zeri sotto i pivot delle prime tre colonne

Osserviamo che, essendo la matrice dei coefficienti di rango tre, le tre colonne sono indipendenti e quindi otteniamo sempre, a questo punto della riduzione, una matriche con tutti zeri sotto la diagonale principale. Ora, a partire dall'ultima colonna produciamo degli zeri sopra i pivot. Moltiplichiamo quindi l'ultima riga per 2 e sommiamola alla seconda

Non ci resta ora che produrre uno zero sopra il pivot -1. Moltiplichiamo la seconda riga per 2 e sommiamola alla prima

Infine, moltiplicando la prima riga per 1/2 e la terza per -2, abbiamo la matrice che cerchiamo

In definitiva

e la soluzione del sistema proposto è x=9/2, y=6, z=-4.


Codici lineari

Le considerazioni precedenti possono essere utilizzate per definire dei particolari codici utili a criptare un messaggio che si vuole mantenere segreto. In generale un determinato messaggio x viene codificato in un nuovo messaggio irriconoscibile y = L(x). Questo nuovo messaggio y viene trasmesso e può essere letto da chiunque intercetti la trasmissione. Tuttavia per riconoscerlo occorre decriptarlo e per fare questo occorre conoscere l'operatore L-1 di decodifica, operatore che, si suppone, sia noto solo al destinatario del messaggio. Il destinatario dunque riceve il segnale y, lo decodifica calcolando L-1(y) e può in questo modo leggere il messaggio originale x = L-1(y). Il modo più semplice per fare questo è supporre L lineare.
Facciamo un esempio in un caso particolarmente semplice.
Supponiamo che le "parole" che si intende criptare siano solo 15 (i primi 15 numeri) che sriviamo in forma binaria con una striga formata da 4 caratteri, rispettivamente a partire da 1 fino a 15

0001, 0010, 0011, 0100, 0101, ... , 1111

con questa notazione la stringa (x1,x2,x3,x4) corrisponde al numero decimale

x123 + x222 + x32 + x4

Possiamo dunque pensare le parole come vettori dello spazio F4 di dimensione 4.
Per codificare le nostre 15 parole possiamo scegliere una qualunque matrice 4x4 con la sola condizione che sia di rango 4 in modo da poterla invertire. Prediamo ad esempio la seguente matrice

Con questo codice, la parola 9, ad esempio, che si scrive come x = (1,0,0,1) si codifica nella stringa A.x cioè, eseguendo il prodotto, in y = (0,1,0,0). Questa è la striga che viene trasmessa e che può anche essere intercettata. Il destinatario del messaggio, conoscendo il codice, può decodificare la stringa ricevuta calcolando A-1.y.
Cominciamo intanto a calcolare, una volta per tutte, l'inversa della matrice A usando l'algoritmo di Gauss e tenendo conto che nel campo F risulta sempre 1=-1.

Per produrre degli zeri nella prima colonna abbiamo sostituito la seconda riga con la somma delle prime due e la quarta con la somma della quarta con la prima. Il secondo elemento della seconda colonna è zero. Sostituiamo allora la seconda riga con la sua somma con la terza riga e facciamo operazioni elementari per produrre degli zeri sotto i pivot.

A questo punto dobbiamo produrre degli zeri sopra il pivot della quarta colonna. Per questo sostituiamo la terza riga con la sua somma con la quarta, la seconda con la sua somma con la quarta e la prima con la sua somma con la quarta.

Resta ancora da siatemare la prima riga. Per questo sostituiamo la prima riga con la sua somma con la seconda

le ultime 4 colonne della matriche che abbiamo ottenuto sono le colonne della matrice A-1 che cercavamo

Il messaggio in codice y può essere ora decodificato moltiplicandolo per la matrice A-1. Se y = (0,1,0,0) allora, eseguendo il prodotto, abbiamo A-1.y = (1,0,0,1) e quindi la parola trasmessa era 23 + 1 = 9.

Supponiamo ora che una spia, che è in grado di intercettare i messaggi trasmessi, voglia decifrarli. La spia non conosce la matrice che codifica le parole ma sa che il codice è lineare e conosce la codifica di 4 parole indipendenti. Con queste informazione è in grado di decodificare qualunque messaggio. Supponiamo ad esempio che conosca la codifica delle parole 3, 7 , 8 , 10 cioè delle tre stringhe u1 = (0,0,1,1), u2 = (0,1,1,1), u3 = (1,0,0,0), u4 = (1,0,1,0). Queste parole, usando per codificare la matrice A che abbiamo introdotto più sopra, vengono codificate con le strighe v1 = (1,1,1,0), v2 = (0,0,0,1), v3 = (1,1,0,1), v4 = (0,1,0,0). Supponiamo dunque che la spia sappia che il codice L con cui vengono trasformate le parole è lineare e sappia anche che L(u1) = v1, L(u2) = v2, L(u3) = v3, L(u4) = v4. Con queste informazioni, sapendo che u1, u2, u3, u4 sono linearmente indipendenti è possibile determinare la matrice A che descrive la trasformazione L. Sappiamo infatti che tale matrice ha come colonne i trasformati dei vettori della base canonica di F4. Siano e1 = (1,0,0,0), e2 = (0,1,0,0), e3 = (0,0,1,0), e4 = (0,0,0,1) i vettori della base canonica (che pensiamo come vettori colonna). Abbiamo e1 = u3 e quindi

L(e1) = L(u3) = v3 = e1 + e2 + e4

e quindi la prima colonna della matrice A è (1,1,0,1). Analogamente, dato che e2 = u1 + u2, abbiamo

L(e2) = L(u1) + L(u2) = v1 + v2 = e1 + e2 + e3 + e4

la seconda colonna di A è allora (1,1,1,1). Poichè e3 = u1 + u3 + u4

L(e3) = L(u1) + L(u3) + L(u3) = v1 + v3 + v4 = e2 + e3 + e4

la terza colonna di A è (0,1,1,1). Poichè, infine, e4 = u3 + u4

L(e4) = L(u3) + L(u4) = v3 + v4 = e1 + e4

e quindi la quarta colonna di A è (1,0,0,1). Una volta calcolata la matrice A è possibile, per la spia decodificare qualunque messaggio y venga trasmesso dato che attraverso A, come abbiamo fatto precedentemente, si può calcolare A-1 e quindi x = A-1y.