Matematica discreta 2

Complementi ed esercizi dell'Unità 8.



Matrici invertibili e sistemi di equazioni lineari non omogenei

Un sistema quadrato di equazioni lineari è un sistema di n equazioni in n incognite x1, x2, ... ,xn che compaiono solo al primo grado. Un tale sistema può essere scritto per esteso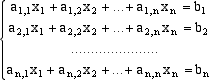

I numeri ai,j sono i coefficienti del sistema e le bi, che si trovano a secondo membro, i termini noti. Il problema consiste, dati i coefficienti e i termini noti, nel trovare, se esistono, dei numeri x1, x2, ... ,xn che verifichino contemporaneamente le n equazioni date. Utilizzando il linguaggio e l'algebra delle matrici la scrittura precedente può essere compattata nella semplicissima forma

A.x = b

dove il simbolo A rappresenta la matrice nxn i cui elementi sono i coefficienti del sistema, b la matrice (o vettore colonna) di n righe e 1 colonna formata dai termini noti e x l'analogo vettore colonna formato dalle n incognite.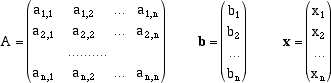

La scrittura matriciale non solo permette di compattare l'informazione, essa permette anche, per via analogica, di intuire il metodo risolutivo. Se infatti n=1 l'equazione ax = b (se a è invertibile, cioè se a è non nullo) ha come soluzione x = a-1b. La stessa situazione si ripresenta nel caso generale. Se infatti la matrice A è invertibile, allora esiste una matrice A-1 tale che A.A-1 = A-1.A = I essendo I la matrice identica. Moltiplicando a sinistra l'espressione precedente per A-1, otteniamo

A-1.(A.x) = A-1.b

ma, essendo il prodotto tra matrici associativo

A-1.(A.x) = (A-1.A).x = I.x = x

e quindi

x = A-1.b

Il problema è quindi ricondotto a quello di sapere se la matrice A è invertibile e nel caso di calcolare la sua inversa. Possiamo rispondere al primo problema se riguardiamo A come una trasformazione lineare di Rn in Rn: se infatti la trasformazione lineare LA associata ad A è biunivoca allora esiste, insiemisticamente, una trasformazione inversa la quale, essendo anch'essa lineare, è espressa da una matrice che è proprio l'inversa di A. Ma sappiamo che la trasformazione lineare LA è biunivoca se e solo se Ker LA = {0} e Im LA = Rn e questo equivale al fatto che A ha rango n. Abbiamo dunque il seguente criterio di invertibilità:

Una matrice quadrata n x n è invertibile se e solo se ha rango n.

La condizione precedente può essere verificato riducendo la matrice con l'algoritmo di Gauss o anche, come vedermo, calcolando il suo determinante.