Unità 1

Geometria ed algebra

Complementi ed esercizi dell'Unità 7.

Area di un parallelogramma.

Consideriamo lo spazio vettoriale formato dai vettori geometrici di un dato piano e siano i e j due vettori di una sua data base ortonormale. Scegliamo due ulteriori vettori vettori geometrici u e v e rappresentiamo tali vettori con due segmenti orientati con origine nello stesso punto A

u = AB = a i + b j
v = AC = c i + d j

Si forma in questo modo un parallelogramma la cui area, che non dipende dal modo con cui abbiamo rappresentato i due vettori, è nulla se e solo se i due vettori sono linearmente dipendenti. Inoltre attribuiamo a tale area il segno positivo se l'orientazione definita da u verso v (seguendo l'angolo convesso tra u e v) è concorde con quella definita dai vettori i e j, negativa in caso contrario. Indicheremo tale area con il simbolo A(u,v)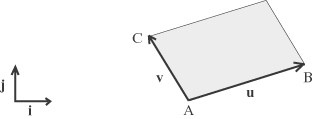

Nella figura animata possiamo muovere il punto A rappresentando diversamente i due vettori u e v e possiamo cambiare la posizione di C ottenendo aree positive e aree negative. Abbiamo ovviamente

A(u,v) = -A(v,u)

Il calcolo dell'area A(u,v) si ottiene modificando il parallelogramma senza alterarne l'area fino a ridurlo a un rettangolo i cui lati hanno una lunghezza calcolabile a partire dai dati vettori. Questa riduzione che, dal punto di vista vettoriale consiste nel sostituire una riga di una matrice con quella stessa riga più un multiplo di un'altra, da un punto di vista geometrico si ottiene in virtù della proposizione 35 del primo libro degli Elementi¹. Nella nota abbiamo trascritto la proposizione euclidea e abbiamo illustrato la sua dimostrazione con una figura animata.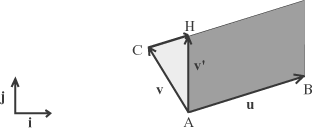
Il teorema di Euclide ci dice come "raddrizzare" il parallelogramma:

Nella figura è v' = v + CH = v + ku

Se sostituiamo il vettore v con un vettore verticale v' ottenuto aggiungendo a v un multiplo di u, l'area non cambia, ma ora, il nuovo vettore v' è un multiplo di j cioé v' = pj. Se vogliamo che il vettore v' = v + ku abbia solo la componente verticale bisognerà che

(ci + dj) + k(ai + bj) =pj

cioè k=-(c/a) e di conseguenza

Osserviamo che, se scriviamo la matrice che ha come righe le componenti dei vettori u e v e la matrice che ha come righe le componenti dei nuovi vettori u e v' abbiamo

dove la seconda matrice è ottenuta dalla prima con una operazione elementare sulle sue righe: esattamente abbiamo moltiplicato la prima riga per -(c/a) in modo da ottenere uno zero nel posto 2,1.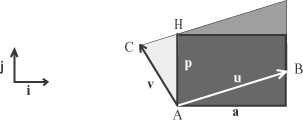
Radrizzando ulteriormente il parallelogramma aabiamo che la proiezione ortogonale di u su i cioè il prodotto scalare di u.i = a fornisce la misura della base di un rettangolo che ha la stessa area del rettangolo definito da u e v'

Abbiamo dunque

A(u,v) =A(u,pj) = ap = ad - bc

In definitiva l'area del parallelogramma definito dai vettori u e v si calcola scrivendo la matrice A che ha per righe le componenti dei due vettori, riducendo la matrice con l'algoritmo di Gauss e moltiplicando i due pivot. Tale area vale ad-bc numero che è anche chiamato il determinante della matrice e indicato con det(A) o anche con due linee verticali

Notiamo che l'interpretazione di questo numero come area ci porta a concludere che il determinante è uguale a zero se e solo se i due vettori sono dipendenti cosa che è d'altra parte evidente interpretando la relazione ad-bc = 0 come uguaglianza tra i rapporti a:c e b:d. In definitiva, data una qualunque matrice A 2x2 possiamo definire il determinante di A come lo scalare ad-cb e osservare che tale numero è nullo se e solo se le due righe della matrice, pensate come vettori numerici, sono linearmente dipendenti.

Volume di un parallelepipedo.

Consideriamo ora i vettori geometrici dello spazio tridimensionale e sia i, j, k, una base ortonormale di questo spazio. Consideriamo anche tre vettori geometrici u, v,w che rappresentiamo con tre segmenti orientati applicati allo stesso punto A

u = AB = a₁ i + a₂ j + a₃ k
v = AC = b₁ i + b₂ j + b₃ k
w = AD = c₁ i + c₂ j + c₃ k

Si forma in questo modo un parallelepipedo il cui volume, che non dipende dai segmenti con cui abbiamo rappresentato i tre vettori, è nullo se e solo se i tre vettori si schiacciano su un piano, sono cioè linearmente dipendenti.

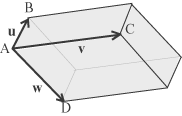
Possiamo, anche in questo caso, attribuire a tale volume il segno positivo se l'orientazione definita da u, v, w è la stessa di quella definita dai vettori i e j, k, negativa in caso contrario. Ciò significa che possiamo orientare le tre dita della mano destra (il pollice lungo la direzione e il verso di i, l'indice lungo la direzione e il verso di j e il medio lungo la direzione e il verso di k) sia secondo i, j, k che secondo u, v, w Indicheremo tale volume con il simbolo V(u,v,w). Come nel caso piano se cambiamo l'ordine di due vettori cambia il segno del volume. Ad esempio

V(u,v,w) = -V(v,u,w)
V(u,v,w) = -V(u,w,v)
ecc. ecc.

Anche in questo caso se modifichiamo il parallelepipedo sostituendo un vettore con quel vettore sommato a un multiplo di un'altro, il volume del parallelepipedo non cambia.

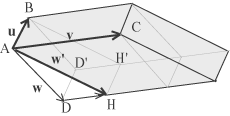Nella figura abbiamo sostituito w con w' = w + kv, dove kv = DH. Il volume del nuovo parallelepipedo è uguale a quello precedente perché questo è stato ottenuto levando al vecchio il prisma ABDD'HH' e aggiungendolo dall'altra parte al volume rimasto. Abbiamo dunque che, se sostituiamo un vettore con quel vettore sommato a un multiplo di un'altro, il volume dei due parallelepipedi non cambia.

V(u,v,w) = V(u,v,w+kv)

Questo significa che, se scriviamo la matrice che ha come righe le componenti dei vettori u, v e w e se da questa ne otteniamo un'altra eseguendo operazioni elementari sulle righe, senza fare permutazioni, il volume del parallelepipedo iniziale non cambia, mentre per ogni permutazione eseguita cambia di segno. Possiamo allora fare la riduzione di Gauss della matrice iniziale ottenendo se, come abbiamo supposto u, v e w sono linearmente indipendenti, una matrice ridotta di forma triangolare. Precisamente alla fine della riduzione avremmo i nuovi vettori

u' = p i + p'j + p'' k
v' = q j + q' k
w' = r k

V(u,v,w) = (-1)^s V(u',v',w')

essendo s il numero di permutazioni di riga eseguiti durante il processo di riduzione. Il volume del papallelepipede definito da u',v',w' si calcola facilmente infatti l'area della faccia definta dai vettori v' = q j + q' k e w'= r k, che si trovano entrambi sul piano j , k, è data, per quello che abbmo visto precedentemente, da qr, mentre l'altezza del parallelepipede rispetto a quella base è la proiezione ortogonale del vettore u' lungo la direzione di i che è quella ortogonale al piano di v' e w'. Tale proiezione ortogonale vale u' . i = p. In definitiva, se i tre vettori u,v,w sono indipendenti

V(u,v,w)= (-1)^s pqr

dove p, q, r sono i tre pivot della matrice A che ha per righe le componenti di quei vettori nella base ortonormale i, j, k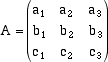

e s è il numero di permutazioni di riga eseguite durante la riduzione. Se invece i tre vettori sono dipendenti allora V(u,v,w) = 0. Notiamo che i singoli pivot non sono univocamente detrminati dalla matrice A, essi possono essere scelti con una certa libertà, tuttavia, dato che il volume del parallelepipede non dipende dal modo col quale riduciamo la matrice, il loro prodotto (a parte il segno) non cambia. Questo numero, che dipende solo dalla matrice A, si chiama il determinante di A e si indica con det(A). Precisamente, data una matrice A 3x3 , se le tre righe di A sono linearmente dipendenti allora det(A) = 0, altrimenti se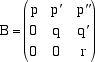

è una matrice ottenuta da A con operazioni elementari sulle righe, allora il numero (-1)^s pqr, che non dipende da come è stata ottenuta B, si chiama il determinante di A.