Matematica discreta 2

Complementi ed esercizi dell'Unità 6.



Trasformazioni lineari tra spazi vettoriali

Il modo in cui la matrici entrano prepotentemente nella matematica è la loro duttilità nel descrivere un certo tipo di trasformazioni, quelle lineari, che attraverso l'algebra delle matrici possono essere "misurate" e poi sommate e moltiplicate come fossero numeri.
A una matrice A con m righe e n colonne possiamo infatti associare una trasformazione che indichiamo col simbolo LA per evidenziare la sua stretta dipendenza da A, di Rn in Rm nel modo seguente:

In tutto questo paragrafo x sarà pensato come un vettore colonna a n componenti e il prodotto Ax va inteso come un prodotto tra la matrice A di m righe e n colonne e la matrice x di n righe e una colanna. Il prodotto risultante è una matrice di m righe e una colonna che pensiamo come un vettore colonna di Rm. Scrivendo la formula precedente componente per componente e indicando con y = LA(x) il trasformato di x, abbiamo, con ovvio significato dei simboli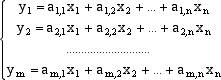

Osserviamo intanto che se B è una seconda matrice con p righe e m colonne in modo che il prodotto di matrici B.A sia definito, allora la trasformazione LB.A associata al prodotto è la composizione delle due trasformazioni: si trasforma il vettore x di Rn nel vettore y = LA(x) di Rm e questo vettore si trasforma, a sua volta, nel vettore z = LB(y) il risultato che si ottiene, essendo il prodotto di matrici associativa, è lo stesso vettore ottenuto trasformando direttamente x con LB.A. Abbiamo infatti

LB.A(x) = (B.A).x = B.(A.x) = B.LA(x) = LB(LA(x))

In formule

LB.A = LB o LA

Altre proprietà dell'algebra delle matrici si traducono, in questo contesto, in significative proprietà della trasformazione associata. Abbiamo in particolare, per ogni scelta dei vettori x e x' in Rn e per ogni scalare a in R

(1)       LA(x + x') = LA(x) + LA(x')

(2)            LA(ax) = a LA(x)             

come è facile verificare tenendo conto di come abbiamo definito LA(x).
È interessante notare come la trasformazione LA(x) agisce sui vettori della base canonica di Rn perché questo mette in relazione la trasformazione con gli elementi costitutivi della matrice. Indichiamo con e1, e2, ... ,en i vettori della base canonica di Rn : eseguendo il prodotto Ae1 , Ae2 otteniamo

cioè, in generale, l'immagine dell'i-esimo vettore ei della base canonica di Rn è la i-esima colonna ci della matrice A

LA(ei) = ci

Poichè ogni vettore x di Rn si scrive come combinazione lineare dei vettori della base canonica, usando le proprietà (1) e (2), possiamo facilmente calcolarne l'immagine. Supponiamo che sia x = x1e1 + x2e2 + ... + xnen, abbiamo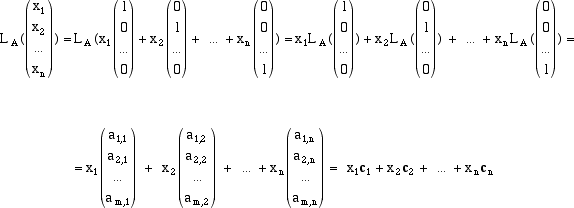

Questo calcolo mostra che l'immagine LA(x) di ogni vettore di Rn è una combinazione lineare delle colonne della matrice A. Se denotiamo con Im LA in sottospazio di Rm costituito da tutte le immagini, tramite LA, dei vettori x di Rn abbiamo la seguente importante descrizione: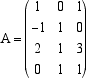

Im LA = Span(c1, c2 , ... , cn)

Esempio
Consideriamo la seguente matrice con 4 righe e 3 colonne

A definisce una trasformazione LA di R3 in R4 che trasforma il vettore colonna x di R3 nel vettore colonna y = A.x di R4; l'immagine, ad esempio, del vettore e1 - e2 + 2e3 si calcola facendo il prodotto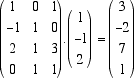

L'immagine di LA è il sottospazio di R4 generato dalle tre colonne di A. Poichè la terza colonna è la somma delle prime due, abbiamo che

dim (Im LA) = 2 e precisamente Im LA = Span(c1,c2)

In particolare LA(e1 - e2 + 2e3) = c1 - c2 + 2c3 = 3c1 + c2 è combinazione lineare delle prime due colonne di A.

Le proprietà (1) e (2) sono la base per poter definire in generale il concetto di trasformazione linare tra due spazi vettoriali arbitrari.

Definizione di trasformazione (o operatore, o applicazione) lineare tra due spazi vettoriali
Dati due spazi vettoriali V e W su un qualunque campo di scalari K (anche finito), una trasformazione lineare L di V in W è una applicazione di V in W tale che

(1)       L(x + x') = L(x) + L(x')

(2)            L(ax) = a L(x)         

per ogni scelta dei vettori x e x' in V e per ogni scalare a in K.

La nozione dunque di trasformazione lineare è legata a proprietà qualitative della trasformazione tipo il fatto che se un oggetto X si trasforma in Y allora il doppio di X si trasforma nel doppio di Y, e più in generale, un multiplo secondo a di X si trasforma nello stasso multiplo di Y. Questo permette di definire una trasformazione lineare di V in W dando l'immagine dei vettori di una base e1, e2, ... , en di V. Un generico vettore v di V si scrive infatti come combinazione lineare dei vettori della base e dunque, se L è lineare, deve essere

L(v) = L(x1e1 + x2e2 + ... + xnen) = x1L(e1) + x2L(e2) + ,..., + xnL(en)

e dunque possiamo calcolare L(v) conoscendo le componenti x1, x2, ... , xn di v e le immagini in W L(e1), L(e2), ... , L(en) dei vettori della base.

Ne caso che V sia lo spazio dei vettori geometrici di un piano, una trasformazione lineare di V in V è determinata conoscendo il valore di L sui vettori i e j di una data base di V. Nella figura animata seguente

possiamo modificare col mouse i vettori L(i) = e , L(j) = f. Fissati questi due vettori possiamo calcolare L(OP) per un generico vettore OP (che possiamo modificare agendo su P), calcolando le componenti orizzontale e verticale di OP e riportando proporzionalmente tali componenti lungo e ed f. Precisamente, se ad esempio 2 i è la componente orizzontale di OP, possiamo calcolare la sua immagine 2 L(i) = 2 e disegnado il vettore 2 e e ugualmente per la componente verticale. Nella figura animata possiamo anche vedere l'immagine di una generica circonferenza (rossa) a seconda della scelta dei vettori e ed f.

Tornando al caso in cui V = Rn e W = Rm le sole trasformazioni lineari di Rn in Rm sono quelle definite a partire da una matrice. In altri termini, se supponiamo che una trasformazione L verifichi le proprietà (1) e (2) allora, di questa trasformazione, siamo in grado di scriverne le equazioni. Precisamente sussiste il seguente teorema che caratterizza tutte le trasformazioni linari di Rn in Rm

Teorema
Se L è una trasformazione lineare di Rn in Rm allora L = LA dove A è la matrice che ha per colonne le immagini dei vettori della base canonica di Rn.
Dimostrazione
Sia e1, e2, ... , en la base canonica di Rn. Trasformiamo tali vettori con la trasformazione lineare L : otteniamo n vettori di Rm : c1 = L(e1) , c2 = L(e2) , ... , cn = L(en). Sia ora x = x1e1 + x2e2 + ... + xnen un generico vettore di Rn , possiamo calcolare, usando le proprietà (1) e (2) l'immagine L(x):

L(x) = L(x1e1 + x2e2 + ... + xnen) = L(x1e1) + L(x2e2) + ... + L(xnen) =

= x1L(e1) + x2L(e2) + .. +xnL(en) = x1c1 + x2c2 + ... + xncn

Formiamo ora la matrice A che ha come colonne i vettori c1, c2, ... , cn di Rm. Otteniamo una matrice di m righe e n colonne che definisce quindi una applicazione lineare LA di Rn in Rm. Poichè, come abbiamo visto sopra, LA(x) = x1c1 + x2c2 + ... + xncn = L(x) per ogni x di Rn abbiamo che le due trasformazioni coincidono, cioè L = LA.

Matrice associata a una trasformazione lineare

Le considerazioni precedenti possono estendersi al caso di due spazi vettoriali qualsiasi di dimensione finita. Anche in quel caso è possibile descrivere una trasformazione lineare di V in W tramite delle matrici. La differenza rispetto al caso precedente è che ora non abbiamo a disposizione una base, come la base canonica, da cui partire. In generale uno spazio vettoriale ammette infinite basi e per poter descrivere con una matrice la trasformazione lineare occorre, innanzi tutto, scegliene una e questa scelta il più delle volte non è univoca e può essere fatta in modi diversi. Per questo, in generale, parliamo di matrice associata a una data trasformazione lineare rispetto a due basi fissate, una di V e l'altra di W, cambiando le basi, cambia la matrice.
Sia dunque dim V = n , B = {v1, v2, ... , vn} una base di V, dim W = m , C = {w1, w2, ... , wm} una base di W e sia L una data applicazione lineare di V in W. A partire da questi dati possiamo costruire, come nel caso di vettori numerici, una matrice che rappresenti la trasformazione L. Tale matrice ha m righe (quanto è la dimensione di W) e n colonne (quanto è la dimensione di V), si chiama la matrice associata a L nelle basi B e C e viene indicata col simbolo M B,C(L) per evidenziare la sua dipendenza dalle basi scelte. Le colonne della matrice associata so costruiscono come nel caso precedente:

  • si prende il primo vettore v1 della base B di V
  • si trasforma il vettore v1 con la trsformazione lineare L
  • si esprime il vettore L(v1) come combinazione lineare dei vettori della base C di W

    L(v1) = a1,1w1 + a2,1w2 + ... + am,1wm

  • i coefficienti a1,1 , a2,1 , ... , am,1 , così calcolati vengono scritti nella prima colonna della matrice M B,C(L)
  • si itera il procedimento per gli altri vettori v2, ... , vn della base B costruendo nello stesso modo le altre colonne della matrice.

La matrice che abbiamo costruito descrive esattamente la trasformazione lineare L nel senso che il generico vettore v di V viene trasformato da L nel vettore w di W le cui componenti nella base C si ottengono moltiplicando per M B,C(L) le componenti di v nella base B. In altri termini se

v = x1v1 + x2v2 + ... + xnvn
allora
L(v) = y1w1 + y2w2 + ... + ymwm

dove, indicando con x e con y i vettori colonna le cui componenti sono xi (i=1,2,...,n) e yj (j=1,2,...,m),

y = A . x

dove A . x è il prodotto della matrice A = M B,C per il vettore numerico formato dalle componenti di v.

Esempio
Consideriamo lo spazio vettoriale

e sia L l'applicazione lineare di V in V che trasforma il vettore (x1,x2,x3,x4,x5) nel vettore (x3,x4,x1,x2,x5). Vogliamo innanzi tutto trovare una base B di V e poi la matrice MB,B associata a L in tale base. Si vede facilmente, risolvendo il sistema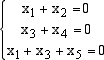


che dim V = 2 e che una sua base è formata dai vettori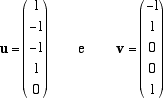


Dunque V = Span(u,v) e possiamo scegliere come base di V la base B = {u,v}. La matrice che cerchiamo è dunque una matrice 2x2 e le sue colonne si calcolano trasformando con L i vettori u e v e scrivendo il risultato come combinazione lineare di u e v. Poichè L((x1,x2, x3,x4,x5)) = (x3,x4,x1,x2,x5), abbiamo L((1,-1,-1,1,0)) = (-1,1,1,-1,0) e L((-1,1,0,0,1))= (0,0,-1,1,1) e dunque

L(u) = -u    
L(v) = u + v

e quindi la matrice associata a L nella base u e v è

Osserviamo che se w è il vettore colonna che ha come componenti (0,0,-1,1,1) anche i vettori v e w formano una base si V e, chiamando C = {v , w} questa secona base, possiamo calcolare, per esercizio, le matrici MB,C, MC,C, MC,B. Poichè

L(u) = v - w
L(v) = w      

la matrice associata MB,C è


Analogamente le matrici MC,C e MC,B sono, rispettivamente


Osserviamo che la matrice MC,B è la matrice inversa della matrice MB,C e che la matrice MC,C sembra più semplice delle altre.
In conclusione una stessa trasformazione lineare può rappresentarsi con diverse matrici a seconda di come vengono scelte le basi e si pone il problema, che sarà parzialmente risolto più avanti, di trovare il modo per scegliere intelligentemente la base di V: più la matrice che rappresenta la trasformazione è semplice più sarà facile studiare la trasformazione stessa, ad esempio valutarne asintoticamente le sue iterate.

Esercizi