Lezioni di Geometria

Franco Ghione

Coordinate cartesiane nello spazio euclideo tridimensionale

Un sistema di riferimento cartesiano nello spazio euclideo è dato quando si sia fissata una unità di misura per le lunghezze, un punto O detto origine ¹ del sistema di riferimento e una terna di vettori i, j, k a due a due ortogonali e di modulo uno. Una volta che sia stato fissato un sistema di riferimento cartesiano, è possibile associare in modo univoco, ad ogni punto P dello spazio una terna ordinata di numeri reali detti le coordinate cartesiane di P nel dato riferimento. Per determinate tali coordinate si considera il vettore geometrico OP e si scrive come combinazione lineare dei vettori i, j e k che formano una base per lo spazio dei vettori geometrici. I coefficienti di questa combinazione lineare, che sono univocamente determinate da P, sono le coordinate di P :

e si scrive P = (x,y,z).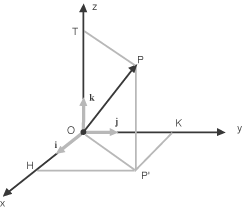
Le tre rette a due a due ortogonali che passano per O e che sono parallele ai vettori i, j e k si chiamano assi coordinati rispettivamente l'asse dell x, l'asse delle y e l'asse delle z.

Se P' è la proiezione ortogonale di P sul piano orizzontale e se H e K sono le proiezioni ortogonali di P' sugli assi x e y rispettivamente, allora

OP = OH + HP' + P'P = xi + yj + zk

e quindi le tre coordinate di P si interpretano come le lunghezze (con segno) dei segmenti

x = OH , y = OK , z = OT

Se A = (x₁,y₁,z₁) e B = (x₂,y₂,z₂) sono due generici punti dello spazio, la loro distanza è data dal modulo del vettore AB. Poiché AB =AO + OB = OB - OA e poiché, per come sono state definite le coordinate, OA = x₁i + y₁j + z₁k e OB = x₂i + y₂j + z₂k, abbiamo:

(formula 1)

Calcolando il modulo di questo vettore abbiamo la formula che da la distanza tra A e B in funzione delle loro coordinate

(formula 2)

Usando il fatto che la sfera è il luogo dei punti dello spazio che hanno distanza fissa da un dato punto detto centro della sfera, un punto generico P = (x,y,z) dello spazio appartiene alla sfera di raggio r e centro C = (x₁,y₁,z₁) se e solo se

(equazione della sfera)

Ad esempio i punti P dello spazio le cui coordinate verificano l'equazione

formano una sfera di centro C=(1,0,0) e raggio 2. Infatti completando il quadrato x²-2x troviamo

Esercizi