Soluzione

Teorema di Pitagora

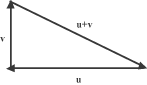
Siano u e v i vettori rappresentati dai cateti di un dato triangolo rettangolo orientati come in figura. L'ipotenusa del triangolo rettangolo rappresenta il vettore u + v e i moduli di questi vettori sono le lunghezze dei segmenti da cui derivano. Per l'ipotenusa abbiamo:

(u + v).(u + v) = u.u + 2u.v + v.v = u.u + v.v

Dal momento che i vettori u e v sono ortogonali tra loro. Abbiamo dunque

|u + v|² = |u|² + |v|²

che è l'enunciato del teorema di pitagora.


Teorema di Carnot (1753-1823)
Il teorema di Carnot estende quello di Pitagora al caso in cui il triangolo non sia necessariamente rettangolo. Esso permette di calcolare il terzo lato di un triangolo conoscendo due lati e l'angolo compreso.


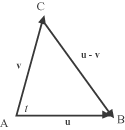
Procediamo come nel caso precedente: dobbiamo solo cambiare il verso dei vettori affichè l'angolo t interno al triangolo sia l'angolo compreso tra i due vettori u e v. Abbiamo

(u - v).(u - v) = u.u - 2u.v + v.v.
Dunque

|u - v|² = |u|² + |v|² -2|u||v|cos(t)
Cioè
BC² = AC² + AB² - 2 AC.AB cos(t)
Quando l'angolo t è retto il coseno è zero e si ritrova, come caso particolare, il teorema di Pitagora.


Teorema del triangolo inscritto in un semicerchio
Se un triangolo inscritto in una circonferenza ha un diametro come lato, allora il triangolo è rettangolo e quel lato è l'ipotenusa.


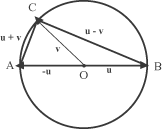
Sia O il centro della circonferenza, poniamo, come nella figura, OB = u, OC = v. Questi vettori, essendo rappresentati da raggi di una stessa circonferenza hanno lo stesso modulo, inoltre i lati AC e BC del triangolo rappresentano i vettori u + u e u - v. Per vedere se sono ortogonali basta calcolare il loro prodotto scalare:

(u + u).(u - v) = u.u - v.v = |u|² - |v|² = 0.


I teorema di Euclide
In un triangolo rettangolo il quadrato su un cateto è equivalente al rettangolo che ha per lati la proiezione ortogonale di quel cateto sull'ipotenusa e l'ipotenusa stessa.

Questo teorema non viene enunciato esplicitamente da Euclide ma viene utilizzato per dimostrare il teorema di Pitagora che risulta facilmente da questo enunciato.

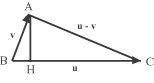
Poniamo, come nella figura, BC = u, BA = v, il secondo cateto del triangolo rettangolo rappresenterà il vettore u - v. Sapendo che il triangolo è rettangolo e interpretando il prodotto scalare di v con u in termini di proiezione ortogonale, abbiamo:

0 = v.(u - v) = v.u - v.v = BH.|u| - |v|² = BH.BC - AB²