Esercizi

Esercizio 1
Dimostrare usando i vettori geometrici e il prodotto scalare che in un rombo le diagonali sono perpendicolari.

Soluzione


Esercizio 2
Calcolare il modulo dei seguenti vettori numerici u = (1,-1,2,0), v = (3,1,1,3), w = (1,1,0,2), z = (0,-1,1,0), ed indicare, tra questi, le coppie di vettori ortogonali.

Esercizio 3
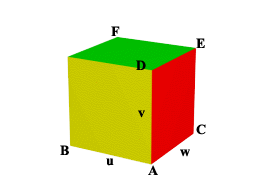
Dato un cubo con gli spigoli unitari, siano u,v,w i vettori rappresentati da tre spigoli uscenti da uno stesso vertice A. Calcolare l'angolo che la diagonale del cubo forma coi tre spigoli.

Soluzione

Esercizio 4
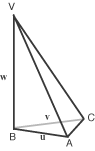
Consideriamo una piramide che ha per base un triangolo A, B, C rettangolo in B coi cateti BA e BC di lunghezza unitaria. Sia V il vertice della piramide che supponiamo si trovi sulla retta passante per B e perpendicolare al piano A, B, C. Se aumenta l'altezza BV della piramide l'angolo AVC tende a zero. Determinare da che altezza in poi quest'angolo è minire di 45 gradi.
Soluzione

Esercizio 5
Dimostrare che quattro vettori non nulli, u,v,w z a due a due ortogonali, sono lineramente indipendenti
Soluzione

Esercizio 6
Dimostrare, usando le proprietà del prodotto scalare, il teorema di Pitagora, il teorema di Carnot, il teorema del triangolo inscritto in un semicerchio (Talete), il I teorema di Euclide.
Soluzione