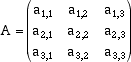
Sviluppando il calcolo, come abbiamo fatto nel caso delle coniche, troviamo

L'equazione di secondo grado in x,y,z che abbiamo trovato è l'equazione cartesiana della quadrica nel riferimento (O,i, j, k). Osserviamo che, viceversa, ogni equazione di secondo grado in x,y,z di quella forma, rappresenta una quadrica con centro in O. La matrice simmetrica, e quindi l'operatore L da cui proviene, si ottiene a partire dai coefficienti dell'equazione. L'elemento di posto i,j di questa matrice si calcola in modo che la matrice A così individuata restituisca l'equazione da cuisiamo partiti. Precisamente l'elemento di posto 1,1 è il coefficiente di x², l'emento di posto 1,2 il coefficiente di xy diviso 2, quello di posto 1,3 il coefficiente di xz diviso 2 e di seguito gli altri seguendo il seguente schema nel quale il monomio indicato indica il coefficiente da inserire nella matrice A

Potremmo ora, per avere un'idea della forma della quadrica, tentare di calcolare un certo numero di soluzioni (x,y,z) dell'equzione e rappresentare tali punti nello spazio. Questo metodo tuttavia, non è di facile realizzazione, non è molto preciso ed è poco generale. Se invece seguiamo la strada che abbiamo seguito nel caso delle coniche, le cose sono molto più facili.

Dato che l'operatore L è un operatore simmetrico sappiamo che esiste una base ortonormale di autovettori di L. Sia C = {e , f , g} tale base. Se (x',y',z') sono le coordinate di P nel nuovo riferimento, quello definito da O e da e , f , g, allora, dal momento che, essendo e , f , g una base ortonormale di autovettori

e quindi e.L (e) = e.(le) = l,   e.L (f) = e.(mf) = 0, ecc. ecc. e in definitiva, l'equazione della quadrica nelle nuove coordinate diventa

L'equazione che abbiamo trovato, non contenedo termini rettangolari è evidentemente più semplice da studiare. Possiamo, ad esempio, se n non è zero, risolvere l'equazione rispetto a z e descrivere la superficie attraverso due metà simmetriche rispetto al piano orizzontale x,y, una per valori positivi di z e l'altra per valori negativi

Questo è infatti il metodo che viene usato dai programmi di grafica digitale coi quali è possibile rappresentare in 3 dimensioni le superfici di equazione z = F(x,y) con una certa precisione. Possiamo ora procere alla classificazione di tutte le quadriche a centro a partire dagli autovalori e dagli autovettori della matrice simmetrica A. Ordiniamo nel seguito i tre autovettori e relativo a l , f relativo a m, g relativo a n denotando, per semplificare la notazione, ancora con x (anxich%egrave x'), y e z i tre assi definiti rispettivamente dagli autovettori e, f e g.

I caso (ellissoide)
Gli autovalori sono tutti positivi: 0 < l < m < n. In questo caso la quadrica si chiama ellissoide e la sua equazione canonica diventa

dove abbiamo posto a² = r²/l, b² = r²/m, c² = r²/n.
Per capire come è fatta questa superficie possiamo calcolare le curve di livello. Possiamo cioè affettare la superficie con piani paralleli al piano x,y e vedere alle varie quote z la forma della curva che si ottine. Fissata una quota z=h la curva che si ottine a quella quota ha equazione

queste curve sono non vuote solo per h <|c|. Pe h=c abbiamo un solo punto il punto (0,0,c), quando h comincia a decrescere abbiamo delle ellissi simili tra loro che diventano sempre più grandi. Per h=0 abbiamo l'ellissi maggiore. Per h<0 la sitazione si ripete simmetricamente rispetto al piano x,y.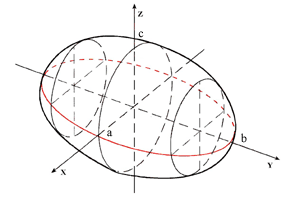

II caso (iperboloide a una falda)
Abbiamo due autovalori positivi e un autovalore negativo : 0 < l < m, n < 0. In questo caso la quadrica si chiama iperboloide a una falda e la sua equazione canonica diventa

dove, analogamente al caso precedente, abbiamo posto a² = r²/l, b² = r²/m, c² = -r²/n.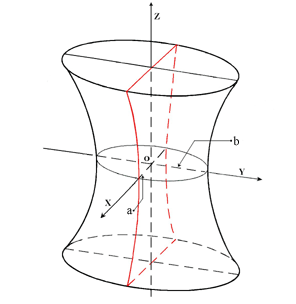
In questo caso le curve di livello sono, per ogni valore di z, delle ellissi simili tra loro che, al crescere di z, diventano sempre più grandi.

Nella figura abbiamo disegnato in rosso l'intersezione ella quadrica col piano y = 0 che è l'iperbole di equazione

Nel caso in cui i due autovalori positivi sono uguali abbiamo a=b e le ellissi sono delle circonferenze. In questo caso la superficie può essere anche generata ruotando l'iperbole rossa attorno all'asse delle z.

III caso (iperboloide a due falde)
Abbiamo un autovalore positivo e due autovalori negativi : 0 <l, m< n < 0. In questo caso la quadrica si chiama iperboloide a due falde e la sua equazione canonica diventa

dove, analogamente al caso precedente, abbiamo posto a² = r²/l, b² = -r²/m, c² = -r²/n.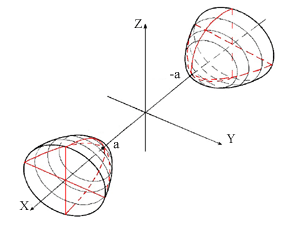
In questo caso conviene "affettare" con piani paralleli al piano che contiene gli assi y,z. Solo per |x| > |a| otteniamo dei punti e, quando questo, le sezioni sono ellissi simili tra loro.

Anche ora, se i due autovalori negativi m e n sono uguali allora le ellissi sono delle circonferenze e l'iperboloide è ottenuto ruotando attorno all'asse x l'iperbole del piano degli assi x ,z (disegnata in rosso nella figura) di equazione

IV caso (ellissoide a punti immaginari)
I tre autovalori sono tutti negativi. In questo caso l'equazione

non ha nessuna soluzione reale e la superficie da essa definita è priva di punti.


V caso (quadriche semplicemente degeneri)
Supponiamo che un autovalore sia nullo: n = 0. In questo caso l'equazione della quadrica diventa

e questa equazione rappresenta un cilindro conico con l'asse parallelo all'asse delle z. Infatti se un punto P₀ = (x₀,y₀,0) del piano x,y appartine alla quadrica (cioè verifica la sua equazione) anche tutti i punti P = (x₀,x₀,t) della retta per P₀ parallela all'asse delle z, appartengono alla quadrica, dal momento che, non comparendo z nella sua equazione, ne verificano l'equzione per ogni valore di t.
La forma della quadrica è dunque quella di un cilindro la cui base è la conica del piano x,y di equazione lx²+my²=r² le cui direttrici sono rette parallele all'asse z. Abbiamo allora 3 tipi di cilindri:

• il cilindro ellittico se l > m > 0

• il cilindro iperbolico se l > 0 e m < 0

• il cilindro a punti immaginari se l < m < 0

VI caso (quadriche doppiamente degeneri)
Se due autovalori sono nulli: m = n = 0. l'equazione della quadrica diventa

che rappresenta una coppia di piani paralleli se l > 0, mentre, in caso contrario, la quadrica è priva di punti reali.

In definitiva il calcolo degli autovalori mi dice la forma della quadrica mentre il calcolo degli autovettori mi dice la disposizione dei tre assi di simmetria.

Esempio
Considerimo la quadrica che, nel riferimento cartesiano (O,i,j,k) ha equazione

Dato che, nella matrice che definisce la quadrica, i coefficienti dei termini misti vanno divisi per 2, per non avere frazioni, conviene moltiplicare per 2 l'intera equazione e considerare la forma equivalente 2xz - 2xy + 2yz = 4. La matrice simmetrica che definisce questa quadrica è ora la matrice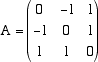

Per determinare di che tipo di quadrica si tratti basta calcolare gli autovalori della matrice simmetrica A. Il suo polinomio caratteristico è il polinomio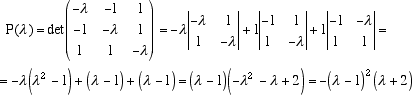

Abbiamo dunque un autovalore negativo n = -2 e due autovalori positivi uguali l = m = 1. Possiamo dunque concludere che la quadrica è un iperboloide di rotazione a una falda. Per trovare la sua disposizione nello spazio possiamo calcolare gli autovalori. L'autovalore relativo all'autovalore -2 dà la direzione dell'asse attorno a cui ruota l'iperbole, asse che chiamiamo Z ( quello relativo al terzo autovalore) mentre gli autovettori relativi all'autovalore 1 definiscono un piano (il piano X,Y) ortogonale all'asse delle Z. Calcoliamo intanto il terzo autovettore g. Dobbiamo risolvere il sistema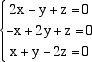

un matrice ridotta del sistema è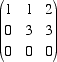

e quindi un autovettore relativo all'autovalore -2 è i + j - k Normalizzando questo autovettore otteniamo l'autovettore g

Dato che sappiamo, dalla teoria generale, che la matrice A è diagonalizzabile e che esiste una base ortonormale di autovettori, possiamo concludere che esistono altri due autovettori indipendenti (quelli relativi all'autovalore doppio l = 1) e che questi definiscono un piano ortogonale a g. Scegliamo allora su questo piano due vettori indipendenti e ed f di modulo 1 e ortogonali tra loro (che non ci interessa calcolare esplicitamente). Nel nuovo sistema di riferimento (0,e,f,g) l'equazione della quadrica diventa

e la sua forma è descritta dalla figura seguente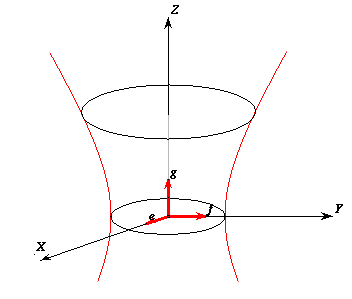

Sul piano X,Y abbiamo una circonferenza di raggio 2 mentre sul piano Y,Z l'iperbole Y² - 2Z² = 4. E' chiaro che la posizione iniziale degli assi x,y,z è inessenziale per derminare la forma della quadrica.

Esercizi