Unità 11

Matematica discreta 2

Complementi ed esercizi dell'Unità 11.

Coniche a centro e loro forma canonica.

Fissiamo un piano P e consideriamo lo spazio vettoriale V formato dai suoi vettori geometrici. Tale spazio ha dimensione 2 ed è dotato di un prodotto scalare. Ricordiamo che un sistema di riferimento cartesiano per il piano P è dato da un punto O del piano, detto origine del sistema di riferimento, e da una base ortonormale B = {i , j} di V. Le coordinate (x,y) di un punto P del piano, nel dato riferimento, sono, per definizione, le componenti del vettore OP nella base B :

OP = x i + y j

Se prendiamo un'altra base C = {e , f} lo stesso punto P viene rappresentato da due diverse coordinate (x',y'). Il legame tra le vecchie e le nuove coordinate dipende dal legame tra le due basi che abbiamo scelto. Consideriamo la matrice del cambiamento di base U = M_C,B che esprime i vettori della nuova base C come combinazioni lineari dei vettori della vecchia base B:

La matrice U è quella che ha per colonne le componenti dei vettori e e f nella base i e j

Notiamo che la matrice U è ortogonale dato che i vettori e ed f sono una base ortonormale. Ciò significa che la sua inversa, che esprime i vettori i e j come combinazioni lineari di e e f, coincide con la trasposta

U . U^t = U^t . U = Id ovvero U^-1 = U^t

Possiamo ora calcolare la relazione che tale cambiamento di base induce sulle coordinate del punto P

OP = x'e + y'f = x' (p_1,1 i + p_2,1 j) + y' (p_1,2i + p_2,2j) =
(x' p_1,1 + y' p_1,2) i + (x' p_2,1 + y' p_2,2) j = x i + y j

quindi

formula che possiamo scrivere in modo più compatto usando i prodotti tra matrice. Indicando con x il vettore colonna che ha per componenti le coordinate (x,y) e con x' quello relativo a (x',y') abbiamo

x = U x' o, inversamente x' = U^-1 x

Notiamo questa inattesa inversione: le formule che esprimono le nuove oordinate (x',y') in funzione delle vecchie (x,y) si ottendono con la matrice U^-1 che esprime i vettori della vecchia base B come combinazioni lineari di quelli della nuova base C.

Le considerazioni che abbiamo fatto possono facilmente estendersi allo spazio a tre dimesioni. Lo spazio dei vettori V ha ora dimensione tre; un sistema di riferimeto cartesiano nello spazio, come abbiamo visto, è definoto da un punto O e da una base B di V ortonormale. Se consideriamo un'altra base ortonormale C per esprimere le coordinate di un punto e se U è la matrice 3x3 del cambiamento di base, che esprime i vettori della base C come combinazioni lineari di quelli della base B, allora le stesse formule (interpretando ovviamente x e x' come vettori a tre componenti) esprimono la relazione tra le vecchie e le nuove coordinate di uno stesso punto P dello spazio.

Consideriamo ora un piano P, un suo punto O e lo spazio vettoriale V dei suoi vettori geometrici.

Definizione (di conica a centro)
Dato un operatore simmetrico L di V in V e un numero reale r non nullo, una conica di centro O è il luogo dei punti P del piano tali che il prodotto scalare di OP con L(OP) si mantiene costante

OP.L(OP) = r²

Per definire una conica occorre quindi partire da un operatore simmetrico L. Il caso più semplice è quando L è l'identità: in questo caso L(OP) = OP e la conica diventa il luogo dei punti del piano tali che

OP.OP = |OP|² = r²

cioè una circonferenza di centro O e raggio r.
Notiamo che, in generale una conica a centro è simmetrica rispetto al suo centro. Se infatti P è un punto della conica cioè se OP.L(OP) = r² anche il punto Q simmetrico di P rispetto ad O appartiene alla conica dato che OQ = -OP e

-OP.L(-OP) = OP.L(OP) = r².

Per capire la forma geometrica di una conica a centro conviene introdurre un sistema di coordinate cartesiano e vedere quale relazione algebrica debbono soddisfare le coordinate di un punto P che appartiene a una conica a centro. Fissiamo dunque una base ortonormale B = {i , j} e sia A la matrice associata a L in questa base:

L(i) = a_1,1i + a_2,1j
L(j) = a_1,2i + a_2,2j

dato che L è un operatore simmetrico e B è una base ortonormale, a_1,2 = i.L(j) = L(i) .j = a_2,1, la matrice A è simmetrica. Sia P = (x,y) un generico punto del piano, il punto P appartiene alla conica se e solo se OP.L(OP) = r², cioè se e solo se

(x i + y j).L(x i + y j) = (x i + y j) .[x (a_1,1i + a_2,1j) + y (a_1,2i + a_2,2j] =
= a_1,1 x² + 2 a_1,2 x y + a_2,2 y² = r²

L'equazione di secondo grado in x,y che abbiamo trovato è l'equazione cartesiana della data conica nel riferimento (O,i, j). Potremmo ora, per avere un'idea della forma della conica, tentare di calcolare un certo numero di soluzioni (x,y) dell'equzione e disegnare tali punti sul piano cartesiano. Questo metodo non è molto preciso e è poco generale: per ogni equazione si deve descrivere per punti le soluzioni ogni volta in modo diverso a seconda dei coefficenti dell'equazione. Un'idea diversa e molto importante consiste invece nel tentare di descrivere la conica in un sistema di riferimeto opportuno in modo che, in quel riferimeto, l'equazione sia particolarmente semplice da studiare.
Dato che l'operatore L è un operatore simmetrico sappiamo che esiste una base ortonormale di autovettori di L. Sia C = {e , f} tale base. Se (x',y') sono le coordinate di P nella nuova base, allora P appartiene alla conica definta da L se e solo se

(x' e + y' f).L(x' e + y' f) = (x' e + y' f).(x' L(e) + y' L(f)) =
= (x' e + y' f).(x' le + y' mf) =

= l(x')² + m(y')² = r²

dal momento che, essendo e ed f gli autovettori di L

L(e) = le
L(f) = mf

L'equazione che abbiamo trovato, non contenedo il termine rettangolare in xy è evidentemente più semplice da studiare. La forma della conica dipende solo da segno degli autovalori. Abbiamo infatti poche possibilità.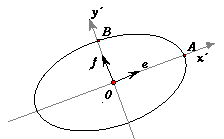

I caso (ellisse)
Gli autovalori sono entrambi positivi: 0 < l < m. In questo caso la conica è una ellisse.

Ponendo a² = r²/l e con b² = r²/m l'equazione della conica (detta canonica) diventa

Intersecando con l'asse delle ascisse y'=0 ricaviamo le coordinate del punto A, nel sistema di riferimento (O,e,f): esse sono (a,0). Analogamente ponendo x'=0 troviamo le coordinate del punto B =(0,b).
L'equazione canonica di una ellisse ci suggerisce un modo semplice per esprimere le coordinate di un suo punto in funzione di un parametro t. Se infatti t è un angolo variabile da 0 a 2p, pioché cos² + sen² = 1 le equazioni (dette equazioni parametriche)

rappresentano, per ogni valore di t, un punto dell'ellisse. Questo ci permette di disegnare facilmente una ellisse: basterà disegnare due circonferenze concentriche, una di raggio a e una di raggio b e, per ogni valore dell'angolo t, disegnare il punto (a.cos(t),b.sen(t))

Nella precedente figura animata l'angolo t è l'angolo giallo TOA che può essere modificato agendo col mouse sul punto T, il cerchio rosso ha raggio a e può essere modificando spostando il punto 2, mentre il cerchio nero ha raggio b che può pure essere modificato agendo sul punto 1. Dalla figura si vede chiaramente che OA = a.cos(t), AP = b.sen(t) e quindi il punto P è un punto dell' ellisse per ogni scelta di t.

II caso (iperbole)
Gli autovalori sono di segno alterno : m < 0 < l. In questo caso la conica è una iperbole.

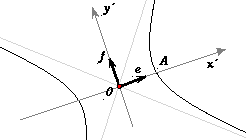Ponendo a² = r²/l e con b² = -r²/m l'equazione della conica (detta canonica) diventa

Ponendo y'=0 troviamo le coordinate del punto A, nel sistema di riferimento (O,e,f): esse sono (a,0). L'asse delle ordinate invece non interseca la curva.

III caso (ellisse a punti immaginari)
Gli autovalori sono entrambi negativi. In questo caso l'equazione

l(x')² + m(y')² = r²

non ha nessuna soluzione reale e la curva da essa definita è priva di punti.
Anche il caso in cui un autovalore è zero e l'altro è negativo è analogo a questo e la conica che ne deriva è priva di punti.

IV caso (due rette parallele) Un autovalore è nullo e l'altro è positivo. In questo caso la conica si dice degenere, la sua equazione diventa

e la sua forma è data dall'unione delle due rette verticali le cui equazioni sono scritte in parentesi.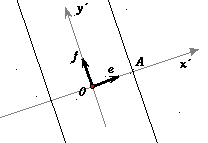

Esempio
In un piano P considerimo la conica che, nel riferimento ortonormale (O,i,j) ha equazione

10 x² + 4 xy + 7 y² = 4

Tale conica è definita dalla matrice

Per determinare di che tipo di conica si tratti basta calcolare gli autovalori della matrice simmetrica A (attenzione al fatto che l'elemeto a_1,2 della matrice A si ottiene dividendo per 2 il coefficiente di xy). Il polinomio caratteristico della matrice A è il polinomio

P(l) = l² - 17l + 66

le sue radici sono l = 11 e l = 6. Possiamo dunque concludere che la conica è una ellisse i cui semiassi valgono

Per trovare il cambiamento di riferimento che porta l'ellisse nella sua forma canonica, dobbiamo calcolare gli autovettori della matrice A. Per l = 11 abbiamo l'autovettore 2i + j , mentre per l = 6, l'autovettore -i + 2j. Dividendo questi vettori per il loro modulo otteniamo la base ortonormale di V formata da autovettori: essa è la base C = {e , f} dove

La matrice U del cambiamento di base è la matrice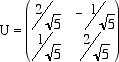

e le formule che esprimono le nuove coordinate in funzione delle vecchie, che si ottengono con la matrice trasposta, sono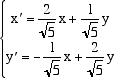

La seguente figura illustra la situazione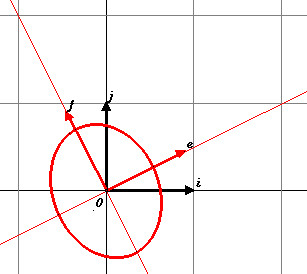

i nuovi assi, disegnati in rosso, passano per i punti di coordinate (nel vecchio sistema di riferimento) (2,1) e (-1,2) che sono le componenti dei due autovettori prima che li normalizzassimo.

Esercizi