La condizione precedente garantisce infatti che il sistema

ammetta qualche soluzione x non nulla. Il calcolo di questo determinate per matrici grandi diventa molto dispendioso dal punto di vista algoritmico richiedendo in generale n! operazioni.
In più, una volta che si sia calcolato il polinomio caratteristico resta il problema di determinare la sue radici che sono appunto gli autovalori della matrice A. Tali radici, essendo in generale espresse da numeri irrazionali, possono essere esplicitamente calcolate solo attraverso un procedimento di aprossimazione.
Da un punto di vista algoritmico vi sono dunque due difficoltà per il calcolo degli autovalori

• il calcolo del polinomio caratteristico
• il calcolo delle soluzioni di una equazione algebrica

Per aggirare queste difficoltà si sono cercati diversi metodi per il calcolo degli autovalori, i quali, come vedremo possono, viceversa, essere anche usati per risolvere, per approssimazioni successive, le equazioni algebriche.
Uno di questi metodi si basa sul calcolo delle iterate di una matrice. Esso è molto semplice, ma ha il difetto di fornire un algoritmo effettivo solo se applicato a matrici diagonalizzabili cosa che spesso è difficile da sapere a priori, senza cioè aver visto come sono gli autovalori e gli autospazi. Esistono tuttavia alcune grandi classi di matrici, ad esempio le matrici simmetriche, per le quali sappiamo, in virtù di un importante teorema, che sono sempre diagonalizzabili.
Sia dunque A una matrice diagonalizzabile, siano l₁, l₂, ... , l_n i suoi autovalori, non necessariamente distinti, e sia P la matrice le cui colonne sono gli autovettori di A. Abbiamo

essendo L la matrice diagonale che ha gli autovalori sulla diagonale principale. Se eseguiamo le potenze successive di A otteniamo, essendo il prodotto di matrici associativo

Dato che sappiamo calcolare le potenze della matrice L facendo le potenze degli elementi sulla diagonale, possiamo, con ovvio significato dei simboli, esplicitare il prodotto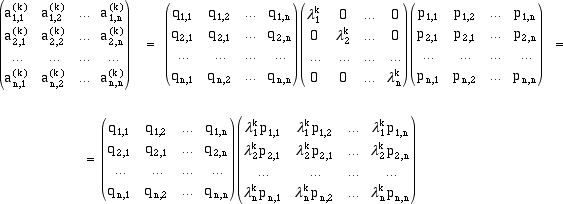

eseguendo anche l'ultimo prodotto indicato troviamo che l'elemento si posto i,j della matrice A^k, cioè il prodotto della i-esima riga della matrice P^-1 = ((q_i,j)) per la j-esima colonna della matrice a sinistra L^kP, è dato da

Supponiamo ora che autovalori distinti abbiano moduli dististinti, che l₁ sia l'autovalore di modulo massimo (eventualmente ripetuto)

e che gli elementi di posto i,j (ad esempio 1,1) di tutte le matrici A^k siano non nulli in modo che si possa formare il rapporto

dividendo, a secondo membro numeratore e denominatore per l'autovalore di modulo massimo elevato a k e facendo il limite per k tendente all'infinito, otteniamo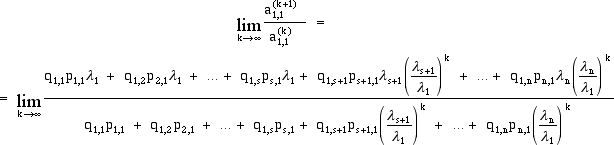

Dato che, per h=s+1,s+2, ... , n, abbiamo

e, in definitiva

Se dunque la matrice A è diagonalizzabile ed esiste un solo autovalore (eventualmente ripetuto s volte) di modulo massimo, questo autovalore si approssima col rapporto tra due elementi, il primo della matrice A^k+1 e il secondo nella matrice A^k, che abbiano la stessa posizione. Maggiore è k, migliore è l'approssimazione dell'autovalore.

Esempio
Consideriamo la matrice

calcolando le sue prime 8 potenze otteniamo le matrici

calcoliamo ora i rapporti tra gli elemeti di posto 1,1 in due matrici successive: abbiamo

Notiamo che già dopo A⁴ la prima cifra decimale si stabilizza al valore 4, dopo A⁵ anche la seconda cifra decimale si stabilizza sul valore 1, per ottenere la terza cifra decimale dobbiamo arrivare ad A⁶. In definitiva dopo sole 8 potenze abbiamo il valore dell'autovalore con 3 cifre decimali chiaramente stabili.
Seguendo il metodo tradizionale, che in questo caso non presenta certo difficoltà, occorre prima di tutto calcolare il polinomio caratteristico.

le cui radici sono e . Il valore che abbiamo trovato 2,4142 approssima l'autovalore . In questo modo abbiamo ottenuto, come stima per la radice quadrata di 2, il valore 1,4142 che fornisce esattamente le prime 4 cifre decimali di questo numero.

Possiamo usare questa idea per costruire un algoritmo per calcolare la radice quadrata di un qualunque numero n: basterà applicare il metodo alla matrice

Questa matrice infatti ha due autovalori distiniti 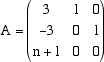e il metodo delle iterate approssima l'autovalore di modulo massimo: togliendo 1 al valore ottenuto abbiamo una approssimazione per .

Le iterate della matrice

permettono di calcolare, col metodo precedente, un valore approssimato della radice cubica di n. Il polinomio caratteristico della matrice A è infatti

che ha una sola radice di modulo massimo, la radice .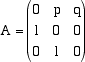

In generale la matrice

permette, tramite le sue potenze, di approssimare la radice di modulo massimo dell'equazione cubica

Esercizi (non alla portata di tutti)