|
Matematica discreta 2 Complementi ed esercizi dell'Unità 1. |
 |
Algoritmo per stabilire se due vettori numerici sono linearmente dipendenti
Consideriamo due vettori numerici a n compomenti x = (x1,x2, ... ,xn) e
y = (y1, y2 , ... ,yn). Ricordiamo che questi vettori sono sono linearmente dipendenti
se x = 0 o, se questo non è il caso, se esiste uno scalare k tale che La verifica di questo fatto e dunque estremamente semplice quando il numero n di componenti dei due vettori è piccolo, ma quando n è dell'ordine di grandezza di qualche centinaia o più la verifica a mano risulta talmente noiosa da indurre facilmente in errore. È in questa situazione che il calcolatore diventa essenziale. Il programma che proponiamo ha la struttura di un ordinogramma e può essere facilmente implementato con qualunque linguaggio di programmazione. In entrata abbiamo memorizzato il numero (intero) n che definisce il numero di componenti dei due vettori e due stringhe (x1,x2, ... ,xn) e (y1, y2 , ... ,yn) di numeri reali implementati con un dato grado di precisione. 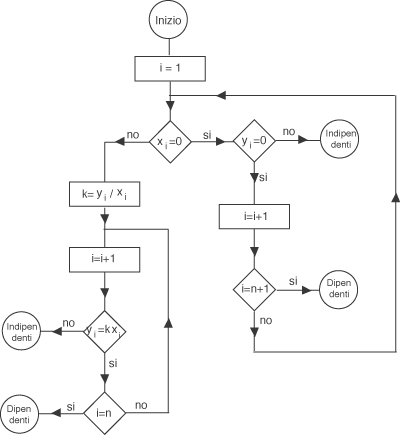
| |