Matematica discreta 2

Complementi ed esercizi dell'Unità 1.



Somma di due vettori geometrici

Dati due vettori geometrici u e v la loro somma u+v si rappresenta nel seguente modo:

  • si sceglie un qualunque punto A della spazio
  • si applica in A il vettore u e si trova il segmento orientato AB
  • si applica in B il vettore v e si trova il segmento orientato BC
  • Il segmento orientato AC ottenuto "sommando i due cammini" rappresenta un vettore che, per definizione è la somma di u e v.

È facile rendersi conto che se si cambia posizione al punto A e si eseguono le operazioni che abbiamo descritte a partire da un'altro punto A' dello spazio il risultato che otteniamo è un altro segmento orientato equipollente al primo. Il risultato dunque dipende solo dalla direzione, dal verso e dal modulo dei due vettori iniziali e non dalla posizione che scegliamo per calcolare la loro somma.
La figura animata seguente permette di modificare la direzione, il verso ed il modulo di due vettori u e v e di calcolare automaticamente la loro somma u+v. Cambiando la posizione di A il risultato è sempre un segmento orientato equipollente ad AC.

Figura animata

È molto utile per fissare delle corrette immagini mentali modificare più volte la figura animata per rendesi ben conto di come si possa sommare una direzione un verso e un modulo con un'altra direzione, un'altro verso e un'altro modulo. In particolare è utile, usando la figura animata del testo fare la somma di vettori con la stessa direzione e lo stesso verso, o con la stessa direzione e versi opposti o anche fare la somma di due vettori uguali

Prodotto di un vettore geometrico per uno scalare

La somma di n vettori uguali a v si indica con nv. In generale dato uno scalare a e un vettore v è possibile definire un nuovo vettore denotato con av che si chiama il prodotto di v secondo lo scalare a o anche il multiplo di v secondo lo scalare a. Il vuovo vettore av ha la stessa direzione di v, lo stesso verso se a > 0, il verso opposto se a < 0 e il modulo uguale al modulo di v moltiplicato per il modulo di a. In una formula il modulo di av è

|av| = |a||v|

È interessante notare come la moltiplicazione di un vettore geometrico per -1 ne cambi il verso lasciando inalterata direzione e modulo. Ne segue che, se moltiplichiamo un dato vettore geometrico due volte per -1, otteniamo il vettore di partenza. Dunque, in questo contesto geometrico, la regola dei segni si interpreta dicendo che cambiando due volte il verso di percorrenza di una retta si ottiene il verso di partenza. Questo fatto permette di dimostrare che

a(bv) = (ab)v

che insieme alle

(a+b)v = av + bv

a(v + w) = av + aw

permette di operare coi vettori geometrici come si opera coi numeri nell'aritmetica elementare.

Dati due o più vettori geometrici, u, v, ... ,w, una combinazione lineare dei vettori u, v, ... ,w è una espressione del tipo

au + bv + ... + cw

Gli scalari a, b, ... , c sono detti coeffcienti della combinazione lineare. Con una immagine legata alla statica, scienza dalla quale questi concetti hanno tratto origine, si dice anche che i vettori u, v, ... ,w sono stati presi con i pesi a, b, ... , c e sommati tra loro.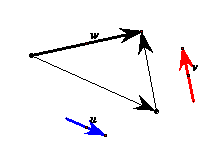

Cliccando sulla figura si apre una pagina animata che aiuta ad esercitarsi sul calcolo di combinazioni lineari di vettori. In fondo alla pagina sono proposti degli esercizi pratici da realizzare servendosi della figura animata. Questa pratica aiuta a svolgere correttamente e con facilità gli esercizi che proponiamo in fondo a questa sezione.

Esercizi