Geometria Algebrica
Dipartimento di Matematica - Università di Roma Tor Vergata

Gli oggetti di studio della Geometria Algebrica sono le

varietà algebriche

che sono, grosso modo, manifestazioni “geometriche” di soluzioni di sistemi di equazioni polinomiali in una o più indeterminate.

Esempi semplici di varietà algebriche sono le Curve Algebriche Piane, che includono ad esempio

· rette

· coniche (e.g. circonferenze, parabole, ellissi, iperboli),

· cubiche (come curve ellittiche),

· quartiche (come lemniscate),

· ovali di Cassini,

· eccetera

Un punto P del piano appartiene ad una curva algebrica C se le sue coordinate soddisfano un’equazione polinomiale F(x,y) = 0 detta equazione cartesiana di C.

(i) Domande di base in questi esempi elementari riguardano, ad esempio, lo studio di punti di “particolare interesse” di C, come i punti singolari, i punti di flesso od i suoi punti “all'infinito”.

(ii) Domande più avanzate, sempre in questa classe di esempi, riguardano la “topologia” di C e le relazioni tra le curve date da diverse equazioni.

Domande “classiche” più generali in Geometria Algebrica sono anche questioni enumerative; come ad esempio:

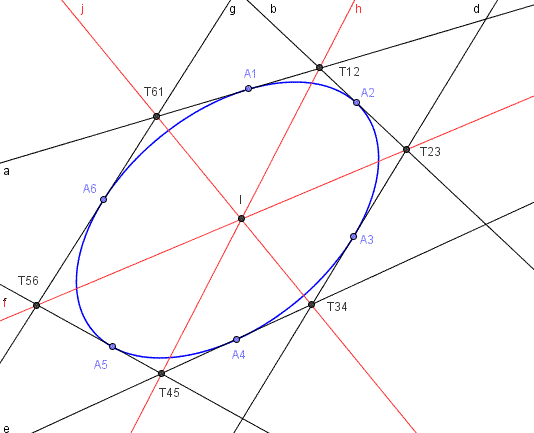
(a) quante coniche nel piano sono tangenti ad un dato insieme di rette?

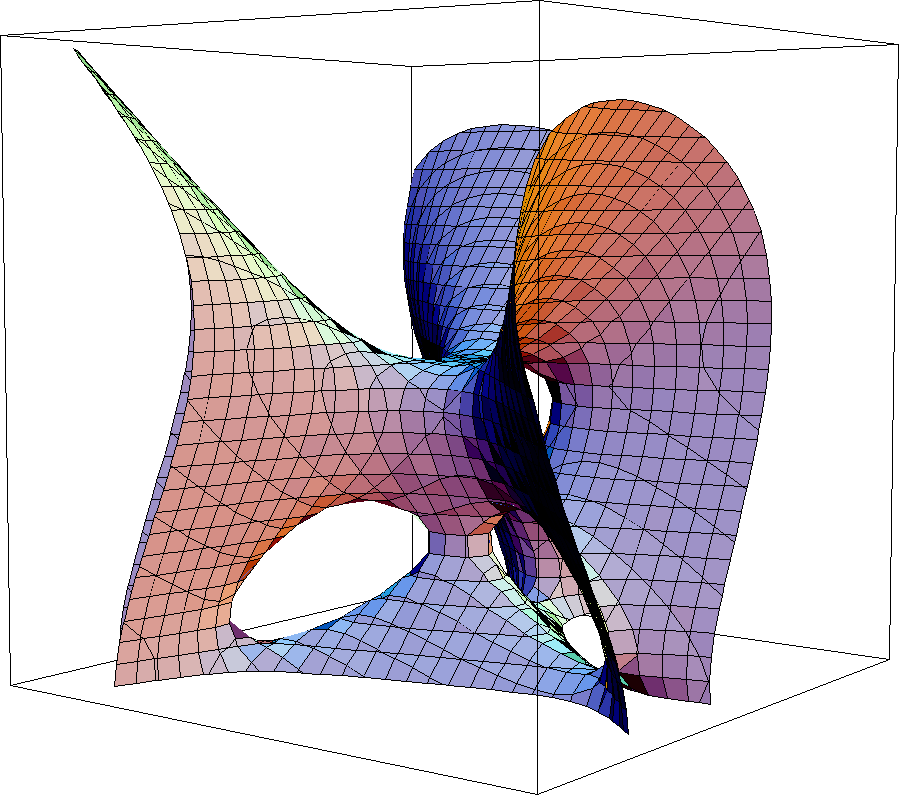
(b) quante rette sono contenute in una superficie cubica nello spazio proiettivo tridimensionale?

Tornando a questioni più generali della Geometria Algebrica, molte proprietà dei luoghi di zeri di polinomi diventano più “trasparenti” se si considerano le soluzioni di questi polinomi sui numeri complessi.

In questo ambito, possono essere applicati anche metodi provenienti da altre branche della Geometria come:

i. Topologia,

ii. Geometria Differenziale,

iii. Equazioni alle derivate parziali.

Questo e’ un fenomeno “caratterizzante” la Geometria Algebrica: proprio perché i polinomi sono “onnipresenti” in Matematica, la Geometria Algebrica si distingue come “crocevia” di molti campi diversi delle Scienze di base.

Un’esempio principe di questa interdisciplinarità è dato appunto dal caso delle Curve Algebriche: essenzialmente ci si riduce allo studio delle Superfici di Riemann compatte (punto di vista topologico, differenziale, analitico, algebrico, ecc.)

In tempi più attuali,

• lo studio dei punti di una varietà algebrica con coordinate razionali od in un campo di numeri ha dato vita alla Geometria Aritmetica, campo di studio della Teoria Algebrica dei Numeri;
• l'utilizzo di computers ha dato vita all'area della Geometria Algebrica Computazionale che consiste nello sviluppo di algoritmi e software utili per studiare e trovare proprietà di varietà algebriche esplicite date (e.g. Varietà toriche);
• recenti sviluppi nella fisica delle alte energie hanno portato ad una serie di importanti risultati e di problemi aperti nella Geometria Algebrica (e.g. Mirror Symmetry)
• ecc.

Gran parte dello sviluppo della Geometria Algebrica si è verificato, nel secolo scorso, in un contesto algebrico “astratto”, con sempre maggiore enfasi sulle proprietà "intrinseche" delle varietà algebriche, i.e. di quelle proprietà che non dipendono da alcun particolare modo di vedere la varietà immersa in uno spazio ambiente di coordinate.

Uno dei risultati principali di questo approccio intrinseco alla Geometria Algebrica è la teoria degli

schemi

Questa teoria è ottenuta estendendo la nozione di punto.

- In Geometria Algebrica classica, un punto di una varietà affine X può essere identificato, mediante il Nullstellensatz di Hilbert, con un ideale massimale dell'anello delle coordinate A(X) di X;

- i punti del corrispondente schema affine X sono tutti gli ideali primi di A(X); ciò significa che un punto dello schema X può essere sia un punto, nel senso usuale, che un “sottoschema” o sottovarietà di X.

Quest’approccio algebrico astratto ha inoltre il pregevole risvolto di permettere un'unificazione del linguaggio e degli strumenti della Geometria Algebrica classica, principalmente rivolta ad i punti complessi di X, con quello della Teoria Algebrica dei numeri.

Esempio della potenza di tale approccio è la dimostrazione di Wiles della congettura di lunga data chiamata Ultimo Teorema di Fermat

Alcune delle figure principali per lo sviluppo della moderna Geometria Algebrica sono ad esempio

- Oscar Zariski,

- André Weil,

- Jean-Pierre Serre,

- Alexander Grothendieck,

- ecc.

Un'importante questione di fondo, che ha fortemente motivato questo approccio più “algebrico astratto” alla Geometria Algebrica, è il seguente:

cercare di “mettere insieme” tutte le varietà algebriche di una data tipologia di modo che esse siano “parametrizzate” da punti di uno “spazio” che è a sua volta una varietà algebrica.

Se esiste, un tale spazio viene chiamato

Spazio di moduli

Semplici esempi di “spazi di moduli” sono

a)gli spazi proiettivi (che parametrizzano sottospazi vettoriali di dimensione 1 in un dato spazio vettoriale);

b)loro naturali generalizzazioni come le Grassmanniane.

“Problemi di moduli” di oggetti geometrici più “elaborati”, sono ad esempio:

• classificare tutte le curve algebriche di un certo “tipo”;
• classificare tutti i fibrati vettoriali di una determinata tipologia su una varietà algebrica X fissata;
• ecc.

Gli obiettivi comuni di tutte queste domande sono:

(a) costruire

(b) descrivere

lo Spazio di moduli di tali oggetti.

E’ proprio per affrontare queste costruzioni, che la Geometria Algebrica si è via via trasformata dai suoi inizi “classici” di Geometria Proiettiva in un soggetto sempre più intrinseco, attingendo ad una vasta gamma di idee in molteplici branche della Matematica come

- l'Algebra Commutativa,

- l'Algebra Omologica,

- la Teoria delle Categorie,

- ecc.

Uno degli spazi di moduli più studiati, eppure tutt’ora ricco di molteplici questioni aperte, è lo

spazio dei moduli delle curve algebriche (o superfici di Riemann) di genere g