Metodi numerici per le scienze biomediche
(4 crediti, II semestre, inizio: 2 Maggio 2007)
Appelli: 11 Luglio 2007 e 19 Settembre ore 12.
E' obbligatorio iscriversi all'appello via EMAIL al docente!
Laurea Specialistica in
Matematica per le applicazioni
(il corso e' fortemente sconsigliato in laurea triennale)
Propedeudicità:
un corso introduttivo per le equazioni a derivate parziali, metodi
numerici per equazioni a derivate parziali; fortemente consigliato
algebra lineare numerica ma non obbligatorio.
Argomenti: Soluzione
numerica di equazioni di convezione-diffusione-reazione nonlineari
dipendenti dal tempo nelle applicazioni
biomediche, fisiche e chimiche.
Settori: MAT/08 (analisi numerica), BIO/07 (Ecologia), BIO/10
(Biochimica), ING-INF/06 (Bioingegneria)
Docente:
D.
Bertaccini
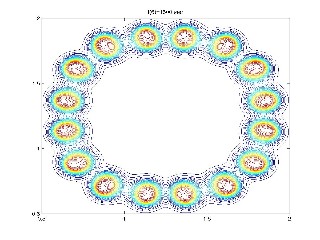
Formazione di pattern con un modello di Gray-Scott 2D, seconda
componente, t=1500s (trasformato in un
sistema di 80000 equazioni differenziali ordinarie)
Orario. Lun,Merc,Giov. 14-16 Aula F
Ricevimento: su appuntamento.
Generalita'. Il corso e' rivolto principalmente agli
studenti del Corso di Laurea in Matematica, Fisica,
Chimica, Biologia, Ingegneria.
Il corso ha come prerequisito l'aver seguito un corso base di algebra
lineare
numerica, teoria degli errori e algebra lineare di base (esempio:
Analisi
Numerica tenuto dal Prof.
Pasquini) e di metodi numerici per equazioni differenziali ordinarie
(il modulo di base di Analisi Numerica che tratta integrazione e
interpolazione e' sufficiente). Non sono previste esercitazioni
guidate a laboratorio anche se e' consigliato realizzare almeno una
parte dei modelli che tratteremo per proprio conto per capire piu' a
fondo la natura dei modelli, le interazioni con il modello continuo, la
stabilita', la convergenza alle soluzioni del modello continuo, ecc.
Scopo. Nella prima (e di maggior peso) parte del corso si
vogliono analizzare alcuni modelli per le scienze applicate e trattare
i corrispondenti modelli numerici. In particolare, ci si
interessera' alla soluzione numerica di sistemi di equazioni a derivate
parziali (PDE)
di tipo convezione-diffusione-reazione nonlineari dipendenti dal tempo.
Modelli di questo tipo sono molto frequenti in medicina, in biologia e
in chimica.
La soluzione numerica
dei suddetti problemi (ad esempio per studiare quello che succede in
tempi lunghi ad una soluzione) offre vari gradi di difficolta', tra cui
(1) la presenza di differenti scale spazio/temporali spesso per molti
ordini di grandezza e (2) la soluzione di problemi
discreti di grandissime dimensioni, cosa che pone formidabili
difficolta'
pratiche.
Programma del corso. Il programma di massima e':
Modelli e metodi numerici
per sistemi di equazioni di convezione-diffusione-reazione nonlineari
(Richiami ai) metodi numerici per la soluzione di equazioni
differenziali ordinarie di tipo STIFF
Modelli e metodi numerici per PDE di evoluzione lineari e non lineari e
loro
proprieta'
Equazioni di evoluzione di tipo trasporto-diffusione-reazione
Modello e metodi numerici per chimica dell'atmosfera e trasporto di
inquinanti
Modello e metodi numerici per la thermal ablation guidata da NMR
Metodi numerici per pattern formation. Applicazione al modello di
Gray-Scott 1D e 2D
Modello di Keller e Segel e metodi numerici per la chemotassi
Testi consigliati. I testi consigliati per il corso
sono:
Bibliografia:
W. Hundsdorfer, J.G.
Verwer, Numerical Solution of TIme-dependent
Advection-Diffusion-Reaction Equations, Springer, 2003.
D. Bertaccini, dispense del corso..
Il docente. Il suo principale interesse scientifico e'
proprio
la messa a punto e analisi di metodi per la soluzione di problemi
dipendenti dal tempo e la soluzione di problemi discreti di grandi
dimensioni. Alcune informazioni sul docente si trovano nella sua homepage.
