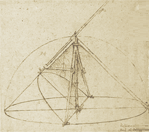
Tra gli argomenti che verranno trattai durante la conferenza del prof R. Rashed ha molta importanza il metodo usato dai matematici arabi e in particolare da Al-Khayyam per risolvere le equazioni algebriche di grado minore o uguale a tre. Per le equazioni cubiche il metodo consiste nel ridurre la ricerca della soluzione alla ricerca del punto di intersezione di due coniche. Al Khayyam classifica tutti i possibili tipi di equazioni algebriche a coefficienti positivi in 25 tipi secondo lo schema allegato e per ogni tipo, nel caso cubico, indica le coniche da utilizzare per risolvere l'equazione. E' utile confrontare questo metodo con quello utilizzato secoli dopo da Bombelli anche perché entrambi metodi permettono, attraverso la visualizzazione dinamica, una concettualizzazione plurimodale, di un tipo di problema la cui risoluzione oggi di norma avviene solo con l'applicazione di appropriati schemi di calcolo. Per questa caratteristica, che ci sembra estremamente utile da un punto di vista didattico, la trattazione di alcuni problemi di al-Khayyam è tra gli argomenti del Laboratorio collegato al corso SSIS ''Processi cognitivi e didattica della matematica'' tenuti dalla prof.ssa Laura Catastini e dal prof. Franco Ghione.

In questa introduzione prendiamo in esame una particolare equazione di terzo grado, l'equazione

x³ = a²(x+b)

e confrontiamo tra loro i due metodi risolutivi. Il coefficiente della x viene scritto come un quadrato per rendere omogenea l'equazione. E' chiaro che, se tale coefficiente è positivo, questa scrittura non è restrittiva sul tipo di equazione.

Come è noto, l'approccio di Bombelli segue il metodo di Tartaglia e di Cardano che si basa sullo sviluppo del cubo del binomio

(A+B)³ = A³ + B³ + ³AB(A+B)

L'idea è quella di dividere l'incognita x in due parti A e B e di utilizzare la formula precedente,

x = A + B
A³ + B³ = a²b
3AB = a²

Elevando al cubo la terza relazione abbiamo che, delle due nuove incognite A³ e B³, conosciamo la somma e il prodotto: la somma è a²b mentre il prodotto (a²/3)³. Questo ci permette di scrivere una nuova equazione in T (detta equazione risolvente) le cui due soluzioni sono appunto A³ e B³. Tale equazione i cui coefficienti sono dati dall'equazione iniziale, è

T² - a²b T + (a²/3)³ = 0

espressione che diventa negativa se b è piccolo rispetto ad a. In questo caso Bombelli, con grande ardire intellettuale, anche se la radice di un numero negativo non esiste, prosegue il calcolo e trova comunque una radice positiva all'equazione cubica data. Tale radice esiste? esiste sempre comunque siano i coefficienti a e b?
Per convincersi di questo Bombelli propone una costruzione geometrica con la quale risulta sempre possibile trovare un segmento la cui lunghezza è, in una assegnata unità di misura, la soluzione positiva all'equazione proposta.
La figura animata seguente permette di modificare i vari segmenti fino a trovare la soluzione.

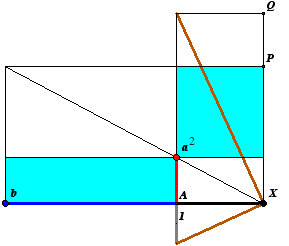
Si possono muovere col mouse i punti a e b modificando i parametri dell'equazione. L'unità di misura è il segmento grigio. Il lunghezza del segmento AX rappresenta l'incognita x e può essere modificato agendo col mouse sul punto X.
Costruiamo su X un triangolo rettangolo (marrone nella figura). Per il II teorema di Euclide, l'altezza del triangolo vale x, e le proiezioni sull'ipotenusa sono 1 e x². Ne segue che il segmento XQ vale x² e l'area del rettangolo AQ vale x³. Questa area rappresenta dunque il primo membro dell'equazione. Osserviamo ora che i due rettangoli azzurri hanno (per il teorema dello gnomone) area a²b essendo il segmento blu di lunghezza b e il segmento rosso di lunghezza a². Ne segue che il rettangolo AP ha area a²b + a²x. Essa rappresenta dunque il secondo membro dell'equazione. La soluzione si trova quando P=Q. Situazione che possiamo riprodurre muovendo col mouse il punto X fino a far coincidere P e Q. Si vede dunque che comunque siano scelti i parametri a e b una soluzione si può sempre trovare, anche quando b è molto piccolo rispetto ad a e il D è negativo.

Vediamo ora il metodo di Al Khayyam.
Invece di cercare direttamente la soluzione x dell'equazione

x³ = a²(x+b)

introduciamo una nuova variabile y e cerchiamo una soluzione (x,y) del seguente sistema di due equazioni in due incognite

Se troviamo una coppia ordinata di numeri (x,y) che verifica simultaneamente le due equazioni, allora la x verifica l'equazione proposta. Infatti, elevando al quadrato ay e moltiplicando la seconda equazione per a², troviamo a²y²=x⁴ e anche a² y² = a²x(x+b), da cui x⁴ = a²x(x+b) e, se x non è zero, x³ = a²(x+b). Dunque il problema di trovare la soluzione x dell'equazione proposta è ridotto al problema di trovare una soluzione (x,y) del sistema in due equazioni in due incognite. Il nuovo problema che potrebbe sembrare più complicato può essere però interpretato geometricamente e quindi studiato con altri metodi. Infatti se interpretiamo le coppie ordinate (x,y) come coordinate di un punto del piano cartesiano, la prima equazione è soddisfatta dai punti (x,y) che si trovano su una parabola con vertice nell'origine e asse di simmetria verticale, mentre la seconda dai punti (x,y) che si trovano su una iperbole equilatera che ha come asintoti le bisettrici dei quadranti. Queste curve possono essere facilmente disegnate per punti utilizzando la teoria delle proporzioni. La prima curva è data dalle coppie di numeri (x,y) tali che x èmedio proporzionale tra y e a

a : x = x : y

x : y = y : (x+b).

Le soluzioni (x,y) del sistema sono dunque i punti del piano comuni alle due curve, i punti cioè nei quali le due coniche si incontrano. Non è difficile disegnare con un software di geometria dinamica questi medi proporzionali e dunque disegnare le due curve e vedere dove si incontrano. Il medio proporzionale tra A e B infatti non è altro che l'altezza rispetto all'ipotenusa, del triangolo rettangolo per il quale le proiezioni dei cateti sull'ipotenusa sono i segmenti A e B. La seguente figura animata realizza la parabola ay = x².

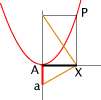
Possiamo modificare col mouse la posizione del punto X e del parametro a: AX risulta in ogni situazione medio proporzionale tra a e XP.

L' iperbole equilatera si può costruire in modo analogo.
Il segmento AX rappresenta, come sempre l'ascissa, e il cerchio grande, che ha centro in X, riporta il segmento di lunghezza x+b di seguito a x in modo che XQ sia il medio proporzionale tra x e x+b.

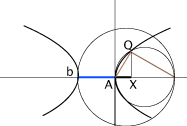
Spostando col muose il punto X possiamo vedere come si costruisce l'ordinata XQ e spostando il punto azzurro possiamo cambiare il parametro b e modificare la forma dell'iperbole.

Sovrapponendo infine le due coniche , la soluzione dell'equazione si trova quando P coincide con Q.

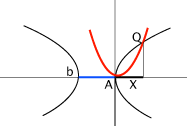
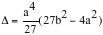
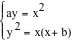
Notiamo che quando b è abbastanza piccolo rispetto ad a la parabola interseca l'iperbole in 4 punti, che escludendo il valore x=0, da tre soluzioni reali dell'equazione: una positiva e due negative. Paradossalmente proprio quando la formula risolutiva di Cardano da dei problemi col 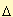negativo , proprio in quel caso le soluzioni reali sono tre. Il metodo di Al Khayyam che permette di costruire le soluzioni per via geometrica apre la strada a formidabili sviluppi sia in campo topologico (esistono punti di intersezione? se l'iperbole entra nella parabole deve anche uscirne?) che verso la moderna geometria algebrica (lo studio della geometria dell'insieme delle soluzioni di sistemi di equazioni polinomiali).