LABORATORIO VIII

• Indice del laboratorio
  • Analisi prospettica di alcuni quadri del tre-quattrocento.
  • Esercizio: analisi prospettica di un quadro del '400

Laura Catastini

• Obiettivi disciplinari e formativi della lezione
  • Analisi prospettica guidata di alcuni quadri del tre-quattrocento. per individuarne la correttezza geometrica dell'impianto prospettico e la presenza o meno dei canoni albertiani
  • Si chiede agli studenti di verificare graficamente, su una tavola a colori con la riproduzione di un quadro del '400, se questa soddisfa i canoni albertiani e se è prospetticamente corretta. Devono poi procedere alla ricostruzione del punto di vista e delle altezze. Si chiede infine di ricostruire la pianta dell'ambiente e le posizioni reali su di esso degli oggetti rappresentati. Nella verifica si impiegano anche strumenti di calcolo, integrando gli elementi di laboratorio visti nell'arco dell'intero progetto.
  • Applicazione degli elementi fin qua presentati, in un problema di ricostruzione della realtà, data la sua rappresentazione prospettica e alcune misure.

SVOLGIMENTO LABORATORIO

Si presentano al proiettore quadri dell'epoca in stile albertiano mostrando come si effettua la verifica della correttezza della resa prospettica.

Analisi 1.
Analizza l'impianto prospettico della seguente pittura di Masolino datata 1425 alla luce del metodo albertiano



Successivamente la scheda 1 viene rimossa e si consegna la Tavola VII-2a degli esercizi. Il primo di essi chiede di orientarsi nel disegno e di mettere i nomi agli oggetti indicati

Verifica 1.
Determinare il punto centrico, la linea dell'orizzonte e verificare se il quadro è stato realizzato seguendo l'impianto descritto da Alberti.



Possiamo intanto verificare se le linee di profondità concorrono ad un punto. Abbiamo fatto questa verifica per alcune linee e la cosa è verificata. In questo modo possiamo individuare il punto centrico e la linea dell'orizzonte. Vediamo che gli occhi di tutti i personaggi in piedi sono allineati sulla linea dell'orizzonte. Questo corrisponde all'aver scelto, come suggerisce Alberti, l'altezza del punto centrico sul piano di terra corrispondente all'altezza di un uomo che viene approssimata a tre braccia.

Domanda 2.
Calcolare usando il metodo delle "alzate" l'altezza della nicchia sulla destra dove giace l'inferma.



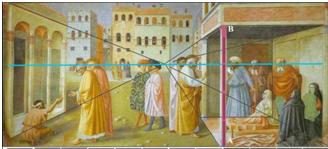
L'altezza AC corrisponde a 3 braccia e facendo la proporzione AB risulta di circa 4 braccia e mezzo. La nicchia appare quindi con una pianta quadrata di lato 4 braccia (dal momento che i due rettangoli rappresentati sui due muri interni paiono ragionevolmente uguali) e di altezza pari a circa 4 braccia e mezzo.

Verifica 3.
Verificare se le colonne sulla sinistra del quadro, supponendole alla stessa distanza, sono degradate in modo prospetticamente corretto.
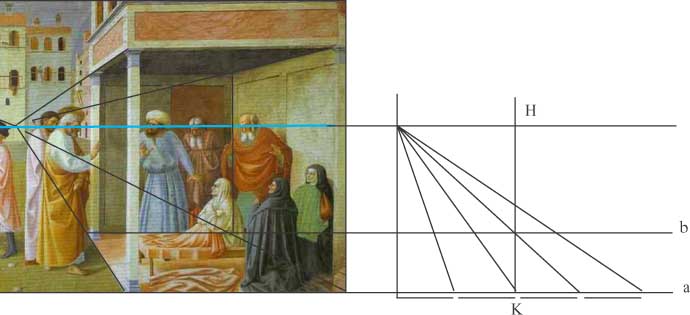
Disegniamo sulla sinistra del dipinto la costruzione ausiliaria del modo ottimo di Alberti, cioè:

• il prolungamento della linea di terra, sul quale segniamo un certo numero di tacche uguali, di misura a piacere
• sulla verticale, a un estremo di questo prolungamento, prendiamo il punto all'altezza della linea dell'orizzonte
• congiungiamo questo punto con ogni tacca del prolungamento della linea di terra
• dal piede di ogni colonna tiriamo le parallele a, b, c, d, alla linea di terra. Queste parallele intersecano ognuna i segmenti congiungenti.



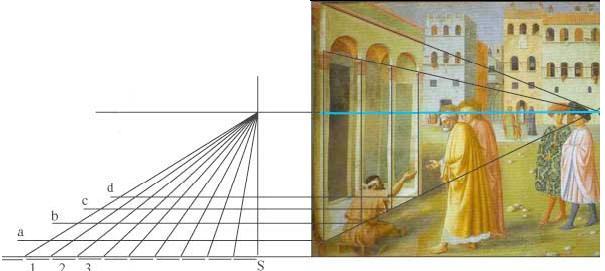
Le tacche rappresentano in una scala arbitraria la distanza tra gli elementi orizzontali prescelti, in questo caso due colonne consecutive. Le linee orizzontali a,b,c, d sono le linee sulle quali poggiano le 4 colonne sul quadro. Se esse sono correttamente distanziate deve esistere un segmento verticale HK che interseca 4 linee oblique consecutive alle stesse altezze alle quali si trovano le orizzontali a,b,c,d. Infatti sarebbe in questo modo, che secondo la procedura di Alberti, si debbono degradare le linee trasverse. Spostando sul disegno la linea verticale HK con un righello. troviamo una posizione, quella rappresentata nel disegno, che corrisponde a quanto detto: il righello è perfettamente allineato con i punti di intersezione tra le linee trasverse e quelle di congiunzione co le tacche in scala.



che lo pavimentano con quadrati di una grandezza nota, non possiamo, usando questa parte del quadro, esplicitare numericamente questa distanza, possiamo solo rapportarla a quella che separa due colonne.

Analisi 2
Il seguente dipinto di Beato Angelico realizzato a meta del '400 segue molto da vicino le indicazioni di Alberti. Lo stesso Angelico aveva probabilmente conosciuto Alberti a Roma e sembra fosse a conoscenza delle "modo ottimo". In questa Presentazione la linea centrica e tracciata all'altezza degli occhi dei personaggi e il degradare delle colonne, come risulta dalla nostra ricostruzione prospettica, sembra realizzata con le procedure albertiane.



Per verificare la correttezza prospettica del dipinto abbiamo tracciato a destra lo schema del modo ottimo, (vedi sopra, analisi 1) e abbiamo cercato una linea verticale che riuscisse a traguardare i punti diagonali di tutte le linee trasverse su cui si appoggiano le colonne. Abbiamo visto che, dopo 5 tacche, la verticale aveva esattamente la proprietà richiesta. Ne possiamo dedurre che, l'impianto della pittura è costruito considerando il punto centrico a una altezza di tre braccia sulla linea di terra (perché i personaggi raffigurati sono alti tre braccia, stanno in piedi sul pavimento orizzontale e hanno gli occhi in corrispondenza alla linea di terra). In più, possiamo dire che la distanza dell'occhio dal quadro è 5 volte la distanza tra due colonne consecutive.



Analisi 3
Analizza l'impianto prospettico della seguente Annunciazione di Raffaello dipinta nel 1502 alla luce del metodo del punto di distanza di Piero della Francesca cercando di ricostruirne la pianta.



Cominciamo col cercare il punto principale e la linea dell'orizzonte tracciando alcune linee corrispondenti alle linee di profondità. Supponiamo poi, ragionevolmente, che la base su cui poggia il cerchio del piede delle colonne sia un quadrato. Congiungendo i punti sulle diagonali dei trapezi rosa ci accorgiamo che queste sono allineate con quelle dei quadrati bianchi individuati dalle colonne e convergono allo stesso punto sulla linea dell'orizzonte e quindi anche i trapezi rosa rappresentano dei quadrati. Disegniamo per ricostruzione una parte della pianta:



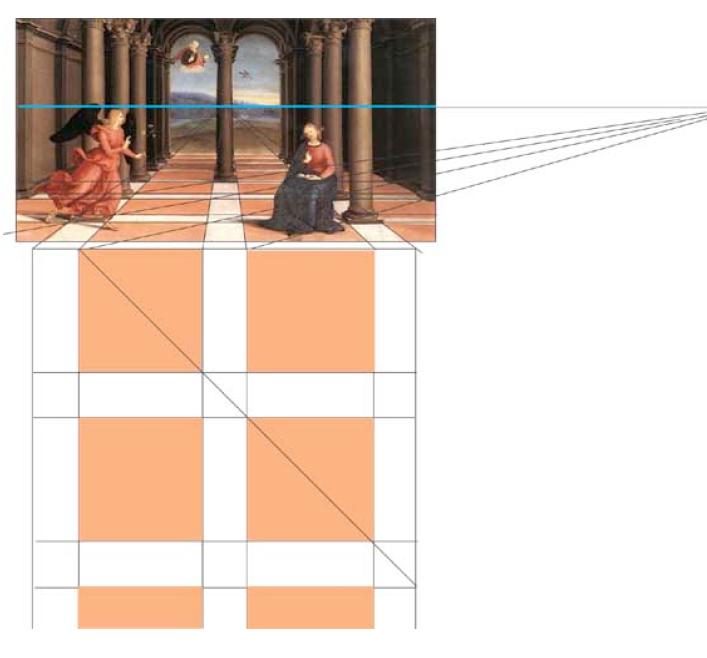
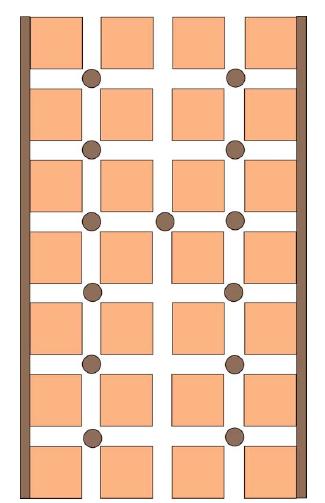
Una volta capita la geometria del pavimento, la pianta deriva semplicemente dal computo del numero di colonne visibili e piastrellature.



Esercizio di analisi di un quadro
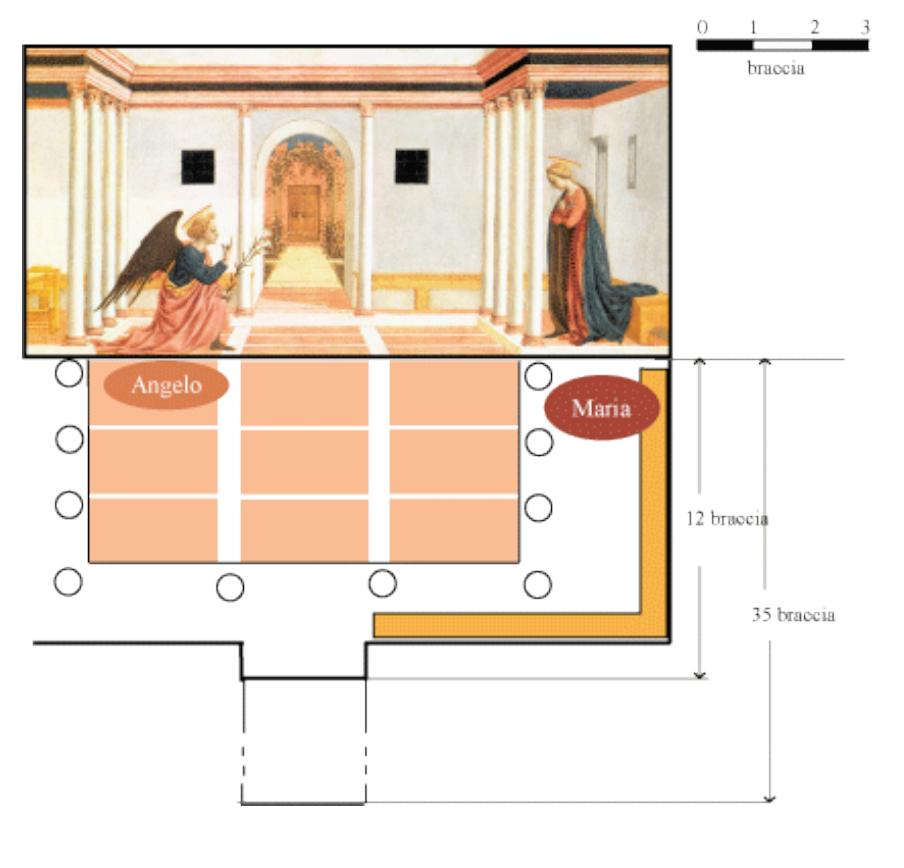
Si consegna una riproduzione a colori del seguente dipinto di Domenico Veneziano, Annunciazione (1445), e una tavola in bianco e nero sulla quale lavorare (Tavola VIII-1), chiedendo di fare l'analisi dell'impianto albertiano e di ricostruire la pianta dell'ambiente. Nella Tavola VIII-2 si può vedere quanto realizzato in media dagli studenti.



Studio completo dell'Annunciazione di Domenico Veneziano

La determinazione del punto centrico e della linea dell'orizzonte si esegue facilmente tracciando le immagini delle linee di profondità.



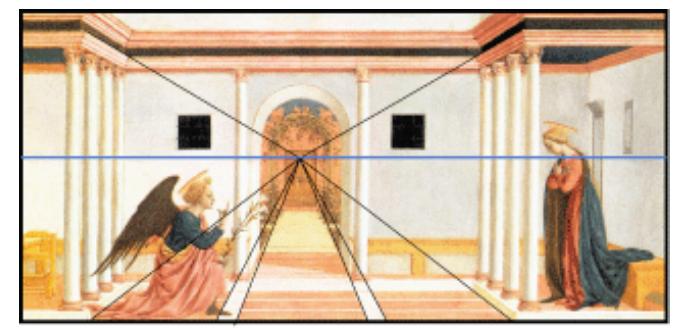
Per vedere l'altezza dell'occhio rispetto al piano di terra vediamo la situazione sul piano verticale che contiene la porta. L'immagine seguente ingrandisce la porta.



Se il punto centrico fosse stato posto più in alto (o più in basso) il punto di vista sarebbe stato più alto (o più basso) dell'altezza di un uomo. Gli occhi della Madonna sono più in alto della linea dell'orizzonte perché è sopra un gradino mentre quelli dell'angelo sono più in basso essendo inginocchiato.
Vediamo ora la situazione in primo piano.



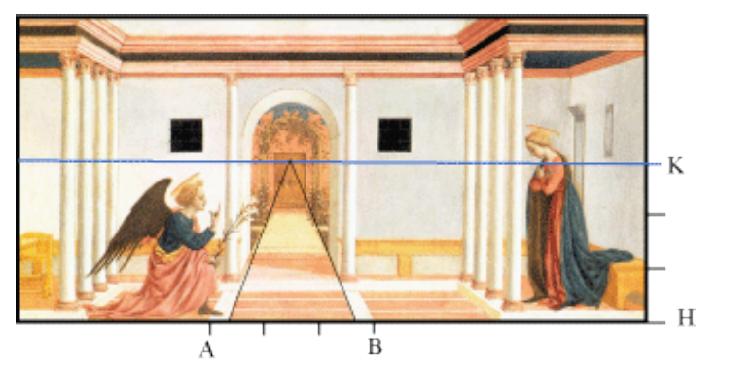
HK corrisponde a 30 braccia , AB= HK e quindi la larghezza della mattonella rossa è circa, in braccia, 3-2/3=7/3.
Per vedere a che distanza dal primo piano si trova l'occhio cerchiamo sul prolungamento della linea dell'orizzonte il punto di distanza supponendo che il mattonato rosso del pavimento sia fatto da quadrati. Per fare questo scegliamo una qualunque diagonale e prolunghiamola fino ad incontrare l'orizzonte. Misuriamo la distanza dal punto centrico: C è il punto centrico e D il punto di distanza.



Abbiamo 10 tacche (ognuna di tre braccia) che corrispondono a 30 braccia. Abbiamo quindi individuato la posizione dell'occhio: 3 braccia di altezza dal piano di terra e 30 braccia di distanza dal primo piano. Per trovare la distanza della porta dal primo piano e la lunghezza in profondità del porticato dobbiamo calcolare la lunghezza dei due rettangoli che compongono il vialetto.



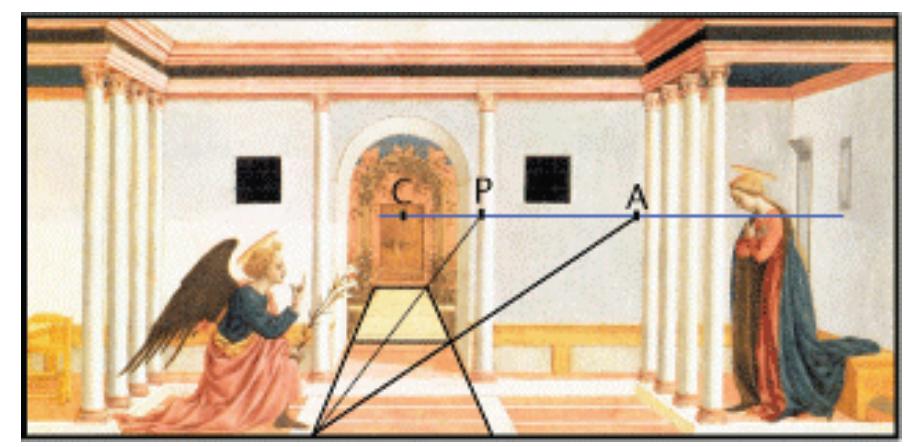
Le diagonali di questi rettangoli incontrano la linea dell'orizzonte nel punto P e nel punto A che rappresentano l'immagine del punto all'infinito delle corrispondenti rette del piano di terra. Dato che CA rappresenta tre braccia possiamo assumere che CP sia un terzo di CA cioè un braccio. Vediamo ora la situazione su piano dell'orizzonte



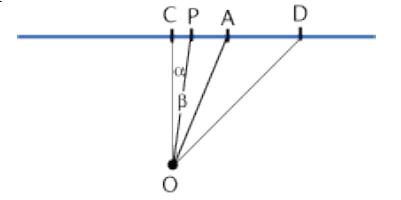
O e la posizione dell'occhio, C il punto centrico e D il punto di distanza, OC = CD. (nella figura, per ragioni tipografiche, non sono rispettati i rapporti dato che, in realta CD=10CA). CP= 1 braccio. Il raggio OP e il raggio di fuga della diagonale del rettangolo lungo mentre OA e quello del 9 porticato, gli angoli α e β rappresentano rispettivamente l'inclinazione della rispettive diagonali rispetto alle linee di profondita. Risulta

tan (α) = 1/30 , tan (β) = 1/10

Possiamo ora descrivere la situazione sul piano di terra.




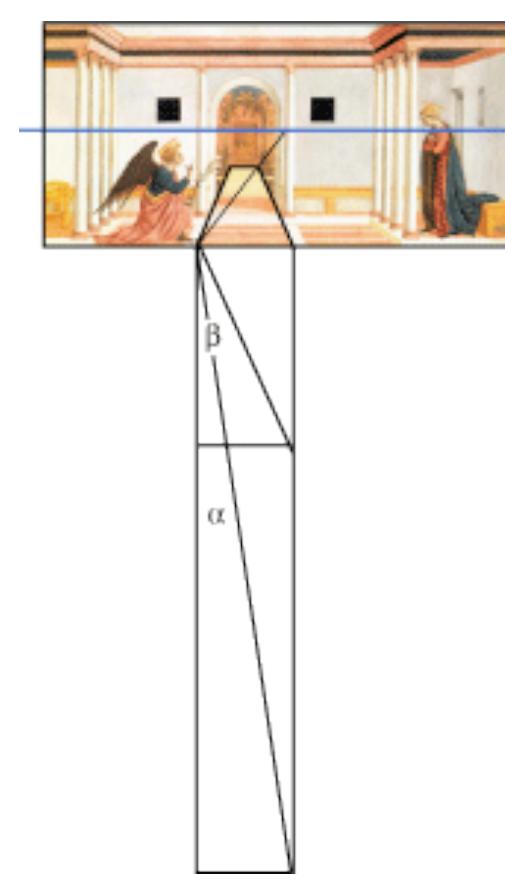
La lunghezza del viale e 30 volte la sua larghezza cioe 30(7/3) = 70 braccia, circa 40 metri, mentre la lunghezza del porticato e 10 volte la sua larghezza cioe 70/3= 23 +1/3.
Possiamo ora ricostruire la pianta



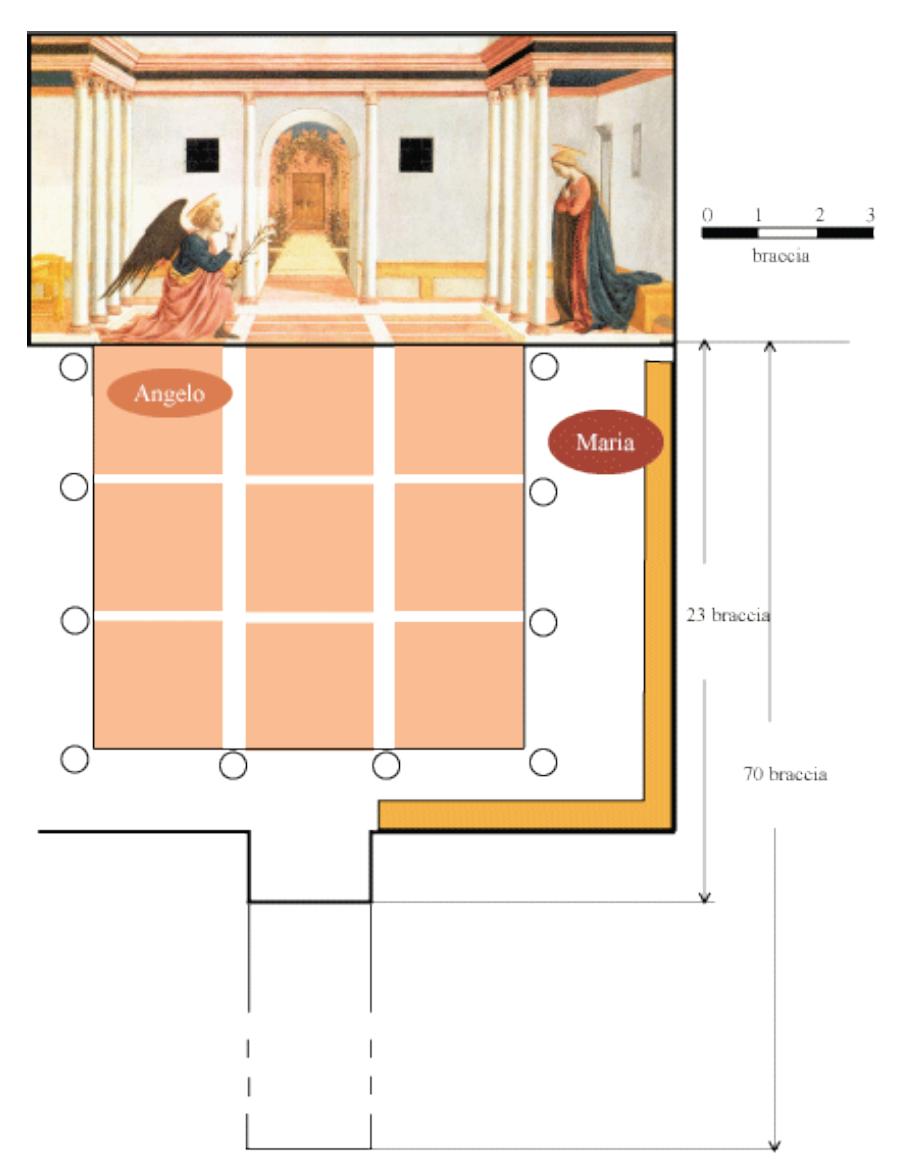
La ricostruzione della scena reale e della pianta è stata fatta supponendo che il mattonato rosso fosse nella realtà formato da mattonelle quadrate. Occorre, per ricostruire esattamente la realtà rappresentata, assumere che una data figura (ad esempio un quadrangolo) nella realtà abbia una determinata forma. A seconda di quale ipotesi viene formulata, la ricostruzione è diversa. Se supponiamo, ad esempio, che le mattonelle siano rettangolari, nel rapporto 1:2 la situazione cambia. Il punto D che avevamo trovato nell'ipotesi di mattonelle quadrate corrisponde ora al punto all'infinito della diagonale di una mattonella rettangolare e il nuovo punto di distanza D' di trova a metà. Sul piano dell'orizzonte abbiamo



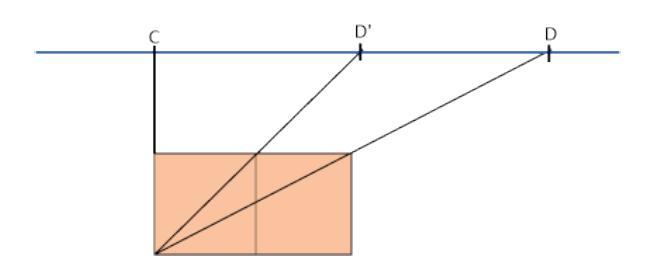
La distanza dell'occhio dal primo piano è ora 15 braccia e tutte le misure di profondità vengono dimezzate. La nuova pianta risulta