-
Indice del laboratorio
-
Il "vedere allineato" e il "vedere convergente",
l' "apparire" di rette parallele.
-
Il teorema 6 con dimostrazione nel caso di appartenenza dell'occhio al piano di terra.
Studio di come appaiono rette parallele.
-
Passaggio dalla visione diretta alla rappresentazione su un quadro.
-
Raggio di fuga, Punto di fuga.
-
Raggio di fuga principale, Punto di fuga principale.
-
Raggio di distanza, Punto di distanza.
-
Linea dell'orizzonte come linea di punti di fuga.
-
Estensione del piano euclideo con i punti all'infinito e la retta all'infinito.
-
Linee orizzontali e verticali nella rappresentazione prospettica.
-
Il quadro e la prospettiva.
Laura Catastini
-
Obiettivi disciplinari e formativi della lezione
Questa lezione contiene due punti cruciali:
-
L'individuazione dell'unica invariante della trasformazione prospettica, l'allineamento. Si può
descrivere concretamente le situazioni da definire con il prospettimetro, arrivando a una definizione
condivisa.
-
Il passaggio cognitivo-geometrico dalla visione diretta a quella prospettica. Nelle lezioni
precedenti il focus degli argomenti proposti era "l'angolo visivo", strumento centrale che permette
l'indagine matematica della trasformazione visiva. Ancora nel teorema 6 dell'Ottica siamo in
questo contesto, la dimostrazione si fonda sulla misura dell'angolo che sottende i "segmenti di
distanza" tra rette parallele. Nel passaggio alla visione prospettica e alla relativa geometria, è
necessario spostare l'attenzione dall'angolo visivo al raggio visivo, che diventerà il nuovo focus
cognitivo. Verrà così illustrato l'andamento dei raggi visivi che seguono rette parallele tra loro, il
loro tendere allo stesso raggio di fuga giacente sul piano dell'orizzonte, oggetto limite di questo
andamento. Si ricorderà come nella lezione precedente sia stata dimostrata l'equivalenza visiva
(Lab. IV, pg 10) tra tutti i punti dello spazio colti da uno stesso raggio e verrà posta l'attenzione ai
punti di intersezione dei raggi col piano del quadro, considerati come elementi rappresentanti di
queste classi di equivalenza, e che saranno chiamati punti proiettati. Il tendere al proprio raggio di
fuga dei raggi visivi che percorrono un fascio di rette parallele sul piano di terra (dominio), si
concretizza così nel tendere di punti proiettati sul piano del quadro (codominio) a un determinato
punto di fuga, che appare al finito. La ricerca del corrispondente elemento nel dominio di questo
punto di fuga porterà a un modello mentale dinamico che supporterà adeguatamente la definizione
di punto all'infinito e quella conseguente di retta all'infinito. L'uso del prospettimetro e di una
cornice vuota che simula virtualmente il piano del quadro, lasciando però passare i "fili" visivi,
aiuta la formazione di questi modelli mentali mediante il concreto operare dello studente con gli
elementi in gioco, permettendo un gioco immaginativo geometricamente corretto anche se
ovviamente non esaustivo riguardo al problema e assolutamente coerente con il successivo
sviluppo della teoria in ambito universitario.
SVOLGIMENTO LABORATORIO
Sappiamo dalla geometria euclidea che più punti sono allineati se per essi passa una retta e che
data una retta e un punto fuori di essa, esiste solo un piano che contenga la retta e il punto. Ne
deriva che se guardiamo punti allineati tra loro, i raggi visivi che colgono questi punti giacciono
tutti su uno stesso piano, insieme all'occhio (fig. 1).
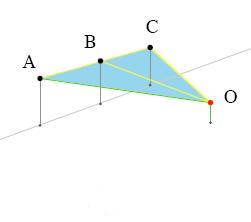
Fig.1
Sappiamo anche, per esperienza diretta, che linee rette sono viste sempre come linee rette, che non
cambiano forma secondo il punto di vista, come avviene per le altre forme geometriche.
Accade a volte, invece, che vediamo come allineati punti che non lo sono. Pensiamo alle
costellazioni celesti, per esempio la costellazione di Orione. Se guardiamo Orione nel cielo
notturno, (fig. 2) possiamo vederne al centro tre stelle in file, che paiono approssimativamente
allineate. La costellazione rappresenta un guerriero e le tre stelle al centro la sua cintura (fig. 3).
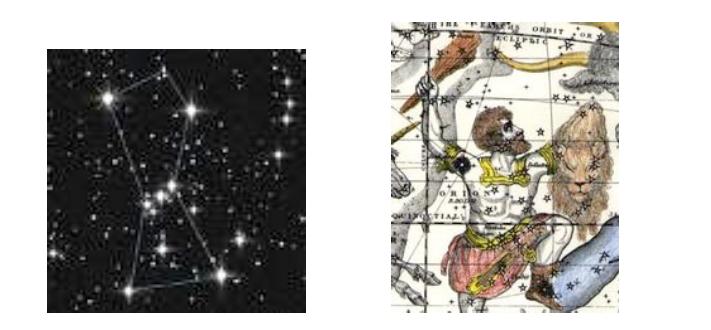
Fig.2 e Fig.3
Le stelle che formano la cintura di Orione non sono allineate nello spazio, se si potessero unire con
una linea, questa sarebbe una spezzata, perché rispetto a un osservatore sulla terra sono a profondità
molto diverse tra loro, ma appaiono allineate perché i raggi visivi che le colgono stanno sullo stesso
piano e perché i raggi visivi non sanno "calcolare" la profondità dei punti visti. (Ricordiamo che la
visione diretta è "piatta" (vedi lez. 4 pg 12).
Possiamo definire in modo rigoroso quando più punti appaiono allineati:
Definizione di "apparente allineamento": Dati tre o più punti A,B,C,
e un punto O, questi
punti sono visti da O allineati se i raggi visivi OA, OB, OC,
giacciono su uno stesso piano.
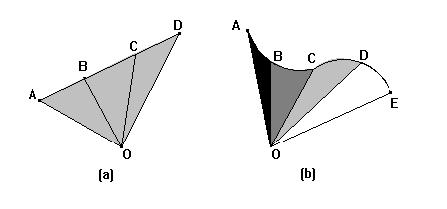
I raggi visivi in (a) sono complanari, per cui A,B,C,D sono visti allineati. Nel caso (b) invece i raggi visivi stanno su
piani diversi, per cui i punti A,B,C,D,E sono visti formare una linea curva
La definizione di "apparente allineamento" ci permette di affermare che:
Comunque si guardino tre punti allineati, questi vengono visti sempre allineati, un segmento appare
sempre rettilineo .
Questo fatto integra nel modello della geometria della visione il concetto di trasformazione e degli
elementi in essa invarianti, creando i primi importanti elementi concettuali per lo studio e la
comprensione della geometria proiettiva.
L'allineamento è; una proprietà invariante, che non dipende dal punto di vista. Il contrario non è;
vero:
Se tre punti si vedono allineati, non è; detto che lo siano anche nella realtà, cioè; non è detto che
giacciano realmente su una stessa retta.
-
La visione di segmenti paralleli
In Euclide l'idea di parallelismo è legata, come nel rinascimento, all'idea di equidistanza: la retta
parallela a una retta r è descritta da un punto P che si muove mantenendosi equidistante da r. In
quest'ambito dunque parallelismo ed equidistanza si equivalgono: una linea equidistante da una retta,
è una retta ed è parallela alla retta data, e viceversa.
La visione di segmenti o rette parallele viene affrontata nel:
Teorema 6 dell'Ottica: "Segmenti paralleli visti da lontano appaiono non paralleli"
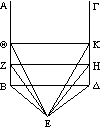
La dimostrazione che indica Euclide per il teorema 6 e molto importante perche il procedimento
seguito permette di ritrovare le prime tracce di quello che poi sara chiamato il punto di fuga. Euclide
infatti dimostra che due rette parallele non vengono viste equidistanti ma anzi si vedono convergenti,
poiche l'angolo visivo sotto il quale si vedono due punti equidistanti sulle due rette tende, come la
dimostrazione accerta, a zero.
Ecco la necessaria:
Definizione di "apparente convergenzah": Due rette parallele sono viste convergere a un punto se,
dato un qualunque angolo e, esiste un loro segmento di distanza che e visto sotto un angolo più
piccolo di e
Egli considera separatamente il caso in cui il punto di vista O sta sul piano delle due rette e il caso in
cui O sta su un piano diverso.
La dimostrazione, vista solo nel 1° caso, è essenzialmente identica a quella del teorema 5 e avviene
considerando il segmento AB di distanza tra le due parallele a e b e mostrando come questo,
allontanandosi dall'occhio, si veda progressivamente diminuire. Per questo i due segmenti non
appaiono equidistanti, ma anzi appaiono convergenti.
La circostanza che l'occhio si trovi all'interno della striscia, non è, come per il teorema 5, necessaria
alla nostra dimostrazione. Il teorema vale in ogni caso purché si aggiunga un'ipotesi, che molto
opportunamente Euclide formula esplicitamente aggiungendo "visti da lontano", l'ipotesi cioè che il
segmento di distanza AB sia abbastanza lontano dall'occhio. Qualunque sia la posizione dell'occhio,
dentro o fuori la striscia compresa tra le due parallele, da un certo punto in poi, l'angolo con cui si
vede il segmento di distanza AB diventa sempre più piccolo.
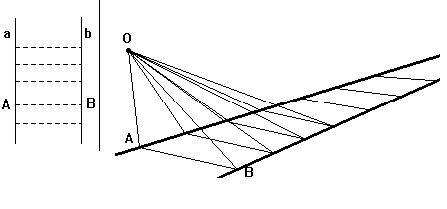
L
'animazione (Animazione V-1) che abbiamo realizzato permette di vedere come cambia l'angolo
visivo mano a mano che il segmento di distanza AB si allontana dall'occhio. Notiamo che, quando
l'occhio è fuori dalla striscia compresa tra le due rette parallele, l'angolo può anche aumentare
inizialmente, ma, da un certo punto in poi, che può essere determinato con precisione, comincerà a
decrescere tendendo a zero.
Il teorema viene simulato al prospettimetro, sul quale di possono misurare direttamente gli angoli
sottesi dai segmenti di distanza tra due rette parallele, ed è dimostrato successivamente in maniera
rigorosa, con l'appoggio di software di geometria dinamica. Si può darne infine una formulazione
moderna, nell'enunciato seguente:
Teorema della convergenza dei segmenti paralleli Segmenti paralleli, da un certo punto in poi,
si vedono convergere a uno stesso punto.
-
Il punto all'infinito, il punto di fuga
Il contesto appena affrontato, ha in qualche modo rafforzato nell'intuizione il concetto di limite, già
costruito in parte nella lezione 4, concetto estraneo alla preparazione degli studenti, ma
indispensabile per il proseguimento della trattazione, anche se non formalizzato.
Sempre col prospettimetro, si fa ancora notare come raggi visivi che colgono una retta, nel piano di
terra, ad esempio, salgono al raggio sul piano dell'orizzonte (raggio di fuga) parallelo alla retta di
terra, e contemporaneamente "ruotano" verso destra o verso sinistra, a seconda dei casi (vedi lez.4),
tendendo alla sovrapposizione col proprio raggio di fuga.

Il "salire" e il "ruotare" dei raggi visivi al loro raggio di fuga, nel percorrere una retta sul piano di terra,
inclinata a 45° rispetto alla linea di terra
Dopo qualche esempio pratico viene aggiunto al prospettimetro una cornice vuota, a una distanza
fissa dall'occhio, annunciando il passaggio dalla visione diretta a quella prospettica.
La cornice vuota permette il passaggio dei raggi (fili) visivi ma anche l'individuazione di una
virtuale superficie piana da essa contenuta, e la possibile individuazione della intersezione dei raggi
visivi con essa. I punti di intersezione saranno segnati sui fili con un pennarello.
Ecco una breve rassegna fotografica di alcuni momenti delle operazioni:

Si richiama l'attenzione alla posizione dell'occhio, all'altezza e alla sua distanza dalla cornice.

Si posiziona il foglio con i segmenti longitudinali e si fissano i "raggi" visivi

Usando la cornice e la riga si segnano i punti di intersezione col vetro virtuale dei raggi visivi che colgono i segmenti
longitudinali. è stato segnato anche il punto di fuga principale, qui non visibile.
FOTO CON RAGAZZI
Alcune studentesse, discutendo tra loro, mimano l'andamento delle rette parallele al raggio principale e il tendere ad
esso dei raggi visivi che corrono su tali rette

vista di profilo della situazione
Il tendere dei raggi visivi al raggio principale e il corrispondente tendere al punto principale dei
punti proiettati sul piano della cornice, rende plausibile la domanda: cosa corrisponde al punto
principale? le rette euclidee sono infinite solo potenzialmente, cioè sono prolungabili a piacere: dato
un punto lontano a piacere posso trovarne uno ancora più lontano, e proprio questa proprietà rende
impossibile determinare in esse un "punto all'infinito". Dagli studenti che osservano la situazione
sul prospettimetro viene fuori inoltre quanto segue: il raggio visivo che percorre una retta, più si
allontana dall'occhio più tende a sovrapporsi al raggio principale, qualunque sia la retta del fascio,
il raggio principale quindi, vista la corrispondenza uno a uno tra raggi visivi e punti in un piano,
dovrebbe cogliere un elemento infinitamente lontano comune a ogni retta, se esistesse. Proponiamo
di aggiungere questo astratto elemento comune a un fascio di rette parallele al piano euclideo,
creando in tal modo un oggetto matematico diverso, il piano proiettivo, che può portare interessanti
e feconde informazioni sulla trasformazione visiva, diretta e inversa. Questo astratto elemento
comune prende il nome di punto all'infinito, per rimanere nella trasformazione puntuale, e indica
ciò che hanno di comune tra loro rette parallele: la direzione.
Ogni fascio di rette, parallele tra loro, avendo una propria direzione, ha quindi un proprio punto
all'infinito, che viene colto dal raggio visivo con la stessa direzione. Si può allora pensare al piano
proiettivo come contenente anche una retta all'infinito, insieme di tutte le direzioni.
Si arriva, riassumendo la situazione, alle seguenti definizioni:
Punto all'infinito di un fascio di rette parallele: elemento comune a tutte le rette del fascio.
Punto di fuga di un fascio di rette parallele: punto corrispondente sul piano del quadro del punto
all'infinito di tali rette
Punto di fuga principale: punto corrispondente sul piano del quadro del punto all'infinito di un
fascio di rette longitudinali (parallele al piano di profondità e al piano di terra)
Si osserva infine come le direzioni di tutti i fasci di rette parallele contenuti in piani paralleli al
piano di terra si proiettano in una linea sul quadro, anch'essa parallela alla linea di terra, contenente
il punto di fuga principale. Tale linea si chiama linea dell'orizzonte.
Per esercizio si propone di individuare il punto di fuga di un fascio di rette inclinate a 45° sul piano
di terra, con l'aiuto del prospettimetro. Con semplici considerazioni sulle proprietà del triangolo
rettangolo con angoli a 45° si arriva a stabilire che il punto cercato si trova sulla linea
dell'orizzonte, distante dal punto centrico quanto l'occhio dal piano del quadro. Questo punto di
fuga particolare prende il nome di punto di distanza.
Con la proiezione di dipinti scelti opportunamente si può confrontare la visione diretta con
rappresentazione prospettica e si possono individuare sul piano del dipinto gli elementi definiti
nell'attività di laboratorio.
Analizziamo da un punto di vista prospettico un dipinto di Duccio da Buoninsegna datato 1308
(fig. 4) e l'affresco della Stanza delle Maschere (fig. 5), trovato a Roma nel 1961 e datato 38 a.C.

Fig.4

Fig.5
Nel quadro di Duccio, i segmenti che rappresentano la travatura del solaio presumibilmente
rappresentano segmenti paralleli. Se prolungati (fig. 6), si vedono incontrarsi in vari punti, non si
vedono cioè convergere a uno stesso punto. La distribuzione dei raggi visivi che si produce
guardando il quadro non coincide dunque con quella che si otterrebbe guardando a 4 segmenti
orizzontali paralleli tra loro posti sopra il piano orizzontale.

Fig.6
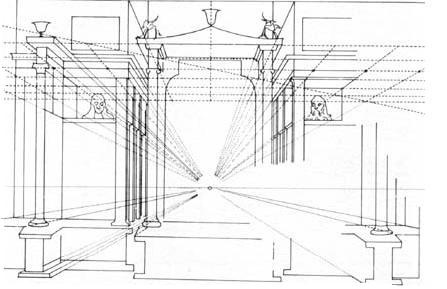
Fig.7
Se analizziamo invece la stanza delle maschere (fig. 7) vediamo come tutti i segmenti paralleli
all'asse del cono visivo siano disegnati convergenti al punto principale coerentemente col teorema 6
In un altro dipinto di Duccio da Buoninsegna, "L'ultima cena", (fig. 8) gli spigoli laterali del tavolo
sembrano all'occhio dell'osservatore contrari a come dovrebbero apparire e le linee del soffitto, che si
suppone squadrato con segmenti paralleli, non sono rappresentate coerentemente col teorema 6 di
Euclide (fig. 9)

Fig.8

Fig.9
Ad un approccio empirico come è quello dei pittori medioevali, si contrappone nel Rinascimento
una ricerca geometrica fondata sui principi della geometria della visione che tenda a dare alla
prospettiva lo statuto di scienza. Se, ad esempio, analizziamo l' "Ultima cena" di Andrea del
Castagno, contemporaneo di Leon Battista Alberti (fig. 10), notiamo un impianto prospettico nel
quale le linee di profondità, parallele tra loro, sono correttamente rappresentate con linee
convergenti verso quello che Alberti chiamerà il "punto centrico", cioè il punto di fuga principale
(fig. 11). In questa analisi grafica si può notare anche un punto di fuga non appartenente alla linea
dell'orizzonte, al quale convergono le linee formate dalle tegole del tetto, non parallelo al piano di
terra ma inclinato rispetto ad esso. Questo punto di fuga non appartiene al dipinto ma è stato
accuratamente utilizzato dal pittore.

Fig.10

Fig.11