PROSPETTIMETRO

Il prospettimetro è uno strumento ideato dalla prof. Laura Catastini.
In legno e plexiglas, è formato da tre piani: uno fisso in legno (piano di terra su cui possono essere disposti dei fogli per scrittura) e due in plexiglas rimovibili: il piano dell"orizzonte parallelo al piano di terra e il piano di profondità ad essi perpendicolare. Un chiodo al quale sono fissati dei fili colorati simula il punto di vista e i fili i raggi visivi.
Lo strumento è corredato da supporto verticale in plexiglas formato da due rettangoli alti e stretti uniti lungo il lato maggiore a formare un angolo retto, in modo da fornire un appoggio a cui fissare i fili che colgono punti dello spazio che non stanno sul piano di terra o sul piano dell"orizzonte. Il supporto verticale è rimovibile e posizionabile a piacere.
Il nome "prospettimetro" deriva dalla possibilità di effettuare misurazioni nell"ambito della "perspectiva naturalis", come veniva chiamata la visione diretta fino al quattrocento, epoca nella quale viene messa a punto la "perspectiva lineare", tecnica di rappresentazione pittorica il cui strumento principe sarà il prospettografo (è lo strumento che permette di disegnare su un piano di vetro oggetti che stanno dietro il piano, traguardati da un mirino fisso, con un solo occhio). Il semplice termine "prospettiva", in uso anche oggi, indica la "prospettiva lineare.

Foto 1: Prospettimetro e supporto verticale sul quale è stato disegnato il punto A e il cui piano di terra è stato rivestito con un foglio di carta per poter tracciare linee

Il piano di profondità, in questo primo prototipo, si ferma sotto il piano dell"orizzonte per semplificare la costruzione dello strumento, ma non impedisce una agevole attività di laboratorio.

Foto 2: Prospettimetro e supporto verticale al quale è stato fissato un filo che coglie il punto A e che simula il raggio visivo uscente dall"occhio posto nella posizione del chiodo al quale è legato il capo fisso del filo.

L'uso del prospettimetro permette una simulazione dinamica nello spazio che "educa" e potenzia scientificamente il pensiero immaginativo nel senso che fornisce ricche descrizioni multisensoriali di oggetti matematici e le tante relazioni concrete tra essi. Le forme (Gestalt) prodotte da questa attività sono il motore di quello che Wertheimer chiama "ricentramento cognitivo". Il ricentramento cognitivo si attua ogni volta che in un quadro concettuale si intravedono nuove relazioni tra gli elementi costitutivi del quadro che ne fanno emergere nuova conoscenza rispetto a quella iniziale. Questo movimento di pensiero viene chiamato da Wertheimer "pensiero produttivo". I ricentramenti cognitivi e il pensiero produttivo sono agevolati dalla percezione dinamica della situazione concreta che si sta analizzando. L"educazione scientifica del pensiero immaginativo consiste nella continua verifica della corrispondenza rigorosa tra modelli e gestalt che si costruiscono con il pensiero e le relazioni formali della teoria matematica all"interno delle quale si svolge il lavoro. Spesso negli studenti la modellizzazione, che avviene in modo spontaneo e di norma non seguita dall"insegnante, si ferma a uno stadio iniziale perché contiene errori che la rendono presto inservibile¹. Si perde così un importante strumento di pensiero, prezioso perché instaura flessibilità ideativa, creatività scientifica e una intensa partecipazione emotiva che motiva positivamente al lavoro.

SVOLGIMENTO LABORATORIO

• Più a destra, più a sinistra

Sono stati presentati in proiezione i teoremi 10,11,12 dell"Ottica, che descrivono il modo in cui, sotto determinate ipotesi, è visto un segmento posto longitudinalmente e come questo, andando in profondità, sembri spostarsi verso l"alto o verso il basso, o deviare a destra o a sinistra. (Diciamo che un segmento AB è posto longitudinalmente se non si trova su un piano perpendicolare al raggio principale, nozione questa che può essere didatticamente illustrata con il prospettimetro.)

Cliccando l"icona 1 è possibile illustrare i vari enunciati (vedi Animazione IV-1).

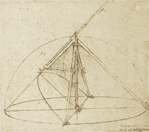
1 - Miniatura da una edizione manoscritta del 1458 dell'Ottica di Euclide

Teorema 10: Tra i piani che giacciono sotto l'occhio quelli [più] lontani appaiono più in alto.
Teorema 11: Tra i piani che stanno sopra l'occhio i [più] lontani appaiono più in basso.
Teorema 12: Tra i [segmenti] che si estendono longitudinalmente, quelli a destra sembrano deviare verso sinistra, quelli a sinistra verso destra.

In questi teoremi, dei quali abbiamo riportato il testo originale, si leggono le espressioni "apparire più alto, più basso, più a destra, più a sinistra" che trovano definizione nelle premesse V e VI dell"Ottica, che regolano l"apparente posizione relativa delle cose viste. In questi assiomi si dice che la posizione apparente delle cose dipende dalla posizione del raggio visivo che le coglie: ad esempio, se una cosa A è colta da raggi visivi più in alto o più a destra di quelli che colgono una cosa B, allora A apparirà più in alto o più a destra di B. Non è data la nozione di raggio più alto, più basso, più a destra o più a sinistra, che resta così intuitiva. Abbiamo perciò proposto, prima di vedere le dimostrazioni, di determinare insieme le definizioni mancanti, come abbiamo fatto nel caso della distanza di un punto da un segmento, sottolineando l"assoluta necessità del definire ciò che si usa, di non lasciare nulla di approssimativamente intuitivo, pena il crollo della certezza logica del nostro sistema assiomatico.

Gli studenti cominciano a cercare una definizione di "essere più a destra, più a sinistra", per quanto riguarda due punti, ma nessuno riesce a darne una soddisfacente. La ricerca però li rende immediatamente consapevoli della necessità di riferimenti. Si mostra il cono visivo e si individuano piani e assi di riferimento "naturali" legati all'osservatore

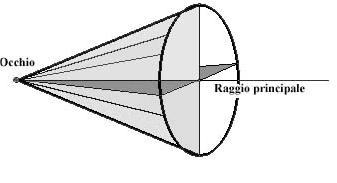
Fig 1: cono visivo, asse del cono, coppia di piani perpendicolari contenenti il vertice e l'asse.

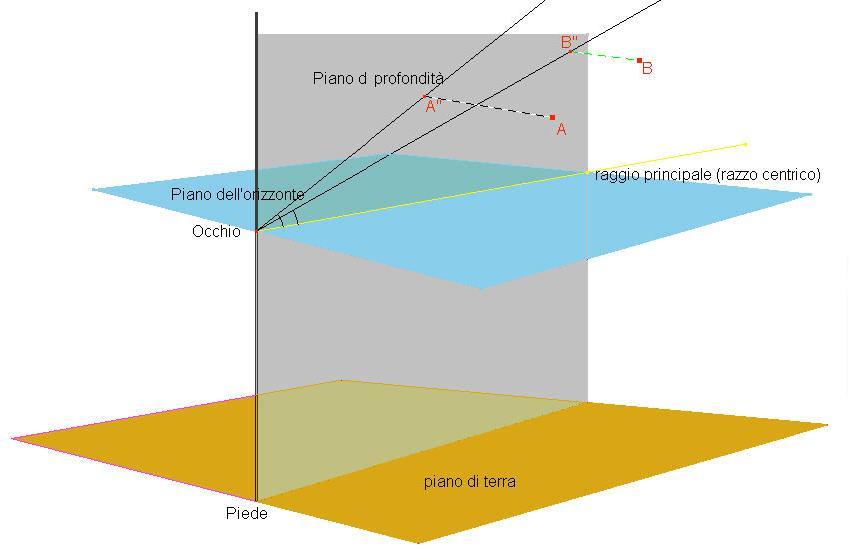
Nello spazio vengono individuati:
il piano di terra: piano orizzontale perpendicolare nel piede all"asse occhio-piede dell'osservatore
il piano dell'orizzonte: piano contenente l'occhio parallelo al piano di terra,
il piano di profondità: piano contenente l"asse occhio-piede e il raggio principale, perpendicolare al piano di terra e al piano dell'orizzonte.
la linea di terra: retta passante per P (piede) perpendicolare alla proiezione sul piano di terra del raggio principale.
Ricordiamo che ogni retta definisce una direzione e che rette parallele hanno la stessa direzione. Definiamo sulla linea di terra un verso "a destra" rispetto a P e di conseguenza anche un verso "a sinistra". Concordiamo di usare il verso naturale. Il piano di profondità determina quindi due semispazi, uno destro e uno sinistro.

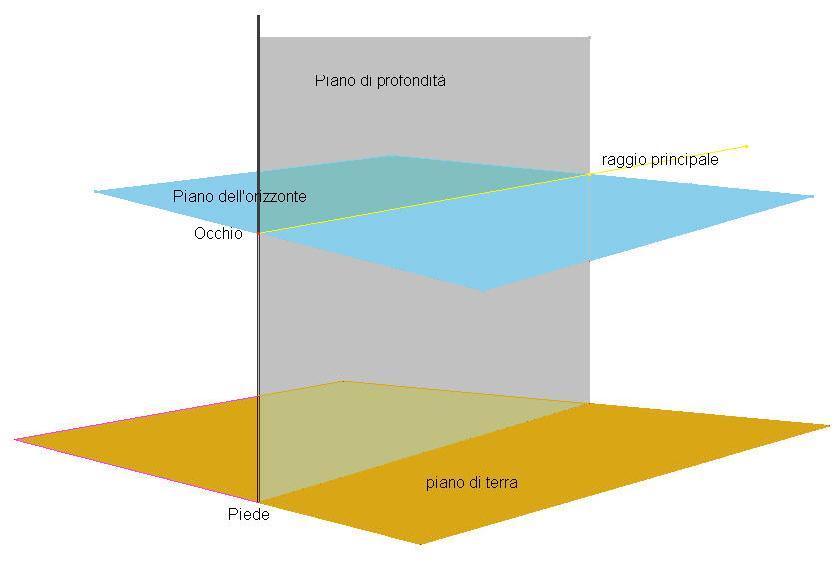
Fig. 2: piani individuati nello spazio tra cui scegliere i possibili piani di riferimento

La scelta e la messa a punto delle definizioni vengono fatte usando il prospettimetro, mediante il quale è possibile simulare la posizione dei punti nello spazio, l"incidenza dei raggi visivi sui punti osservati e la misurazione di segmenti o degli angoli che un raggio visivo, o una sua proiezione particolare, forma con altri elementi dello strumento, come ad esempio il raggio principale 5 Si chiede, nel caso particolare mostrato nella foto 3, di determinare quale punto è più a destra o più a sinistra

FOTO CON RAGAZZI

Foto 3: discussione tra studenti su come stabilire quale dei punti A e B sia più a destra rispetto all"occhio

Vengono così determinate con gli studenti le due definizioni di "essere più a destra o più a sinistra" che ci interessano:
Definizione di "essere più a destra o più a sinistra" di punti nello spazio (rispetto al piano di profondità): dati due punti A e B nel semispazio di destra, diremo più a destra quello la cui distanza – AA', BB' – dal piano di profondità è maggiore, più a sinistra quello la cui distanza è minore. Viceversa se i punti si trovano nel semispazio di sinistra.

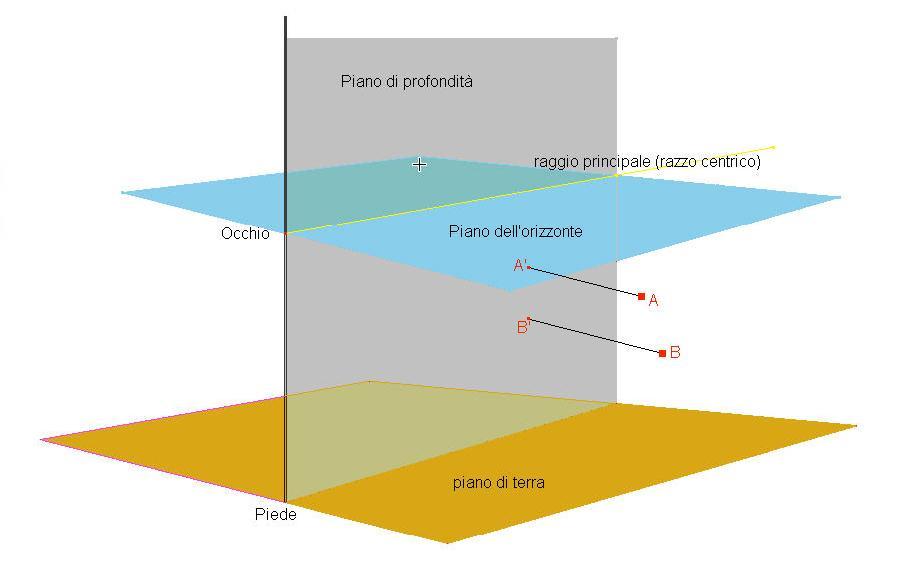
Fig.3

Si potrebbe in questa situazione far notare come questa doppia definizione, spezzata in due dal luogo di collocazione dei punti, potrebbe essere unificata nel momento in cui fossero usate delle coordinate nello spazio. L'introduzione infatti di un sistema di coordinate il cui asse delle ascisse fosse la linea per l"occhio parallela alla linea di terra, permetterebbe di sostituire la misura dei segmenti AA", BB" con le ascisse di A e di B, e renderebbe possibile una sola, agevole, definizione: dati due punti A e B nello spazio diremo più a destra quello la cui ascissa è maggiore, più a sinistra quello la cui ascissa è minore.
Definizione di "essere più a destra o più a sinistra" di raggi visivi nello spazio (ispetto al piano di profondità): dati i raggi visivi OA e OB a destra del piano di profondità, considerate le loro proiezioni OA" e OB" sul piano dell"orizzonte, e gli angoli O"OA". O"OB" che esse formano con il raggio principale, diremo che è più a destra il raggio visivo che forma con il raggio principale l"angolo più grande. Analogamente se i raggi si trovano a sinistra del piano di profondità.

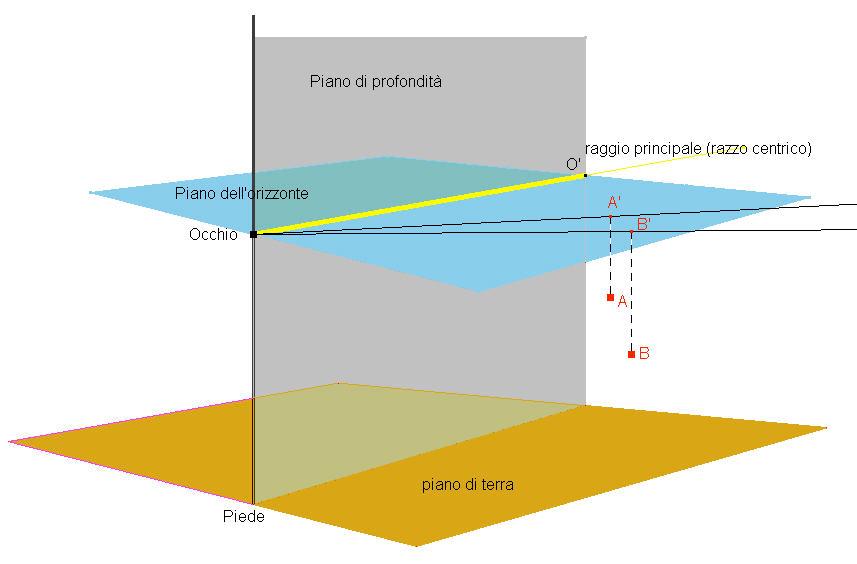
Vedere più a destra, più a sinistra
Come definire invece il "vedere più a destra o più a sinistra"? Date le premesse V e VI che legano la posizione apparente di un punto alla posizione del raggio visivo che lo coglie:
V – E che le cose viste sotto raggi più alti appaiano più in alto, quelle [viste] sotto [raggi] più bassi più in basso
VI – E allo stesso modo che le cose viste sotto raggi più a destra appaiano più a destra, quelle [viste] sotto [raggi] più a sinistra appaiano più a sinistra è immediato stabilire la
Definizione di "vedere più a destra o più a sinistra": dati due punti A e B nel semispazio destro, colti dai raggi visivi OA e OB, si vede più a destra il punto il cui raggio visivo corrispondente è più a destra. Viceversa se i punti si trovano nel semispazio sinistro.

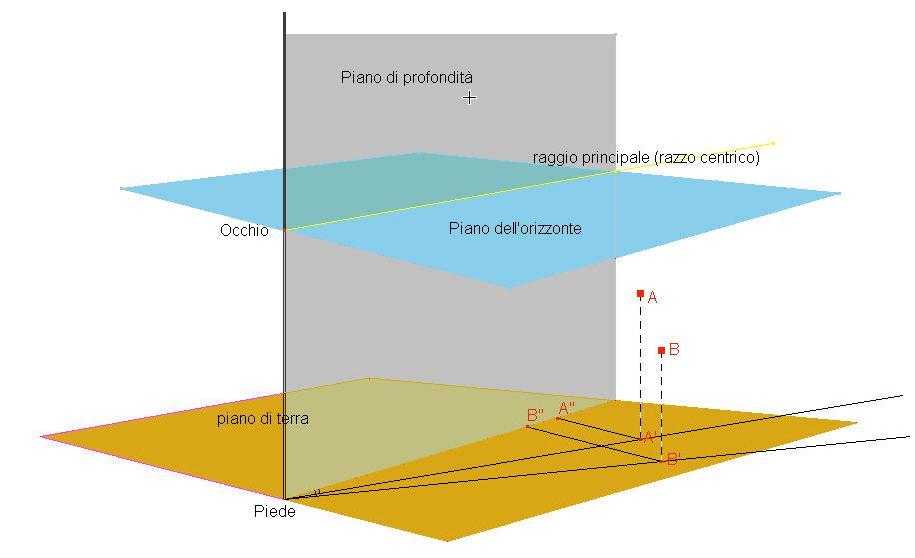
Fig.4

Nel caso dell"uso reale del prospettimetro che permette di fare le misure necessarie, proietteremo per comodità sul piano di terra invece che sul piano dell"orizzonte (vedi figura sotto) data l"uguaglianza degli angoli garantita dal parallelismo tra i due piani.

Fig.5

Usando solo riga e squadra e volendo conoscere la misura degli angoli in questione, come fare? Gli studenti questa volta, (vedi Lab. II) non hanno difficoltà a misurare i cateti degli angoli rettangoli 8 che si formano e a costruire i rapporti giusti per determinare le tangenti degli angoli interessati (uso della tavola delle tangenti).

Foto: procedimento di misura di quanti gradi si vede a destra il punto A

Anche in questo caso, e in tutti gli altri che seguono, si potrebbero unificare i due casi della definizione introducendo angoli con segno. La scelta sul prospettimetro del sistema di riferimento e la ricerca grafica delle coordinate crea un modello spaziale forte che può supportare in seguito, anche in ambito universitario, lo sviluppo della geometria analitica nello spazio tridimensionale affiancando gli algoritmi di calcolo con la concettualizzazione spaziale degli oggetti sottesi al simbolismo algebrico, concettualizzazione che sembra drammaticamente mancare oggi negli studenti universitari.

L'attività prosegue con le misurazioni e le conclusioni in casi concreti presentati sul prospettimetro, tra le quali, molto importante, si verifica che punti del semipiano destro di terra che sono egualmente a destra del piano di profondità (appartenenti cioè a segmenti di longitudinali profondità, cioè perpendicolari alla linea di terra), si vedono progressivamente più a sinistra se sono più lontani poiché l"angolo che li definisce diminuisce.

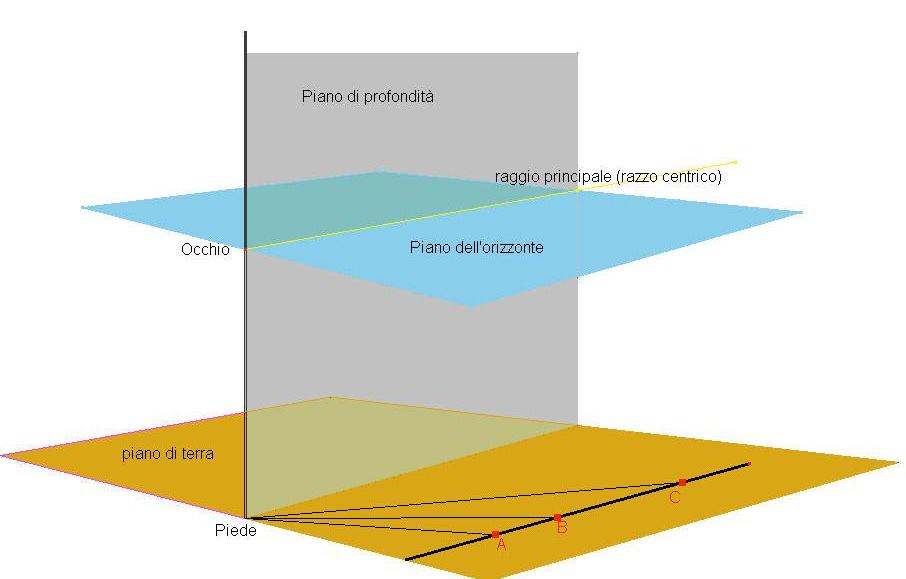
Fig.5

Foto: procedimento di misura di quanti gradi si vede a destra il punto A

• Più alto, più basso

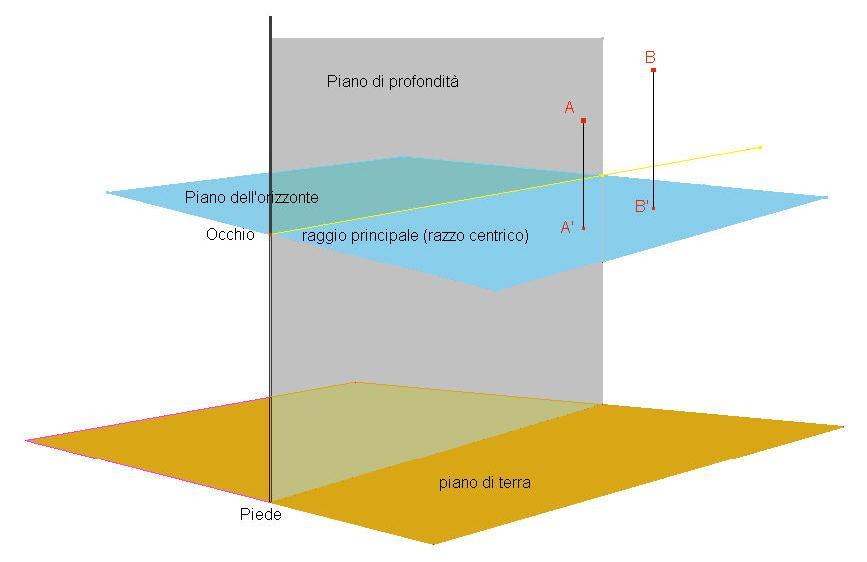
Definizione di "essere più in alto o più in basso" di raggi visivi nello spazio (rispetto al piano dell"orizzonte): dati i raggi visivi OA e OB sopra il piano dell"orizzonte, considerate le loro proiezioni OA' e OB' sul piano di profondità, e gli angoli O'OA'. O"OB" che esse formano con il raggio principale, diremo che è più in alto il raggio la cui proiezione forma con il raggio principale l'angolo più grande. Analogamente se i raggi si trovano a sinistra del piano di profondità.

Vedere più alto o più basso

Definizione di vedere più alto o più basso di due punti (rispetto al piano dell'orizzonte): dati due punti A e B sopra il piano dell"orizzonte, colti dai raggi visivi OA e OB, si vede più in alto il punto il cui raggio visivo corrispondente è più in alto. Viceversa se i punti si trovano sotto il piano dell'orizzonte.

NON C'E'

è stato sottolineato col prospettimetro come dato un singolo raggio visivo, tutti i punti colti nello spazio dal raggio si vedono ugualmente rispetto all"alto, basso, destra o sinistra, con la semplice osservazione che la proiezione del raggio visivo è la medesima per ogni punto.

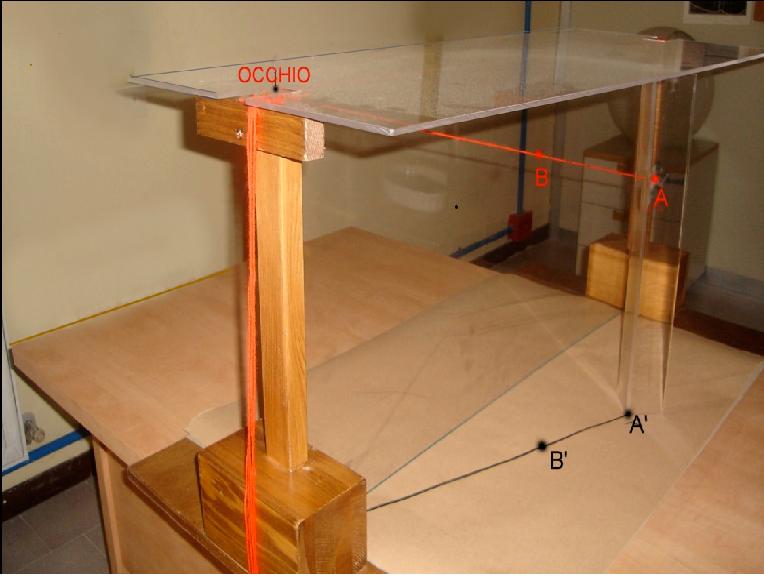
Foto: i punti A e B che sono colti dallo stesso raggio visivo stanno entrambi sulla proiezione del raggio sul piano di terra e sono quindi visti ugualmente rispetto alla destra e alla sinistra.

Questo porta alla equivalenza visiva tra i punti che appartengono a un singolo raggio visivo. Da un punto di vista geometrico, senza indizi psicologici di distanza, tutti questi punti appaiono il medesimo e non si distinguono l'uno dall'altro rispetto alla loro posizione per esempio in profondità, dando la stessa impressione visiva.
Quest'ultima osservazione è molto importante nel passaggio dalla visione diretta alla rappresentazione prospettica (e alla geometria proiettiva).
Viene presentata la Tavola IV-1 (soluzione nella Tavola IV-5)

TAVOLA IV-1 La foto seguente permette di stabilire se la palla è già in rete o ne è ancora fuori? Motiva la risposta alla luce degli argomenti appena trattati

• Dimostrazione dei teoremi 10, 11 e 12

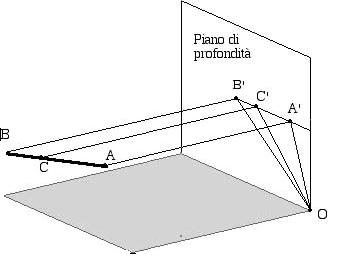
Ipotesi: AB è parallelo al piano dell'orizzonte, AB è posto sopra il piano dell'orizzonte, AB è posto longitudinalmente davanti all"occhio
Tesi: un punto C del segmento AB che si allontana dall"occhio è visto abbassarsi.

Dimostrazione Dato cha AB è posto longitudinalmente rispetto all'occhio la sua proiezione ortogonale sul piano di profondità non può essere un punto. Sarà dunque un segmento A'B'.

Dato che il segmento AB è parallelo al piano dell'orizzonte anche la sua proiezione, il segmento A'B' sarà parallela a tale piano e quindi sarà parallela all'asse del cono visivo.

Sul piano di profondità la situazione si presenta esattamente come nella figura dell'Ottica di Euclide

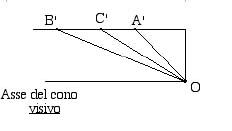
L"angolo che forma C"O con l'asse del cono visivo diventa sempre più piccolo man mano che C si avvicina a B, per il Teorema del punto interno (vedi schede dei preliminari). Ciò significa, per la definizione del "vedere più basso" che il punto C è visto abbassarsi.

C. V. D

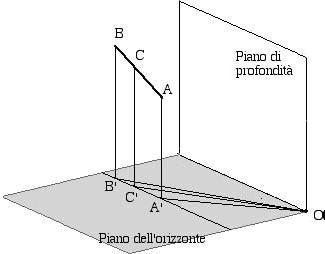
TEOREMA 12   Un qualunque segmento AB parallelo al piano di profondità e posto longitudinalmente ² davanti all"occhio, se si trova a sinistra del piano di profondità è visto deviare verso destra, se si trova a destra è visto deviare verso sinistra.

La dimostrazione di questo teorema è del tutto simile alla precedente e per questo ne riportiamo solo le ipotesi, la tesi e la figura che ne illustra il significato.
Ipotesi: AB è parallelo al piano di profondità, AB è posto a sinistra il piano di profondità, AB è posto longitudinalmente davanti all'occhio.
Tesi: un punto C del segmento AB che si allontana dall"occhio è visto deviare verso destra.

² Ricordiamo che un segmento AB è posto longitudinalmente se non si trova su un piano perpendicolare al raggio principale.

Osserviamo che, se immaginiamo di prolungare il segmento AB (posto ad esempio a sinistra del piano di profondità), allontanando progressivamente B dall"occhio, esso ci apparirà deviare progressivamente verso destra avvicinandosi sempre più al piano di profondità senza mai toccarlo. Anche in questo caso, come nei casi precedenti, tutto ciò può essere formalizzato usando il linguaggio dei limiti.

Osserviamo infine che i punti di un segmento verticale parallelo al piano di profondità non deviano né a destra né a sinistra, infatti questi punti si proiettano sul piano dell"orizzonte in uno stesso punto. Lo stesso accade per i punti di un segmento orizzontale perpendicolare al piano di profondità: esso sarà visto come un segmento orizzontale senza alcuna deviazione né verso l"alto né verso il basso.

• L'essere e le coordinate nello spazio:

Si riassumono e considerazioni fatte fino a questo punto con il confronto tra la rappresentazione mediante coordinate nello spazio della posizione (l"essere) di un punto in termini di "destrasinistra", "alto-basso", "davanti-dietro" e quella della visione di un punto nello spazio (l'apparire) negli stessi termini:

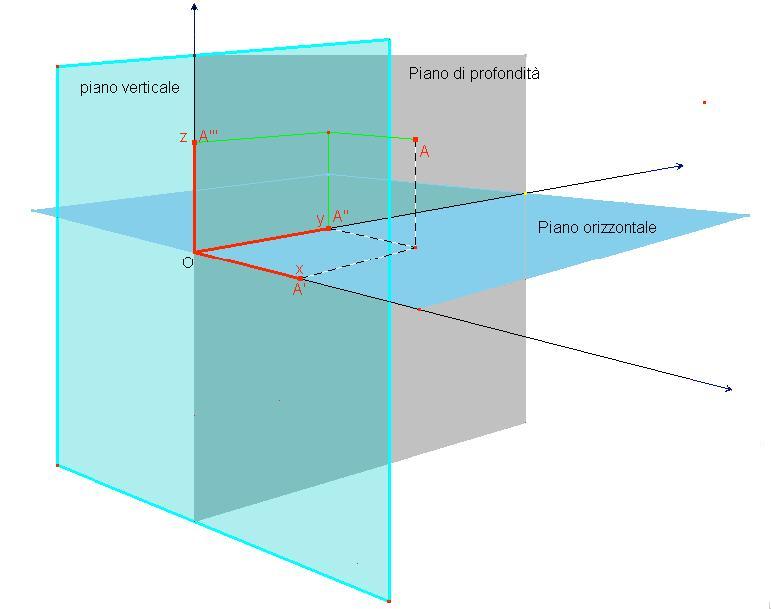
Fig. 6 Riferimento cartesiano scelto con l'origine nell'occhio, l'asse y coincidente con il raggio principale e l'asse z con l'asse occhio-piede dell'osservatore

Per chiarezza di immagine abbiamo evidenziato solo i semiassi positivi (destra, davanti, alto) e solo il semispazio "davanti" definito dal piano verticale.
Le coordinate sulla retta intersezione tra il piano orizzontale e quello verticale danno il destrasinistra, quelle sulla retta intersezione tra il piano verticale e quello di profondità danno l"alto-basso, quelle tra il piano di profondità e il piano orizzontale l'avanti-dietro. Conviene far verbalizzare agli studenti questa descrizione che individua gli assi coordinati.

• L'apparire e gli angoli direttori

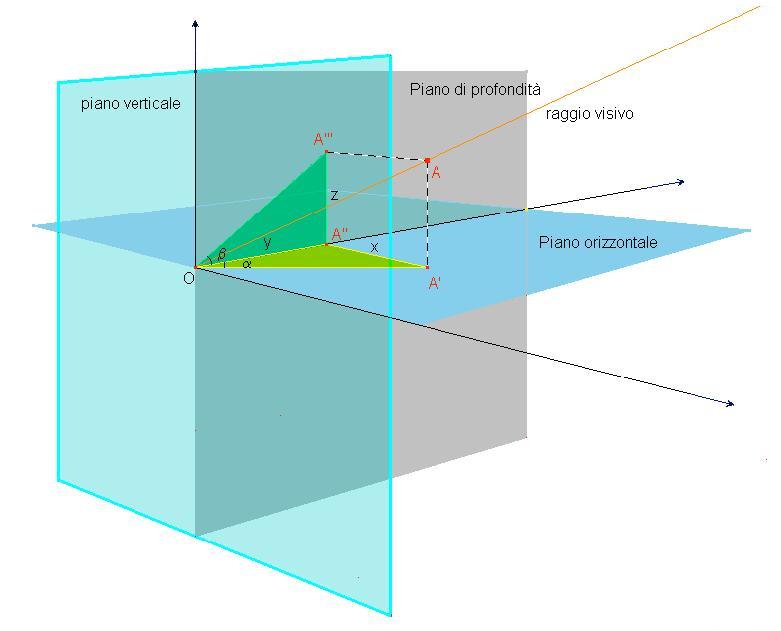
Fig. 7 - Gli angoli direttori

La misura dell'angolo α formato dallfasse OA" con la retta OA', proiezione sul piano dell'orizzonte del raggio visivo che coglie il punto A, esprime quanto a destra appare il punto rispetto al piano di profondità.
La misura dell'angolo³ β formato dallfasse OA" con la retta OA''', proiezione sul piano di profondità del raggio visivo che coglie il punto A, esprime quanto alto appare il punto rispetto al piano dell'orizzonte.

Viene presentata la Tavola IV-2 (soluzioni Tavola IV-5)

Il teorema 12 puo riformularsi usando il linguaggio dei limiti, dicendo che se A si trova su una retta longitudinale parallela al piano verticale e α e il suo angolo direttore allora α tende a 0 se A si allontana infinitamente dall'occhio. Analogamente il teorema 10, 11: se un punto A si trova su una retta longitudinale parallela al piano dell'orizzonte e β è il suo angolo direttore, allora allontanandosi infinitamente A dall'occhio l'angolo β tende a 0.

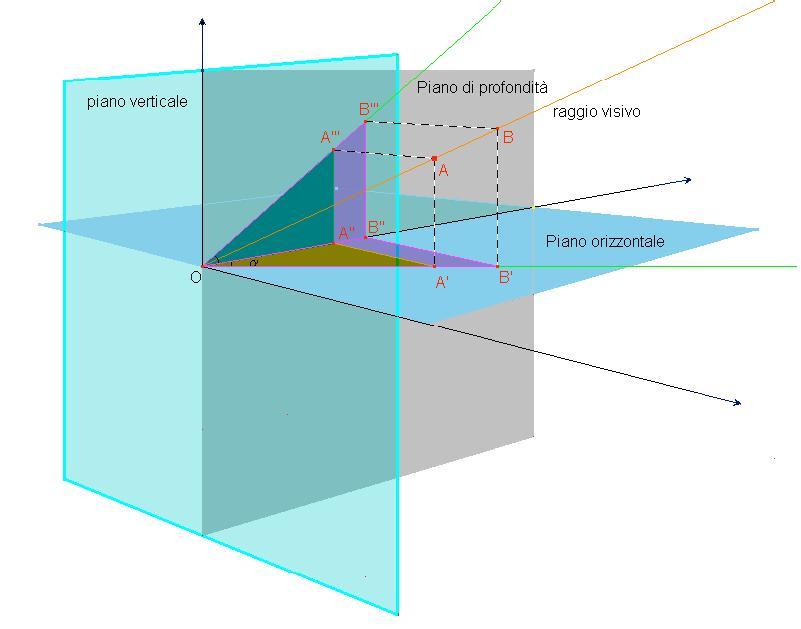
Fig 8 - I piani dell'apparire

Sottolineiamo ancora come nella visione non abbia senso il "più indietro" e il "più avanti" di un punto colto da un raggio visivo rispetto a un altro punto colto dallo stesso raggio, dato che gli angoli sottesi rimangono gli stessi, rendendo tutti i punti di un raggio visti ugualmente.
A e B (fig. 8) sono individuati dalla stessa coppia di angoli, quindi sono "visti" ugualmente.

Non apparendo il "più avanti" e il "più indietro", la visione geometrica diretta si può senz"altro definire una visione "piatta" dello spazio.
Da un punto di vista percettivo la situazione è analoga: noi vediamo un ambiente tridimensionale non per la posizione dei punti nello spazio ma perché usiamo ulteriori indizi percettivi, quali il fatto che un corpo opaco nasconde le parti degli oggetti più lontani allineati con lui e con l"occhio, la conoscenza multisensoriale degli oggetti, l"illuminazione, le ombre, i colori, la densità dell"aria, la visione binoculare. In assenza di questi indizi percettivi la nostra visione risulta piatta e siamo incapaci di dire quale elemento è più vicino o più lontano dall"occhio. Pensiamo alle costellazioni che disegnano figure nel buio del cielo: data la lontananza mancano indizi prospettici e manca l"apparire più avanti o indietro delle stelle che così disegnano forme che appaiono all"occhio come su una tavola, complanari, anche se le stelle che le formano non lo sono.

Vengono presentate le Tavole IV-3 e IV- 4 (soluzioni nella tavola IV-5)

TAVOLA LABORATORIO IV-3 FLATLANDIA 1 Ecco come un abitante di Flatlandia4 descrive la geometria e la percezione della sua visione: "non siamo in grado di [ ] poter distinguere una Figura da un"altra [ ] tutte le Figure hanno l"aspetto di una Linea Retta.. noi gli angoli non possiamo vederli, possiamo però dedurli [a causa di una nebbia frequente nel paese ] Dovunque ci sia una buona dose di Nebbia, ecco che gli oggetti a una distanza, diciamo, di un metro, sono sensibilmente meno nitidi di quelli che si trovano a novantacinque centimetri" La spiegazione continua così: «se incontrassi due estranei, ad esempio un Triangolo Equilatero e un Pentagono, come farei a distinguerli? Se mi dispongo in modo che lo sguardo bisechi un angolo (A) del Triangolo, quello che vedrò di lui sarà un segmento DE il cui punto centrale sarà assai nitido, essendo il più vicino a me, ma andando verso gli estremi la linea sarà sempre meno nitida perché il lati AB e AC si perdono rapidamente nella nebbia. 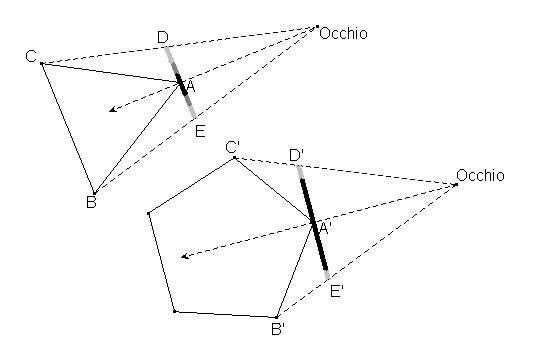Nel caso del Pentagono invece , benché continui a vedere un segmento D"E", non solo il centro A" sarà nitido ma anche gran parte della linea, perché i lati si perderanno meno rapidamente nella nebbia." Secondo voi: 1 L'autore espone solo un modello geometrico di visione diretta? 2 Possiamo dire che in Flatlandia la visione è "piatta" come nel nostro mondo? 3 Come viene visto in Flatlandia un semipiano davanti all"occhio di chi guarda? Come viene visto un quadrato? 4 Come viene vista una circonferenza in Flatlandia? 5 Come si vede una sfera nel nostro mondo? 4 E.A.Abbot, Flatlandia, Adelphi e la Nuova Italia, Perugia, 1995

TAVOLA IV-4 FLATLANDIA 2 Teoremi 10-11-12 dell"Ottica (sulla terra): Un qualunque segmento AB parallelo al piano dell"orizzonte e posto longitudinalmente 5 davanti all"occhio se si trova sopra il piano dell"orizzonte è visto deviare verso il basso, se si trova sotto è visto deviare verso l"alto. 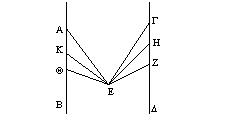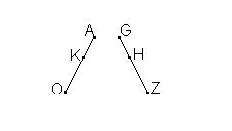Tra i [segmenti] che si estendono longitudinalmente, quelli a destra sembrano deviare verso sinistra, quelli a sinistra verso destra Come i segmenti sono nello spazio Come i segmenti si vedono nello spazio Come andrebbero formulati in Flatlandia gli analoghi dei Teoremi 10-11-12 dell'Ottica? Illustrare con un disegno: come si vedono i segmenti in Flatlandia nelle ipotesi del teorema 12? Come si vedono se c'è la Nebbia?

⁵ Ricordiamo che un segmento AB è posto longitudinalmente se non si trova su un piano perpendicolare al raggio principale.

Queste considerazioni evidenziano la distanza che sempre esiste tra il "modello matematico" e la situazione reale che il modello vuole interpretare. I due piani sono strettamente distinti e si deve evitare di sovrapporli: un conto è il modello, che necessariamente trascura una serie di fatti e un conto è la realtà che il modello vuole descrivere, generalmente molto più complessa. Senza fare chiarezza su questa distinzione, fondamentale nella matematica contemporanea, non si comprenderebbe come le stesse situazioni reali possano essere descritte da diversi modelli matematici e come il compito del matematico sia proprio quello di creare modelli coerenti in grado di interpretare i fenomeni per poter fare previsioni.

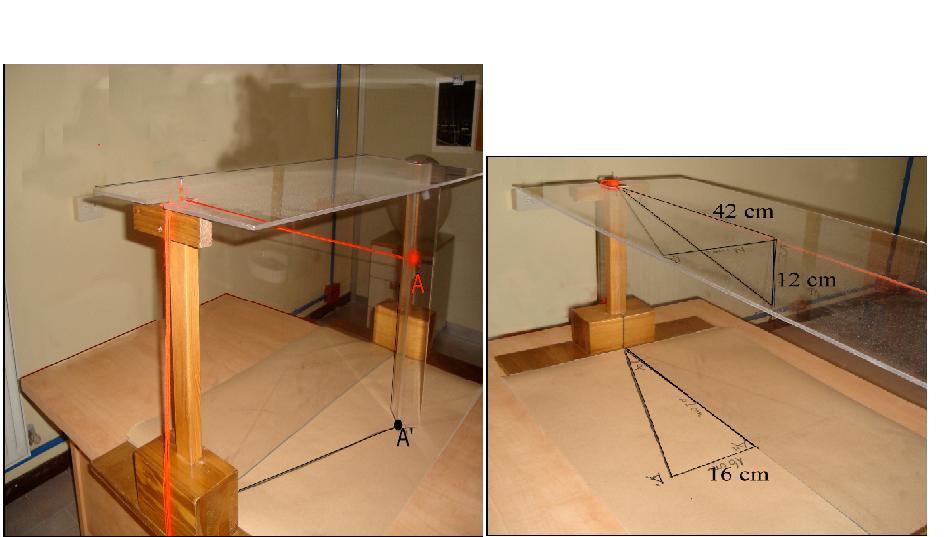
BREVE DOCUMENTAZIONE FOTOGRAFICA Si lavora con strumenti geometrici e pennarello su un foglio di carta che fodera il piano di terra, per proiettare i punti sul piano di profondità e individuare gli angoli. La tecnica si affina: come proiettare punti "sospesi"? Rimosso il sostegno verticale, si lavora con le proiezioni e le misure dei cateti per individuare le tangenti.