|
|
"Le geometrie della visione" Liceo Classico Varrone (Rieti) 2005-2006 APPENDICE NOTE |
|
|
Nota 1 Non possiamo pensare che l'arco di circonferenza sia il luogo geometrico dal quale si vede
ugualmente il segmento AB. La definizione di luogo geometrico infatti impone che l'insieme di
punti che lo costituisce non solo soddisfi nella sua totalità una proprietà data, in questo caso
l'equivisione, ma che anche esaurisca tutti i punti del piano che hanno tale proprietà. Questa ultima
condizione non è soddisfatta dai punti dell'arco, che non sono gli unici da cui si vede AB sotto il
medesimo angolo.
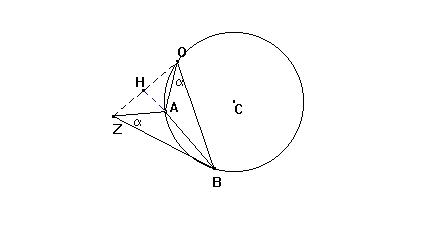
Fig.1 Il punto Z è stato ottenuto con una semplice costruzione: da un punto O dell'arco APB si traccia la perpendicolare ad AB e su tale perpendicolare si prende ZH = OH. Lasciamo per esercizio la dimostrazione che gli angoli in O e in Z che sottendono AB sono uguali.Se pensiamo di fare questa operazione per ogni punto del l'arco (in pratica stiamo eseguendo una simmetria assiale di asse AB), otteniamo questo insieme L di punti.
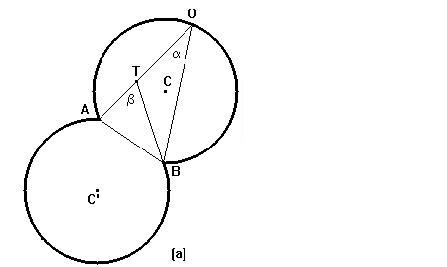
Fig.2 L'insieme dei punti L così realizzato è un luogo geometrico: è il luogo dei punti dai quali il segmento AB viene visto sotto lo stesso angolo.La dimostrazione di quanto affermato è semplice: abbiamo appena visto che tutti i punti del luogo soddisfano la proprietà richiesta, ci resta da provare che solo loro hanno tale proprietà. Questo è vero per il seguente teorema: IV. TEOREMA Se T è un qualunque punto interno all'insieme L allora il segmento AB viene visto da T più grande che da un qualunque punto di L, se T è invece è esterno il segmento AB viene visto più piccolo Ipotesi: T è interno a L Tesi: ATB > AOB Dimostrazione Sia T interno a L. Sia O sul prolungamento di AT. L'angolo ATB, poiché esterno al triangolo BTO è più grande dell'angolo AOB quindi AB si vede più grande dal punto T che dal punto O.
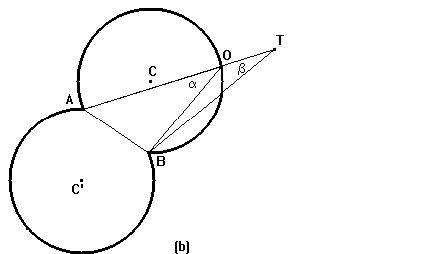
Fig.3 Se T è esterno a L si può procedere nello stesso modo come chiaramente mostrato dalla figura BC.V.D. Il teorema che abbiamo dimostrato ci permette di risolvere definitivamente il seguente problema: dato un segmento AB e due punti O e O' da quale posizione la grandezza AB è vista più grande? |