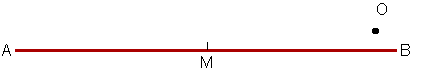Scheda didattica

Laura Catastini

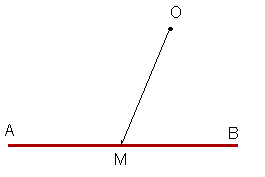
La distanza tra due punti è la lunghezza, rispetto a una fissata unità di misura, del segmento che congiunge i due punti. Meno evidente è cosa debba intendersi per distanza di un punto da un segmento. Tolomeo propone di definire la distanza di un punto O da un segmento AB come la distanza di O dal punto medio M del segmento¹.

Questa definizione corrisponde bene all’immagine intuitiva che abbiamo quando il segmento è piccolo rispetto alla distanza del punto O. In questo caso infatti potremmo assimilarlo a un corpuscolo (il suo baricentro) come si fa in meccanica. Se invece la lunghezza di AB non fosse trascurabile e se il punto O fosse vicino ad un estremo del segmento, o addirittura sul segmento stesso, saremmo propensi a considerarlo molto vicino ad AB mentre la sua distanza dal baricentro M potrebbe essere anche molto grande.

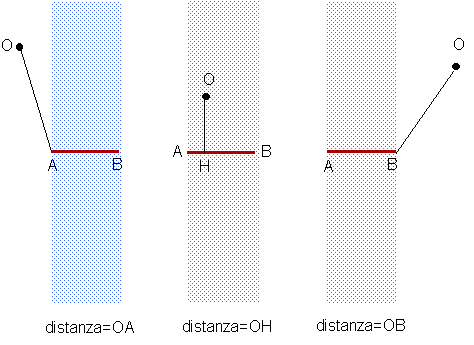
La definizione che proponiamo è più complicata di quella di Tolomeo ma tiene conto delle considerazioni precedenti:

Dato un segmento AB consideriamo la striscia di piano definita dalle rette ortogonali al segmento e passanti per i suoi estremi. Il punto O può trovarsi nel semipiano a sinistra o a destra della striscia o dentro la striscia stessa.
Definizione (di distanza di un punto da un segmento).
Se O è posto dentro la striscia di piano la sua distanza da AB è la misura del segmento di perpendicolare OH portata da O ad AB, altrimenti è la misura del segmento che unisce O all'estremo di AB a lui più vicino.

Esercizi

La definizione di distanza che abbiamo dato, diversamente da quella suggerita da Tolomeo, permette di affermare che un punto O ha distanza zero da AB se e solo se si trova sul segmento AB.

Vale inoltre il seguente teorema:

Teorema (sulla distanza di un punto da un segmento).
Dato un segmento AB e un punto O sia d la distanza di O dal segmento. In queste ipotesi ogni punto P del segmento AB ha distanza da O maggiore o uguale a d.

La dimostrazione va fatta nei tre casi considerati: se O è a sinistra l'angolo OAB è ottuso e quindi nel triangolo OAP il lato OP che è di fronte all'angolo ottuso è più grande del lato OA che è di fronte a un angolo acuto (Preliminari). Se O è nella striscia ortogonale allora OP è maggiore di OH perché in un triangolo rettangolo l'ipotenusa che è di fronte all'angolo retto è maggiore dei cateti che sono di fronte agli angoli acuti. Il terzo caso è uguale al primo.

Esercizi

Ulteriori esercizi possono rivolgersi al problema di derminare i punti equidistanti a due dati segmenti.

Stampa