|
In questo intervento cercherò di mostrare le motivazioni che mi hanno portato ad alcune scelte didattiche e all'utilizzo di alcuni strumenti.
Tenterò di evidenziare i limiti degli strumenti, il loro utilizzo, alcune modifiche apportate al percorso didattico.
Durante questa analisi mi concentrerò su due interventi uno di matematica ed uno di fisica
1
.
INTERVENTO DI MATEMATICA: matrici e vettori in una classe quarta di un liceo scientifico
Quando mi sono trovato ad effettuare questo intervento non avevo ancora seguito il corso della professoressa Catastini. La lezioni effettuate da
questa professoressa miravano, tra l'altro, a comprendere aspetti del processo cognitivo facendo particolare riferimento ai problemi legati
alla logica.
Questo capitolo nasce dalla revisione ed dall'approfondimento di un elaborato da me realizzato nell'ambito del corso tenuto dal suddetto docente
e mostra un'analisi a posteriori del lavoro di tirocini svolto nella classe IV D alla luce delle informazioni ricevute.
UTILIZZO DEL FOGLIO ELETTRONICO PER TRATTARE MATRICI E VETTORI.
Nel corso tenuto dalle professoresse Mentrasti e Proia abbiamo avuto modo utilizzare alcuni strumenti informatici che potevano essere applicati
alla didattica. Tra questi anche il foglio elettronico nella versione Microsoft Excel.
Ho scelto di utilizzare l'Excel invece di strumenti informatici appositamente studiati per la didattica per i seguenti motivi:
- L'Excel è uno strumento utile per la futura vita lavorativa dello studente è quindi utile che lo studente cominci a conoscere
tale strumento.
- Non è uno strumento rigido, il docente può scegliere come impostare il percorso didattico come meglio crede perché è egli
stesso a costruirlo
- Il ragazzo può sempre capire come un dato viene fuori (basta "cliccare" sulla casella e grazie a colori diversi vengono identificati i dati di origine e le operazioni compiute)
- Il programma ha una buona veste grafica: non bisogna sottovalutare l'importanza di tale aspetto sulla comprensione
- Nel programma sono implementate funzioni logiche che permettono di realizzare una sorta di "programmazione".
Contrariamente a quanto visto nella fase osservativa, il programma viene utilizzato non fine a se stesso ma per risolvere un problema inerente
argomenti del programma didattico.
Il foglio elettronico è stato utilizzato per sviluppare la capacità di ascolto e traduzione in un algoritmo di calcolo.
I ragazzi hanno lavorato in genere in gruppi di due persone. Ho avuto molta cura nel mettere insieme ragazzi che avessero diversa confidenza
con il programma, insistendo che la tastiera ed il mouse fossero utilizzati dal ragazzo con minore esperienza. Il ragazzo esperto doveva sforzarsi
di dare indicazioni cercando di ricorrere il più possibile ad un linguaggio verbale, invece di indicare una casella con il dito, doveva
designarla a parole (esempio: somma la terza componente del vettore V con la terza del vettore W).
Una prima parte delle lezioni è stata dedicata alla spiegazione dei comandi del programma applicati all'implementazione di alcune
operazioni (ad esempio prodotto di un vettore per uno scalare, somma di due vettori). Quando gli alunni hanno acquisito familiarità
con il programma le lezioni si svolgevano in modo diverso. Spesso io fornivo ai ragazzi soltanto una definizione, ad esempio prodotto scalare
di due vettori, essi dovevano capire il linguaggio formale utilizzato e tradurlo in uno schema di calcolo.
L'approccio utilizzato aveva lo scopo di sviluppare alcune di quelle che vengono definite capacità superiori:
- Capacità di comprendere un linguaggio specifico
- Capacità di comunicare con i compagni
- Capacità di elaborazione e comprensione
- Capacità di traduzione in un algoritmo implementabile nel foglio
La scelta di utilizzare il foglio elettronico mi sembrava particolarmente adatta all'argomento. Quando si fornisce una definizione riguardante
il calcolo matriciale, i ragazzi tendono a far perdere di significato ad alcuni fattori. Mi riferisco ad esempio agli indici dei componenti
dei vettori o degli elementi delle matrici. Penso che sia dovuto ad una questione visiva e di risparmio di memoria e concentrazione operata
inconsciamente dagli studenti.
Spiego meglio questa frase. Se i ragazzi sanno di non dover utilizzare immediatamente una definizione tendono ad affrontarla con sufficienza,
risparmiano energie e sottovalutano le cose che sembrano loro meno importanti: mi riferisco agli indici (che oltretutto sono scritti in basso
e in piccolo). Questo comporta che normalmente i ragazzi credono di avere compreso una formula o una definizione ma in realtà non
è così.
Nella situazione da me proposta i ragazzi erano costretti ad applicare immediatamente la definizione fornita. Dato che il lavoro era svolto da
coppie di ragazzi, gli studenti si rendevano immediatamente conto se un definizione o una formula non era stata compresa.
Rivedendo il lavoro svolto in base alle indicazioni della professoressa Catastini mi sono reso conto che i motivi che mi hanno condotto
alla scelta di questo strumento sono stati anche altri. Questi motivi investono il funzionamento del cervello.
Durante le lezioni con il foglio elettronico ho cominciato a notare comportamenti diversi degli studenti.
Se lo scopo degli studenti è ottenere la prima componente del vettore W somma di V e Z esistono due diversi modi con cui i ragazzi
hanno operato.
- Ci sono alcuni ragazzi che si ponevano in una casella e scrivevano "= C3+F3" dove la casella C3 conteneva V1 e la casella F3
conteneva Z1.
- Altri ragazzi tendevano al lavorare diversamente, scrivevano l'uguale "=" andavano col mouse sulla casella C3 "cliccavano" poi
scrivevano "+" e andavano a "cliccare" su F3. Questo tipo di studenti non si preoccupava della designazione della componente ma solo della
sua ubicazione spaziale all'interno del foglio. Vale a dire che questi ragazzi non sapevano affatto il nome di
V1( vale a dire la sua designazione C3 all'interno del foglio) ma preferivano individuarlo "spazialmente".
I ragazzi appartenenti al primo gruppo comunicavano con il compagno per via verbale i secondi con le mani (per indicare un elemento mettevano il
dito sopra lo schermo contrariamente alle indicazioni fornite).
Questi comportamenti degli studenti sono legati a stili cognitivi che possono differire tra loro. L'argomento che sto per affrontare è
molto delicato, facilmente criticabile poiché è ancora argomento di studio e dispute scientifiche, ma in base a quanto appreso nel
corso della professoressa Catastini provo ad interpretare i due diversi comportamenti nel modo seguente.
I ragazzi appartenenti al primo gruppo manifestano nel loro pensiero una forte componente analitico-verbale e prediligono un approccio
formale e rigoroso.
I ragazzi appartenenti al secondo gruppo mostrano un approccio di pensiero più legato alle figure e all'aspetto spaziale.
Rivedendo il lavoro fatto mi sembra chiaro che lo strumento Excel offre un mezzo per integrare le due intelligenze. Quando si "clicca" con
il mouse su una casella compare la formula implementata, Con colori diversi si mettono in evidenza i dati di partenza che sono quadrettati
con i colori corrispondenti a quelli della formula. L'integrazione dei due aspetti è palese.
Il fatto che i ragazzi lavorassero in gruppi di due, ha favorito lo scambio di informazioni, quando si verificava che due tipi di intelligenze
diverse lavoravano insieme si avevano i migliori risultati. C'era un iniziale contrasto dovuto al fatto che i problemi venivano affrontati
in modo diverso ma il procedere insieme alla fine arricchiva entrambi. Dove un ragazzo aveva problemi, interveniva l'altro. Il risultato ottenuto
in termini di comprensione e coinvolgimento degli studenti è stato buono, ho recuperato l'attenzione di molti studenti, la partecipazione
generale è stata elevata, gli studenti hanno lavorato e si sono impegnati, le ore di laboratorio informatico sono state divertenti per gli
studenti, anche il compito di verifica finale ha dato buoni risultati.
Penso che il tentativo di integrazione tra aspetto visivo e aspetto formale abbia giocato un ruolo importante per i risultati ottenuti.
Tutte le considerazioni precedenti sul tipo di intelligenza non sono state fatte al momento di decidere lo strumento da utilizzare per questo
percorso didattico ma solo a posteriori; i risultati ottenuti non sono, quindi, frutto di una riflessione cosciente effettuata in fase di
progettazione. Mi sono chiesto quali fossero stati i veri motivi che mi avessero spinto all'utilizzo di questo strumento.
Credo che la scelta sia stata dettata non dalle esigenze degli studenti ma dalle mie. In particolare credo che la scelta del foglio elettronico
derivi dal modo di lavorare del mio cervello, che non si basa su una rigida dominanza analitica: mi sono orientato ad uno strumento che integrasse
i due tipi di intelligenze: spaziale e linguistica: era lo strumento per me più comodo.
Devo inoltre considerare il fatto che soffro di una forma lieve di dislessia. Per me è facile invertire l'ordine delle lettere. Era
dunque molto probabile che in una lezione mi confondessi tra Mij e Mji, con effetti deleteri soprattutto su quei ragazzi
che si basavano
fortemente su indizi linguistici. Infatti se mi fossi sbagliato a scrivere la formula per ottenere il generico elemento della matrice
prodotto
i ragazzi che hanno un intelligenza spaziale non se ne sarebbero nemmeno accorti poiché avrebbero trascurato la definizione formale e
linguistica (la formula), avrebbero prestato attenzione alla parte spaziale della definizione, memorizzando semplicemente che l'elemento
alla riga j e alla colonna k della matrice prodotto era il prodotto scalare tra la riga j della prima matrice e la colonna k della
seconda. Nella loro rappresentazione mentale j e k della frase precedenti sarebbero scomparsi nel loro aspetto di lettere acquisendo un
aspetto geometrico. La riga j è una linea orizzontale o un rettangolo che contiene elementi di una riga o un riquadro evidenziato
che emerge da un'altra struttura geometrica. Quello che importa sono le posizioni reciproche; quello che conta è lo spazio.
In definitiva la scelta che mi ha condotto all'utilizzo del foglio informatico è stato quello di portare la spiegazione in un ambiente
che mi fosse più consono, gli effetti positivi sulla classe sono in parte da considerarsi degli effetti non progettati anche se
estremamente positivi.
Se la fase di lavoro con il computer ha avuto come conseguenza che gli studenti hanno integrato due aspetti della mente, quello verbale
e quello spaziale, il proseguire dell'intervento, le difficoltà incontrate in successivi interventi hanno fatto si che per me in quanto
docente nascesse la convinzione che in alcuni casi è necessario lavorare su piani distinti. In particolare dovevo affrontare problemi
come la spiegazione di tecniche di dimostrazione che ho scelto di affrontare nel campo linguistico che per il tipo di intelligenza da me
posseduto equivale a giocare fuori casa. Di seguito illustrerò come sono giunto ad affrontare le tecniche di dimostrazione, i problemi
incontrati nella spiegazione.
LIMITI NELL'UTILIZZO DEI SOFTWARE.
Durante l'utilizzo del foglio elettronico ho cercato di far capire uno degli insegnamenti principali che ho ricevuto dal corso tenuto dal
professor Ghione nel primo anno SSIS. Durante il corso il professore ci ha mostrato l'utilizzo del Cabri nella geometria mettendo in luce
come uno dei problemi principali fosse quello di confondere l'evidenza grafica con una dimostrazione oggettiva di un teorema.
Nel caso del foglio Excel bisogna stare attenti ad approcci di tipo sperimentale.
Il programma ha avuto, infatti, anche un utilizzo particolare ed improprio: è stato utilizzato per convincere gli studenti di alcune
proprietà di matrici e vettori senza dimostrarle. Ad esempio il fatto che una matrice con due righe uguali abbia determinante uguale
a zero è stato mostrato ai ragazzi senza darne una vera e propria dimostrazione. Essi hanno implementato il calcolo per ottenere il
determinante (non è stato utilizzato quello presente già tra le funzioni del programma), hanno immesso matrici con righe uguali
a loro piacimento fino a che non si sono convinti della veridicità della proprietà. Bisogna, però, dire che gli studenti
hanno usato questo approccio al problema consci del fatto che non è una dimostrazione e, quindi, le conclusioni potrebbero
essere errate. Questa coscienza è nata da un lavoro di convinzione che deriva da esempi reali. All'inizio del corso ho definito
i vettori linearmente indipendenti. Ho fatto implementare con l' Excel l'algoritmo per provare la combinazione lineare di tre vettori di
R3. Ho poi assegnato tre vettori particolar ed ho chiesto loro di trovare a verificare se questi erano o meno indipendenti. I
ragazzi hanno provato a cambiare i coefficienti della combinazione per ottenere un vettore nullo senza riuscirvi. In base all'approccio
utilizzato si poteva desumere che i tre vettori erano indipendenti. In realtà non lo erano ed ho fornito i valori dei coefficienti
per annullare la combinazione.
Abbiamo riflettuto a lungo sulla necessità di utilizzare tecniche di dimostrazione affidabili e in particolare sull'affidabilità
del controesempio come tecnica dimostrativa.
NECESSITÀ DI UNO STRUMENTO RIGOROSO - LA DIMOSTRAZIONE PER ASSURDO - PROBLEMI INCONTRATI E SOLUZIONI ADOTTATE
Se è vero che la necessità di utilizzare tecniche di dimostrazione rigorose è stato compreso dai ragazzi con chiarezza,
il modo con cui ho introdotto la tecnica di dimostrazione per assurdo è stato per i ragazzi dispendioso. Il motivo di queste mie
difficoltà mi sono state chiare solo dopo aver seguito il corso tenuto dalla professoressa Catastini.
Per chiarire la tecnica di dimostrazione per assurdo sono stati necessari tre interventi.
Una volta introdotta la necessità delle tecniche di dimostrazione ho chiesto agli alunni se conoscevano la tecnica di dimostrazione
per assurdo. Ho notato con piacere che gran parte degli alunni aveva qualche reminiscenza, una ragazza ricordava la definizione a
memoria (la tecnica di dimostrazione per assurdo dimostra che all'ipotesi segue la tesi dimostrando che alla negazione della tesi segue la non
veridicità della ipotesi, da cui l'assurdo). Visto la risposta positiva della classe, dopo aver ricordato cosa è la tesi e che cosa
è l'ipotesi, ho deciso di mostrare direttamente il funzionamento di questa tecnica applicata ad un teorema sui vettori, sicuro che
l'applicazione di questa tecnica sarebbe stata più esplicativa di qualsiasi trattazione teorica. Il teorema in questione è quello
che afferma che se due vettori sono linearmente indipendenti, allora nessuno di essi può essere un vettore nullo.
L'approccio scelto è risultato errato: i ragazzi capivano i singoli passaggi ma sfuggiva loro il senso generale e lo scopo del mio procedere.
Visto che l'ora di lezione volgeva al temine ho rimandato i chiarimenti al giorno successivo.
Pensavo che il principale motivo del mio fallimento fosse quello che i ragazzi, anche conoscendo la definizione, non ne avevano capito il senso
profondo. Per la lezione successiva ho deciso di affrontare l'argomento, portandolo su un piano generale ed astratto. Ho cominciato con lo
spiegare il significato della implicazione semplice indicata con il simbolo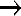 
cercando di mettere in evidenza che p 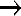q è falsa solo se p
vero e q falso. Ho cercato di far capire il senso di questo connettivo logico presentando un esempio tratto dalla vita comune.
Ho cercato di spiegare che l'implicazione: " se piove prendo l'ombrello" è falsa solo se non prendo l'ombrello e piove e continua a rimanere
vera se è falso che piove ed è vero che prendo l'ombrello. Il percorso è poi continuato con la realizzazione delle tavole di
verità al fine di dimostrare che il predicato i 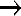t e il predicato
non(t) 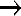non(i) hanno lo stesso valore di verità e falsità
indipendentemente dal valore di verità e falsità della tesi e della ipotesi. La mia intenzione era quella di implementare queste tavole
in una pagina Excel grazie all'utilizzo delle finzioni logiche.Prima della loro implementazione un ragazzo aiutato dalla classe ha realizzato
le tavole alla lavagna.
Durante il riepilogo a fine lezione comincio a fare qualche domanda ad alcuni alunni. Il dialogo si fa serrato ed ad un certo punto mi sento porgere
questa domanda:" Professore per quale motivo anche se non piove prendo l'ombrello?"
Mi accorgo di aver nuovamente fallito, il lavoro fatto aveva avuto come effetto che i ragazzi erano in grado di compilare una tavola di verità
ma non avevano afferrato il senso dell'implicazione semplice né il senso della dimostrazione per assurdo.
Capisco che l'esempio dell'ombrello e della pioggia è stato forviante. Non abbandono l'idea di affrontare l'argomento, conscio che le tecniche
di dimostrazione servono a sviluppare quelle capacità logiche che costituiscono un'abilità superiore nonché trasversale. Penso a
lungo a come impostare l'incontro successivo e cerco di elaborare una situazione di deduzione più semplice.
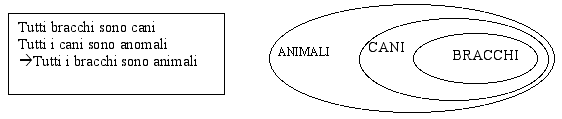
Ho posto agli alunni il seguente problema:
"voi possedete un'enciclopedia dei funghi. Tale enciclopedia è costituita da due volumi: i funghi velenosi ed i funghi non
velenosi.
Vostro cugino arriva a casa con un fungo rosso a puntini bianchi e vi chiede un parere su tale fungo sapendo che voi possedete la sopracitata
enciclopedia. Voi andate a cercare il volume che contiene tutti i funghi velenosi perché volete dimostrare il fungo raccolto è velenoso:
Fungo rosso con puntini bianchi velenoso
Fr-b V
Vi accorgete che il volume con i funghi velenoso è stato smarrito mentre ancora possedete il volume con i funghi non velenosi. Come fate
a dimostrare che il fungo raccolto è velenoso?"
I ragazzi hanno capito in breve tempo che dovevano consultare il libro dei funghi non velenosi e vedere che non ce ne era nessuno rosso con i puntini
bianchi
non(V) non(Fr-b)
i ragazzi hanno capito anche che l'implicazione non(Fr-b) 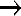non (V) è
falsa ed estremamente pericolosa. Significherebbe desumere
che i funghi che non sono rossi con i puntini bianchi sono non velenosi, questa deduzione porta ad una sicura intossicazione dovuta ai funghi velenosi
che non sono rossi con i puntini bianchi.
Il corso delle lezioni ha subito una svolta. Una volta afferrata la tecnica della dimostrazione per assurdo, la sua applicazione ai teoremi
relativi alle matrici è stato più agevole.
Il corso tenuto dalla professoressa Catastini mi ha fornito una chiave di interpretazione a posteriori di quanto avvenuto in classe ed indicazioni
su come modificare il lavoro.
Durante il primo tentativo ho sopravvalutato la capacità di memorizzazione degli alunni. Durante un processo logico è difficile che uno
studente riesca a tenere a mente più di 7 unità informative. Faccio riferimento ad una memoria di breve periodo che è funzionale
al ragionamento. Nel caso del primo tentativo (dimostrazione applicata direttamente ad un teorema di matematica) i ragazzi dovevano memorizzare molti
oggetti: la tecnica di deduzione, quale è l' ipotesi (ammesso che i si ricordano che cosa è l'ipotesi),quale è
la tesi ...
La tesi fa riferimento ad un concetto nuovo: vettori linearmente indipendenti devono, quindi, ricordarsi molti altri oggetti: che cosa è una
combinazione lineare, che cosa sono i coefficienti...
Per farla breve ho commesso un errore di valutazione grave. Molte delle cose che utilizzavo per la deduzione si trovavano per me all'interno della
memoria a lungo termine. Gli oggetti che si trovano nella memoria a breve sono dunque pochi ed il ragionamento procede senza intoppi.
Per gli studenti molti dei parametri che per me si trovavano nella memoria a lungo termine dovevano essere memorizzati nella memoria a breve termine,
ne consegue che la deduzione è difficile se non impossibile.
Quanto accaduto fa capire quanto la memoria influenzi le capacità logiche.
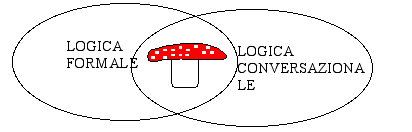
Nel secondo intervento ho commesso un errore di tipo diverso. La logica normalmente utilizzata dai ragazzi è una logica di tipo
conversazionale. Tale logica permette delle inferenze che la logica formale non ha. Il motivo principale che tale logica subisce una
contaminazione forte dal mondo reale di tutti i giorni e dal vivere concreto. È come se il senso pratico impedisse al nostro cervello di
considerare ipotesi irreali: che senso ha portarsi l'ombrello se non piove!!!
L'ultimo intervento ha funzionato per una serie di motivi.
- Innanzi tutto l'esempio è stato inserito in un contesto (in questo caso contesto familiare) che serve per "compattare" ed unire i
vari elementi in gioco.
- Gli oggetti del ragionamento (funghi) sono usuali, non occupano memoria a breve termine perché contenuti in quella a lungo termine.
- Nel caso in questione la logica di tipo conversazionale non entra in contrasto con quella formale. Il cervello non può permettersi
di trascurare nessuna delle ipotesi in gioco (si pensi al caso di funghi velenosi che non sono rossi con i puntini gialli).
Pensando a posteriori all'intervento effettuato penso di aver perso un'occasione: dovevo sfruttare gli errori commessi marcando chiramente
il confine tra logica formale e logica discorsiva mostrando il fatto che l'esempio dei funghi si trova nella loro intersezione.
RIFLESSIONI A POSTERIORI. PROBLEMI DI LINGUAGGIO E DI MEMORIA.
L'intervento didattico effettuato in questa classe e le difficoltà incontrate mi hanno fatto riflettere su i problemi di apprendimento degli
studenti. Alcuni di questi problemi sembrano essere riconducibili a due grosse tematiche: la memoria e il conflitto di interpretazione di testi
o frasi.
Alla memoria si riconosce anche una funzione di elaborazione dei dati immagazzinati ed una capacità selettiva nell'ambito delle conoscenze
da fissare, che si ricordano, che vengono evocate. Mi spiego, quando ci troviamo di fronte ad un dato osservato, il nostro cervello decide se
immagazzinare o meno il dato, col passare del tempo il ricordo viene rielaborato, modificato, ricollocato, in parte o del tutto cancellato. L'effetto
del tempo su un ricordo non è soltanto negativo, alcuni particolari scompaiono ma altri prendono nuovo senso. Se avviene una elaborazione, se
il ricordo è collegato ad altri eventi esso assume un significato di maggiore importanza che nel momento di acquisizione. Si pensi ai films
polizieschi: un particolare registrato all'inizio banale diventa in seguito quello che inchioda il colpevole di un delitto. Particolare
interesse per l'insegnamento riveste il momento di evocazione di un ricordo. Si pensi al celebre scrittore francese Marcel Proust, che nel
libro "alla ricerca del tempo perduto" ci descrive come il profumo il sapore, la vista di un dolcetto ("La Madelaine") scatena in lui una serie
incredibile di ricordi, sensazioni, emozioni della sua giovinezza. Proprio Proust ci può venire in aiuto per capire quali rimedi usare per
migliorare il rendimento della memoria e ottenere migliori prestazioni nella risoluzioni di situazioni problematiche. Due tecniche per migliorare
il ricordo sono quelle di creare un contesto e produrre associazioni di idee. Ad esempio l'euro vale 1936,27 L. Mi ricordo questo numero poiché
mio padre è nato nel 1936 (prima associazione) e mia sorella ha compiuto 27 anni quando è entrato in vigore l'euro
(seconda associazione). Per ricordarmi la cifra creo un contesto: mio padre che regala un euro a mia sorella per il suo compleanno.
La creazione di un contesto familiare sembra essere una chiave per entrare e per uscire con maggior facilità dalla memoria degli
studenti. Il contesto ha la funzione di legame tra vari aspetti di un ricordo, permette di immagazzinare e riprendere un ricordo con maggiore
facilità.
L'altra tecnica fondamentale per ricordare è quella visiva. Grande parte delle informazioni che giungono al cervello sono stimoli
visivi. L'euro per me è associato a una rappresentazione mentale che è soprattutto visiva: l'immagine di mio padre che dona la
nuova moneta a mia sorella. Si tratta di una specie di fotografia. Forse ho scelto questa tecnica per ricordare il valore dell'euro in
lire perché è quella più adatta al mio modo di pensare. É possibile che alcuni persone avranno meno difficoltà a
memorizzare direttamente le sei cifre del valore dell'euro piuttosto che cercare di trovare una qualche associazione possibile con contesti
familiari.
Durante l'insegnamento mi capita di suggerire associazioni di idee che aiutino i ragazzi nella memorizzazioni. Alcuni ragazzi ne traggono
giovamento da questi miei suggerimenti, altri li trovano inutili, superflui. Sembra, dunque, che la memoria abbia un carattere del tutto
personale e legato al tipo di intelligenza del ragazzo.
Un'errata conoscenza della memoria non è stato l'unico motivo di problema nel corso dell'intervento di tirocinio precedentemente
esposto. La difficoltà di soluzione di vari problemi, infatti, dipendono spesso dal conflitto di interpretazione, dovuto al fatto
che i testi che veicolano tali problemi, pur essendo formulati nella stessa lingua usata dagli studenti, fanno riferimento ad un codice
di interpretazione diverso. Anche in questo caso possono venirci in aiuto tecniche che "compattino" le unità di informazione e le loro
relazioni. Si pensi ad esempio ai sillogismi che possono essere illustrati capiti e risolti grazie a semplici figure.
CABRI. UN TENTATIVO DI INTEGRAZIONE TRA INTELLIGENZA SPAZIALE (FIGURE) ED INTELLIGENZA VERBALE (LINGUAGGIO)
Ho cercato di applicare le riflessioni precedenti che mi derivavano principalmente dal corso della professoressa Catastini ad un caso
reale. L'occasione è venuta dal corso del professor Ghione ha illustrato alcuni aspetti dell'evoluzione storica della matematica. Il
professore ha spronato gli studenti ad illustrare alcuni teoremi di geometria grazie all'utilizzo del programma Cabri.
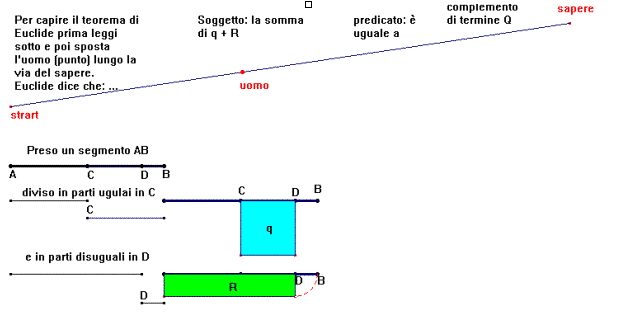
Il teorema che ho illustrato è la proposizione 5 del secondo libro degli "Elementi" di Euclide che recita:
Se si divide una retta in parti
uguali e disuguali, il rettangolo compreso dalle parti disuguali della retta, insieme con il quadrato della parte compresa fra i punti di
divisione, è uguale al quadrato della metà della retta.
Tale teorema per essere spiegato e compreso si scontra con problemi di memorizzazione e di linguaggio. Il Cabri si dimostra uno strumento agile
e flessibile adatto a superare tali problemi, esso permette di realizzare figure dinamiche che si muovono col procedere della
spiegazione. Quando gli studenti aprono la schermata si trovano di fronte la seguente figura.
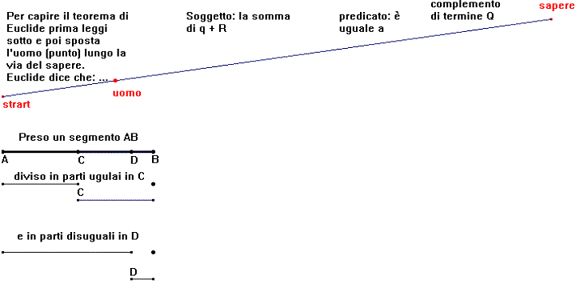
In questa prima fase ho cercato di creare un contesto : la via del sapere. La strada che è percorsa dal puntino rosso
"l'uomo" è una realtà un percorso che unisce varie parti di una frase , l'obiettivo è il sapere, vale a dire
la comprensione della frase.
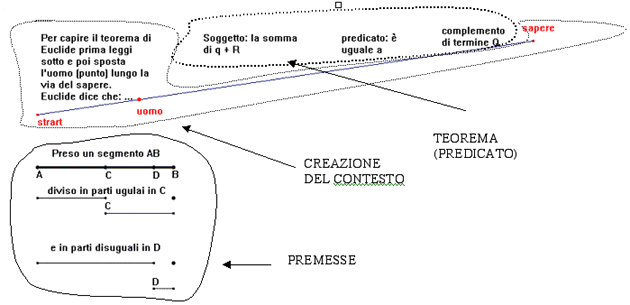
Le premesse sono separate dal teorema, sono chiarite graficamente. Il predicato non è chiaro nei particolari
(non si sa che cosa sono q R e Q) ma si capisce quale è il carattere generale del teorema (vale a dire che la somma di due oggetti è
uguale ad un altro oggetto). In questa fase è inutile definire il particolare poiché il ragazzo può perdere
il senso generale.
A questo punto quando sono chiare le linee generali lo studente comincia a muovere il puntino rosso ("l'uomo" nella via del sapere). La spiegazione
del predicato diventa una spiegazione grafica poiché con il muoversi del puntino compaiono i soggetti q e R.
A questo punto i ragazzi avranno afferrato quale è il soggetto da un punto di vista grafico (cognizione spaziale) e si può chiedere
loro di dare una definizione a parole di q e R (passaggio a una cognizione di tipo verbale). Contemporaneamente q e R sono presentati in una posizione
reciproca diversa.
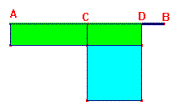
Inizia la riorganizzazione delle figure che caratterizza l'apprendimento di questo teorema di geometria. La ristrutturazione del campo cognitivo
avviene mediante la rottura di figure e la composizione di altre.
Mano mano che il puntino rosso viene spostato verso l'alto (l'uomo segue la via del sapere) le figure, grazie al software Cabrì, si animano e
si muovono facilitando al massimo questo processo.
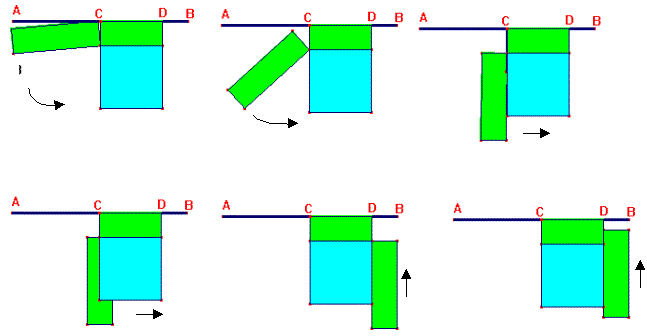
Quando l'uomo (puntino rosso) finisce il percorso del sapere al ragazzo è chiaro quale è il complemento di
termine Q il quadrato di lato CB. Il teorema è chiaro nelle sue linee essenziali e nei particolari. Il pensiero verbale è stato
portato avanti in parallelo alla sua traduzione in figure in movimento cercando in questo modo di integrare i due processi cognitivi.
La scelta di far rientrare l'animazione in una sola schermata è legata alla necessità di rendere il processo unitario. Alla fine del
percorso le premesse, soggetto, complemento di termine rimangono sempre visibili per ridurre i problemi di memoria al fine di far concentrare
lo studente sul senso generale e sulla ristrutturazione delle figure.
Una volta capito il teorema i ragazzi possono variare i parametri in gioco, vale a dire le lunghezze relative dei segmenti.
A questo punto è necessario sottolineare la necessità di una dimostrazione formale. Si sottolinea agli studenti che Lo strumento
informatico utilizzato serve a illustrare e non a dimostrare. A questo punto la dimostrazione può essere richiesta agli studenti che possono
scegliere di seguire una strada di dimostrazione parallela all'animazione o trovare una loro strada.
In questa fase il docente deve mettere in evidenza le cose che graficamente sembrano ovvie e che in realtà vanno dimostrate.
Se si facilita lo studente a superare difficoltà di comprensione e di memorizzazione si possono indirizzare le sue energie su aspetti
più creativi della matematica (come ad esempio trovare una propria strada per una dimostrazione).
|
|
