Il pensiero "naturale" e la didattica della matematica: alcune riflessioni

di Vasco Abiuso

Nel corso di Processi cognitivi e didattica della matematica, tenuto dalla prof.ssa L. Catastini, si è visto che il pensiero logico-formale non è una acquisizione spontanea della mente adulta. ¹ .
Analizzando alcune caratteristiche costitutive del cervello in relazione ai processi mentali che questo produce, si è visto come la formazione del pensiero (dal dato percettivo "elementare" alla formulazione di un ragionamento "astratto") è sempre un evento complesso a cui partecipano una molteplicità di fattori concomitanti. Accenno soltanto al fatto che, per esempio, il "riconoscimento" di un pentagono è un evento che richiede che si verifichino almeno le seguenti circostanze:

• occorre la corretta integrazione dei dati "interpretati" dai due emisferi (la forma della figura viene "interpretata" dall'emisfero destro, mentre il numero di spigoli è "contato" dall'emisfero sinistro);
• occorre che si conosca già la definizione di "pentagono";
• occorre che il contesto sia tale che la persona possa "riconoscere" il pentagono (ad esempio il poligono potrebbe essere "mimetizzato" all'interno del contesto tramite una trama di colori o la presenza di altri elementi figurativi "fuorvianti").

Ma anche qualora il pentagono venga riconosciuto che cosa susciterà nella persona? Questo, oltre allo scopo per cui viene osservata la figura, dipende dalla sua storia personale, dalle sue conoscenze pregresse, dal suo carattere, dal suo stato emotivo. Tutti questi aspetti rientrano appieno titolo nel processo percettivo e contribuiscono, in modo diverso, a "caricare di significato" l'immagine che abbiamo "sotto gli occhi". Anzi si può con assoluta certezza dire che se tutti questi fattori non vengono stimolati il nostro cervello non è in grado di mettere in relazione l'insieme di dati visivi per formare un immagine definita (il pentagono, appunto). Per lui, e quindi per noi, il pentagono non esiste!
Ho sviluppato questo esempio per dire che nel "pensiero naturale" i dati conoscitivi (il sapere) sono inevitabilmente contestualizzati e sono strettamente legati ad aspetti emotivi e psicologici che sono soggiacenti al processo stesso di elaborazione della conoscenza. Ciò ha delle implicazioni notevoli che un insegnante deve saper riconoscere e comprendere. Se il sapere è contestualizzato e legato a stimoli di natura psicologica. si pueò capire come può accadere che un alunno vada molto bene in latino e in greco ma non riesce ad ottenere la sufficienza in matematica. Magari si può anche riuscire a trovare la strategia didattica che lo fa "migliorare" nella matematica ... ² D'altra parte, evitando gli aspetti psicologici sui quali non sono in grado di entrare, il pensiero naturale è un intreccio tra pensiero verbale e non verbale ("pensare per immagini"). Un buon insegnante dovrebbe saper riconoscere queste due componenti del pensiero anche per capire da dove nascono gli errori più frequenti che vengono commessi dai propri alunni. L'esempio "del pentagono" ci fa capire qualcosa sul pensiero per immagini (sul quale tornerò più avanti). Anche il pensiero verbale nasconde una serie di insidie che vanno conosciute per neutralizzarle. Se infatti parliamo tutti la stessa lingua (in Italia!) non diamo, pereò, lo stesso significato alle medesime parole. Questo aspetto nella conversazione quotidiana (o nella letteratura) dà ricchezza al linguaggio, favorisce la formazione di stili linguistici e narrativi personali, ecc, ma nell'insegnamento della matematica ha effetti a volte negativi. Possono infatti sorgere difficoltà per il fatto che si usano termini del linguaggio comune con una diversa accezione e che la comunicazione verbale non ammette, nello specifico della disciplina, logiche "discorsive" ma solo quelle strettamente formali.
Nella vita quotidiana, invece, si è abituati a dare alle parole il loro significato ordinario e si utilizza una logica "conversazionale" ³ .
Il docente può immaginare, ingenuamente, che si può superare l'ostacolo del linguaggio semplicemente dando, di volta in volta, le definizioni dei termini che utilizza. Ma questa appunto è una posizione ingenua in quanto ignora che solo contestualizzando tali significati essi possono essere integrati all'interno delle mappe mentali degli studenti altrimenti si risolvono in un lungo elenco di informazioni che, essendo decontestualizzato, deve essere necessariamente imparato a memoria. Si rischia in questo modo, però, un sovraccarico della "memoria di lavoro" dello studente che può impedire la comprensione generale dell'argomento trattato a lezione.
Il contrasto tra la logica formale e la logica conversazionale è ancora più delicato. Devo ammettere che non ci avevo mai riflettuto sopra prima di questo corso. Anzi, per certi aspetti è stato per me illuminante perché mi ha permesso di capire, retrospettivamente, tutta una serie di obiezioni che mi sono state poste dagli studenti del liceo classico nel quale insegno da due anni.
Devo dire che alcune di queste obiezioni mi avevano fatto tornare a casa davvero scoraggiato. Per affrontare questo aspetto può essere utile riportare alcuni esempi:
"Nella logica formale, il significato del quantificatore Alcuni è almeno uno forse tutti. Nelle lingue naturali, invece, il termine alcuni ha il significato di alcuni ma non tutti (Girotto, Il ragionamento, Il Mulino, 1994, Pg 61.)
Un altro esempio riguarda l'utilizzo della parola "o". Nel linguaggio comune può essere utilizzata sia in senso esclusivo, tipo "o sei vivo o sei morto" ( o è vero l'uno o è vero l'altro), sia in senso non esclusivo, tipo "possono entrare soltanto i nati in novembre o di lunedì" (possono essere veri entrambi). Nella logica formale, invece, la parola "o" viene utilizzata soltanto in senso non esclusivo.
Si può, infine,

...considerare un'altra caratteristica essenziale che differenzia il discorso "logico" da quello comune. Mentre in logica non sono ammissibili presupposti inespressi, essi sono un elemento ineliminabile del discorso comune, condizione della sua economicità e della sua efficacia. (Mosconi, Discorso e pensiero,Il Mulino, 1990, Pg. 127)

Di conseguenza nella didattica della matematica non solo si utilizzano termini con accezioni diverse da quelle usuali ma si utilizzano anche diverse regole del linguaggio ⁴ .
Questi esempi ci devono indurre a riflettere sul rapporto che si instaura tra docente e alunno durante una spiegazione, per esempio, di geometria. L'insegnante utilizza la lavagna per costruire figure e tracciare simboli, nel frattempo utilizza il linguaggio verbale per "spiegare" la dimostrazione. Egli sa che figure, simboli e parole acquistano significato nel contesto della logica formale che caratterizza la matematica come scienza. Ma anche gli alunni sono consapevoli di tutto ciè? Questo è il problema. Se non ne sono consapevoli, infatti, essi "ascolteranno" la spiegazione, "vedranno" le figure, "leggeranno" i simboli, ma sicuramente utilizzeranno spontaneamente il sistema di decodifica della logica conversazionale. Ora se è vero che: il pensiero comune procede (o, più precisamente, deduce) non in contrasto con la logica classica. (Mosconi,op. cit. pg. 147) è tuttavia vero anche che:

a) quando esigenze logiche ed esigenze psicologiche coincidono, pensiero comune e logica tendono alla concordanza;
b) quando esigenze logiche ed esigenze psicologiche non coincidono, il pensiero comune tende a ricorrere ad una logica più ampia e permissiva della logica classica, più adatta all'appagamento delle esigenze psicologiche.

E' in quest'ultimo caso che nascono molti "errori" di comprensione degli studenti. D'altra parte anche qualora logica formale e logica conversazionale giungessero allo stesso risultato, il risultato "non formale" sarebbe raggiunto in un modo epistemologicamente scorretto. Ma questo aspetto è quasi trascurabile di fronte al fatto che si sarebbe venuto meno ad uno dei doveri della didattica della matematica: far acquisire agli studenti le capacità e le competenze per formulare e sostenere un ragionamento ipotetico-deduttivo. E' stato, infatti, già detto che questa non è un'acquisizione connaturata allo sviluppo biologico dell'individuo. Di conseguenza va appresa (possibilmente a scuola!).

Vorrei riprendere le questioni fin qui affrontate mostrando una lezione di trigonometria da me svolta durante il tirocinio attivo in un Istituto Tecnico serale. In tale intervento ho fatto ampio utilizzo del laboratorio informatico dove ho utilizzato dei file di Cabri da me appositamente preparati. E' un intervento che ho svolto al primo anno SSIS dopo aver appreso le funzioni fondamentali di Cabri al corso del prof. Ghione e mentre stavo seguendo il corso del prof. Accascina.
Devo innanzitutto dire che la classe era composta da adulti lavoratori che per motivazioni diverse (non mi ci dilungo, anche se sarebbe interessante da analizzare nell'ambito del rapporto didattica-processi cognitivi) avevano deciso di riprendere lo studio dopo anni di abbandono. La situazione in cui mi sono trovato era veramente particolare, in quanto mi trovavo a dover interagire con persone con problematiche didattiche diversissime tra loro. Si tenga presente, inoltre, che erano tutti adulti e quindi con capacità cognitive e strutture di ragionamento ben radicate ⁵ .
Il tema del mio intervento didattico era l'introduzione della Trigonometria. Avendo fatto diverse ore di tirocinio osservativo in quella classe mi ero reso conto che mancavano molti concetti geometrici "elementari". Dovendo, nella prima parte della trattazione, ricorrere a molti concetti di geometria del piano, ho deciso di seguire una strada molto particolare (e mai tentata prima).
Poiché gli studenti avevano da poco seguito una serie di lezioni sui vettori e sulla moltiplicazione tra numeri complessi in base al modello vettoriale, decisi di introdurre le funzioni trigonometriche analizzando la rotazione del vettore unitario con origine nell'intersezione degli assi cartesiani. Dopodichè utilizzando le proprietà di simmetria assiale e centrale avrei ricavato le relazioni per seno e coseno tra angoli complementari e angoli associati.
Il metodo da me seguito è consistito nel dividere la lezione in due fasi: nella prima ho impostato lezione dialogata (con utilizzo tradizionale della lavagna) e nella seconda ho radunato tutti gli alunni (meno di dieci persone) intorno al Pc per "vedere" e "manipolare" i file di Cabri al fine di "riconoscere" quanto appena trattato.
Ho iniziato, quindi, la lezione disegnando alla lavagna la circonferenza goniometrica e analizzando le posizioni particolari del vettore unitario.

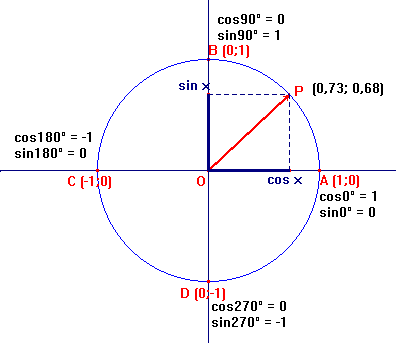
figura 1

In questo modo ho potuto affiancare alla rappresentazione cartesiana del vettore (già nota agli studenti) la sua rappresentazione trigonometrica. Introdotte in questo modo le funzioni di seno e coseno dell'angolo (misurato ancora in gradi), sono andato a studiare come varia il loro segno algebrico durante la rotazione (antioraria) del vettore. E' venuto così naturale caratterizzare in questo modo i quattro quadranti della circonferenza goniometrica:

Con questa analisi preliminare ho potuto mostrare che il seno e il coseno sono funzioni continue della variabile angolare x, assumono valori limitati tra -1 e 1, e sono periodiche di periodo 360^o (uso i gradi perché nella prima lezione non ho ancora introdotto i radianti).
Dopo di che ho illustrato le relazioni che sussistono tra le coordinate goniometriche del vettore unitario in diverse posizioni particolari: ho così introdotto gli angoli complementari e gli angoli associati.
Va detto che, nello stabilire le suddette relazioni tra le coordinate, ho sfruttato agevolmente le proprietà di simmetria che la classe aveva già studiato durante l'anno.
In particolare, le relazioni tra seno e coseno per angoli complementari le ho dedotte utilizzando le proprietà di simmetria rispetto alla bisettrice ⁶ .

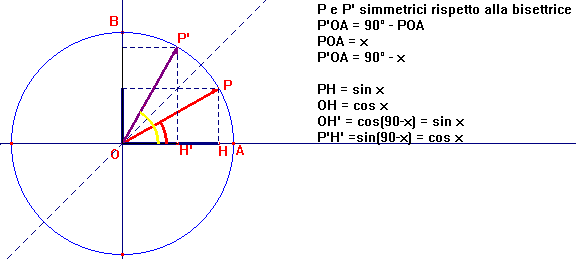
figura 2

Per stabilire il seno e il coseno di archi associati ho sfruttato, invece, la simmetria assiale e la simmetria rispetto all'origine.

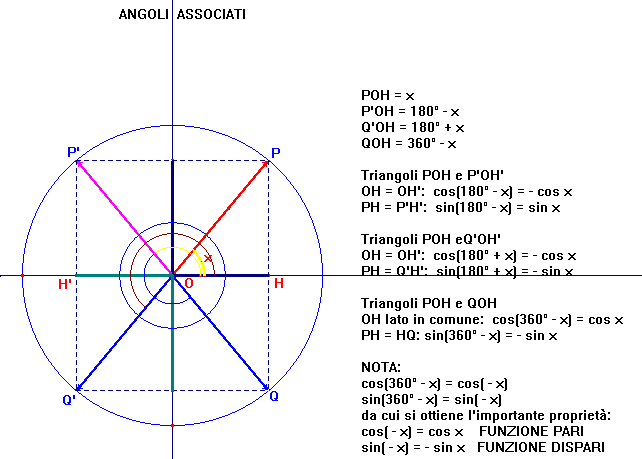
figura 3

L'analisi della figura mi ha anche consentito di mostrare che il seno e il coseno si comportano diversamente per inversione del segno dell'argomento, introducendo così i concetti di funzione dispari e di funzione pari.
Al termine della lezione ho invitato gli studenti ad avvicinarsi al Pc e ho mostrato tre file di Cabri che avevo preparato precedentemente in cui erano illustrati i concetti fondamentali affrontati a lezione. Ho poi effettuato delle stampe che ho consegnato agli alunni. Alla lezione successiva ho potuto notare con piacere che tutti avevano con sé le stampe e che alcuni vi avevano scritto delle proprie note personali.
Analizzando la successione delle fasi didattiche in cui la lezione è articolata, anche in relazione agli strumenti utilizzati e al contesto della classe, si possono riscontrare tutte le problematiche precedentemente espresse.
Lo studente, infatti, si trova "coinvolto" in un discorso verbale (la mia spiegazione orale) che può essere compreso soltanto se si mantiene una stretta sintonia con le immagini che di volta in volta vengono "rappresentate" alla lavagna. Ma la decodifica del linguaggio verbale e delle immagini seguono regole diverse, anche se alla fine dovranno integrarsi per costituire un'unica struttura dotata di significato.
Per esempio, per interpretare la Figura 1 si richiede di superare la seguente difficoltà: occorre fissare l'attenzione su come, al variare del punto P, variano le sue proiezioni ortogonali sugli coordinati. Si noti che non è banale. Se si deve considerare un vettore (o un punto) che "ruota" sulla circonferenza, l'elemento percettivo visivo che viene naturale considerare come principale è, appunto, il vettore (il punto). Ed invece tale elemento deve diventare secondario rispetto ad un'altra coppia di elementi che è, addirittura, difficile da visualizzare: le proiezioni ortogonali. L'utilizzo del Cabri, rispetto ai disegni a mano libera sulla lavagna, può essere risolutivo. Evidenziando le proiezioni del vettore (come in figura) e spostando il punto P, viene naturale osservare subito come variano proprio quelle proiezioni. La decodifica delle Figure 2 e 3 è chiaramente più complessa ma segue esattamente gli stessi principi. Si tratta sempre di indicare esplicitamente alla classe quali elementi della figura devono essere messi in relazione tra loro, quali sono i principali, quali sono i secondari e quali sono soltanto accessori. In questo modo si stanno fornendo le "regole" per decodificare correttamente le immagini, e poiché queste racchiudono (molto spesso) i concetti che cerchiamo di veicolare con il linguaggio verbale si può realizzare quella giusta sintonia che rende la comunicazione didattica efficace.
Si noti che nell'intervento di tirocinio attivo, come già detto, ho mostrato i file al termine della lezione permettendo agli alunni di manipolarli loro stessi. In realtà inizialmente avevo pensato di realizzare una lezione multimediale direttamente on line sfruttando la rete locale dell'istituto. Tuttavia problemi tecnici sopravvenuti nello stabilire la connessione tra i Pc del laboratorio mi hanno costretto a desistere.