|
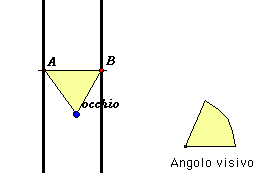
L'immagine animata che abbiamo realizzato permette di spostare l'occhio e anche il segmento AB che può essere allontanato dall'occhio col mouse.
Qua l’idea di parallelismo è
legata, come nel rinascimento, all’idea di equidistanza: la retta parallela a una retta r è descritta da un punto P che si muove
mantenendosi equidistante da r. Dunque in quest'ambito parallelismo ed equidistanza si equivalgono: una linea equidistante da una retta,
è una retta ed è parallela alla retta data, e viceversa. La stessa cosa non accade
nella geometria della sfera dove il luogo dei punti equidistanti da un cerchio massimo non è un cerchio massimo.
Nella geometria della visione dovremmo, per precisare i nostri presupposti, dare la definizione di "vedere allineato" e "vedere equidistante"
Definizione 1
Diciamo che tre punti A,B,C sono visti da O allineati se i tre raggi visivi OA, OB, OC stanno su uno stesso piano.
Da questa definizione segue immediatamente che se tre punti A, B, C stanno su una retta r, allora vengono visti come allineati poiché il piano
che passa r e per O contiene tutti i raggi visivi ottenuti con punti di r. L'essere "in fila" è dunque una proprietà che
non dipende dal punto di vista, è la prima proprietà invariante della geometria della visione: comunque guardi tre punti
allineati li vedo sempre allineati, una retta la vedo come una retta.
Definizione 2
Diciamo che due linee sono viste equidistanti tra loro se ai punti A dell'una corrispondono punti B dell'altra in modo che B si veda
equidistante da A qualunque posizione abbia A sulla prima linea.
Accadono ora vari fatti singolari trattati negli esercizi1. Ad esempio il vedere equidistante non si accompagna col vedere allineato.
La dimostrazione che indica Euclide per il teorema 6 è molto importante perché il procedimento seguito permette di ritrovare le prime tracce
di quello che poi sarà chiamato il punto di fuga. Euclide infatti dimostra che le due rette parallele non vengono mai viste equidistanti ma anzi
si vedono come se tendessero ad unirsi in un punto, poiché l'angolo visivo sotto il quale vedo due punti equidistanti sulle due rette, tende, come
la dimostrazione accerta, a zero.
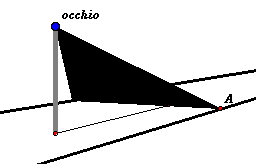
Euclide considera separatamente il caso in cui il punto di vista O sta sul piano delle due rette e il caso in cui O sta su piano diverso.
Nel primo caso la dimostrazione, una volta chiarito il contesto, è essenzialmente identica a quella del teorema 5.
Infatti, se l'occhio è interno
alla striscia compresa tra le due parallele, l'angolo visivo, man mano che i punti equidistanti AB si allontanano dall'occhio, diventa sempre più
piccolo, più piccolo di un angolo arbitrariamente dato (nel linguaggio moderno diremmo che il limite è zero). La circostanza che l'occhio si
trovi all'interno della striscia, non è, come per
il teorema 5, essenziale alla nostra dimostrazione. Il teorema vale in ogni caso purché si aggiunga un'ipotesi, che molto opportunamente Euclide
formula esplicitamente dicendo "visti da lontano", l'ipotesi cioè che il segmento AB sia abbastanza lontano dall'occhio. Qualunque sia la posizione
dell'occhio, dentro o fuori la striscia compresa tra le due parallele, da un certo punto in poi, l'angolo con cui vedo il segmento AB diventa sempre più
piccolo.
| |
|
|
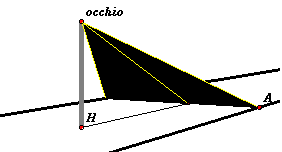
Nel caso in cui l'occhio si trovi fuori dal piano che contiene le rette parallele si proietta ortogonalmente l'occhio su quel piano e, quando questa
proiezione H è interna alla striscia, si procede essenzialmente al solito modo. Si divide l'angolo visivo, seguendo la dimostrazione suggerita da Euclide,
in due parti e si considerano i triangoli rettangoli OAK e OBK che si vengono a formare. Il triangolo OAK ha un cateto AK fisso e l'altro cateto OK
sempre più lungo, quindi l'angolo KOA tende a zero, e analogamente HOB.
Notiamo che nel caso speciale in cui la proiezione ortogonale H cade su una delle due rette, ad esempio quella per B, la dimostrazione diventa
più
semplice poiché dobbiamo considerare un solo triangolo rettangolo e l'angolo visivo AOK tende a zero dato che il cateto AK = AB è fisso (le
due rette sono equidistanti) e l'altro cateto OK diventa sempre più lungo.
Supponiamo ora che il punto H stia fuori dalla striscia compresa tra le due parallele, e supponiamo che sia, per fissare le idee, dalla parte di B.
La figura animata precedente ci permette di visualizzare questa situazione spostando col mouse il punto H nella posizione che vogliamo.
Consideriamo adesso la retta per H parallela alle due rette date, l'angolo AOK, per quello che abbiamo visto prima, tende a zero, e, a maggior ragione,
tende a zero l'angolo visivo AOB che è più piccolo di quello.
Possiamo quindi concludere affermando, con Euclide, che segmenti paralleli vengono visti come se
si avvicinassero sempre più tra loro, come se tendessero a un punto comune, ovunque sia il punto di vista, purché abbastanza lontano
dai segmenti stessi.
Questo risultato si estende ovviamente anche al caso in cui i segmenti paralleli tra loro siano più di due. Se abbiamo ad esempio tre rette parallele
e i punti A, B e C sulle tre rette in modo che muovendosi A sulla prima retta, B e C si mantengano equidistanti da A muovendosi sulle altre due,
allora, seguendo il teorema 6, possiamo concludere che B e C vengono visti avvicinarsi sempre di più ad A e, in definitiva, le tre rette
vengono viste come convergenti in un solo punto.
Il teorema 6 di Euclide può allora essere rienunciato affermando che:
Rette parallele vengono viste come rette concorrenti in uno stesso punto.
In particolare dei segmenti paralleli vengono visti come segmenti diretti tutti verso un unico "but", come dirà Desargues.
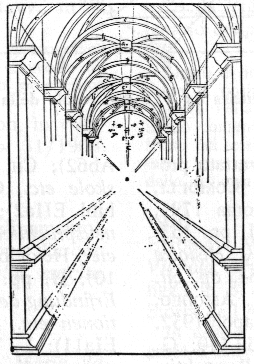
La "stanza delle maschere", scoperta nel 1961 a Roma sul colle Palatino che pare risalga al 30 a.C., è affrescata con uno straordinario dipinto che,
grazie a una prospettiva perfetta, fa sembrare l'ambiente, peraltro piuttosto angusto, molto più grande di quanto non sia in realtà.

Come si può osservare cliccando sull'immagine del dipinto, le colonnine poggiano su segmenti che, se prolungati, si dirigono a uno
stesso punto dove convergono anche gli tutti gli altri segmenti che, nella realtà che si vuol figurare, sono paralleli tra loro. Questo semplicissimo
accorgimento fa si che le linee disegnate si vedono, coerentemente col teorema di Euclide, come si vedrebbero se esistessero realmente: il pensiero visivo
ricostruisce esattamente l'ambiente rappresentato dando l'illusione della profondità.
Il fatto dunque che segmenti paralleli appaiono diretti verso uno stesso punto ci pare fosse ben noto, oltre che teoricamente, anche nella pratica pittorica,
fin dal terzo secolo avanti Cristo. Lo stesso Lucrezio riporta in versi questa conclusione:
3
|
|
|
Un portico benché abbia profilo costante,
e appoggi completamente su uguali colonne,
se si vede da una parte finale in tutta la sua lunghezza,
poco a poco si stringe nella punta di un cono sottile
congiungendo tetto e suolo, tutto ciò che sta a destra e a sinistra,
fino a terminare nella punta oscura di un cono.
Questa immagine ci sembra rappresenti bene i versi del poeta.
Il fatto che segmenti paralleli vengono visti diretti verso uno stesso punto suggerisce l’idea semplicissima di rappresentarli su un dipinto come segmenti
(punti allineati vengono visti allineati) che, se prolungati, convergono a un punto (il punto di fuga) come abbiamo visto per la stanza delle maschere.
Rappresentazioni
di segmenti paralleli che contraddicono questa regola dipendono dunque o da una mancanza di conoscenza teorica da parte dell'artista che non riesce a realizzare
ciò che vorrebbe, o da una scelta cosciente che consiste nel non voler rappresentare nel quadro il mondo come si vede secondo l'impianto euclideo.
Tutto ciò è stato per secoli dimenticato, distrutto da guerre violente e ricostruito per altre vie molto più tardi.
Nell'ultima cena di Duccio da Buoninsegna, ad esempio, gli spigoli laterali del tavolo sembrano all’occhio dell’osservatore contrari a come
dovrebbero apparire e le linee del soffitto che si suppone sia squadrato con segmenti paralleli non viene rappresentato coerentemente col teorema 6 di Euclide.
Ulteriori esempi di questo tipo si possono trovare nella scheda "La prospettiva lineare e il Quattrocento italiano"

Cliccando sul quadro appaiono i prolungamenti dei segmenti "paralleli".
Ben diverso è l'approccio di Leonardo da Vinci sia sul piano teorico che artistico. Scrive Leonardo:
Quelli che si innamorano della pratica senza scientia sono come nocchieri che entrano in naviglio senza timone o bussola, che mai hanno certezza dove si
vadano. Sempre la pratica deve essere edificata sopra la buona teoria, della quale la prospettiva è guida e porta e senza questa nulla si fa bene.
Il risultato di questa scelta è ben chiara nel suo Cenacolo dove la profondità della scena, perfettamente realizzata sul piano prospettico,
crea l'illusione in chi osserva l'affresco, di essere dentro quella scenografia, di vivere quel momento.

|
|