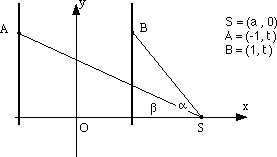
Una dimostrazione analitica e una sintetica
Fissiamo un sistema di coordinate come nella figura

Supponiamo che l'occhio si trovi in S e sia q l'angolo visivo ASB
q = a - b
con cui viene visto il segmento AB. Poiché
![]()
abbiamo:
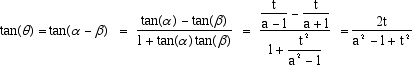
Da questa formula vediamo che la tangente dell'angolo visivo è zero per t = 0 e per t che tende all'infinito e quindi l'angolo q (t) si annulla per t = 0 e diventa sempre più piccolo man mano che il punto A si allontana da S sulla verticale. Per ragioni di continuità esisterà quindi una particolare posizione del segmento AB per la quale l'angolo ha un massimo. Per calcolare questa posizione basta trovare il valore di t che annulla la derivata della funzione q (t). Poiché
![]()
questo volore è quello che annulla la seguente derivata:
![]()
cioè
![]() .
.
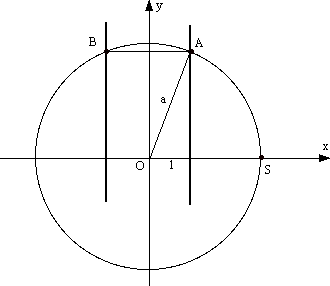
Notiamo che il risultato può essere facilmente interpretato geometricamente, infatti il valore di t trovato è la lunghezza di un cateto di un triangolo rettangolo con l'ipotenusa lunga come OS e l'altro cateto lungo 1. La figura mostra da che punto in poi l'angolo visivo ASB comincia a rimpicciolire tendendo a zero.
 .
.
Allo stesso risultato potevamo arrivare per via sintetica, senza servirci delle coordinate e delle derivate.
Data una qualunque posizione del segmento orizzontale AB, possiamo considerare la circonferenza che passa per A, B ed S. Il centro di questa
circonferenza deve trovarsi sull'asse del segmento AB che è fisso, indipendente dalla posizione di AB, inoltre l'angolo visivo
q = ASB è
tanto più grande quanto più piccolo è il raggio di tale circonferenza: il massimo angolo corrisponderà al minimo raggio e il
minimo angolo al massimo raggio.
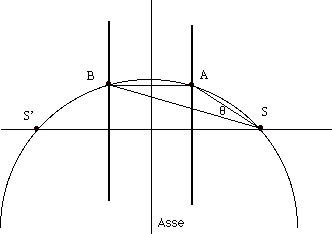
Poiché l'asse indicato in figura passa per il centro della circonferenza, il punto S' simmetrico di S rispetto a quest'asse appartiene alle circonferenze che stiamo considerando, ma questo punto è fisso, non dipende dalla posizione di AB. Dunque le nostre circonferenze passano tutte per S e per S' e hanno il centro sull'asse. Tra queste la più piccola è, come è facile convincersi, quella che ha il segmento SS' come diametro, e quindi l'angolo visivo sarà massimo per quella posizione come avevamo trovato per altra via. L' animazione che abbiamo realizzato illustra dinamicamente questa circostanza.