|
Lo svolgimento dell'esercitazione: il prospettografo
Lo strumento può venire presentato agli allievi illustrandone i diversi
precursori e insistendo sull'utilizzo che ne veniva fatto,
e sulla disinvoltura raggiunta grazie alle istruzioni impartite dai maestri agli
allievi.
Tutto questo trova una sua naturale integrazione in una breve trattazione della "profondità
degli ambienti" nella pittura da parte della disciplina di Storia dell'Arte,
evidenziando, attraverso le immagini, la notevole differenza tra rappresentazioni
prima e dopo la diffusione della prospettiva.
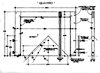
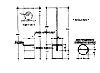
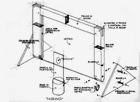
Il quadro di rappresentazione può, in una prima lezione venire presentato smontato per
poterlo assemblare con la collaborazione degli allievi, creando in questo modo, una sorta di laboratorio rinascimentale
dove la manualità si accompagna allo studio teorico. Per un buon
utilizzo servono dei piani di appoggio, tre o quattro banchi accostati dovrebbero
bastare, intorno si possono sedere gli allievi; su un lato del grande banco si
posiziona il prospettografo ed il mirino badando di rispettare, tra questi una
distanza di 50/60 cm. (misura utile alla estensione del braccio). Dietro al
prospettografosi faranno posizionare dagli allievi i modelli, quelli piccoli a
ridosso del quadro, mentre quelli più grandi andranno più distanti.
La fase successiva può muoversi in due direzioni:
1) quella più rapida: il docente si mette al mirino, dichiara l'oggetto che
vuole rappresentare ed inizia a lavorare, illustrandone le sequenze sino al
completamento; queste operazioni sono perfettamente visibili e conprensibili da
tutti gli allievi che vedono gradualmente ricostruirsi l'oggetto direttamente sul
vetro. Subito dopo si chiede loro di provare. E' importante che ogni allievo si misuri con l'esperienza, durante
queste operazioni il docente può perfezionare l'attività mostrando i raggi
visuali/proiettanti che uniscono il punto di vista del mirino e l'oggetto e la
conseguente proiezione sul quadro trasparente che li seziona.
2) quella meno rapida (ma assai efficace): dopo avere allestito gli strumenti
si toglie il quadro e con l'aiuto di listelli molto sottili si mostrano i percorsi
dei raggi visuali che, facendo vertice fisso dal mirino, "toccano" i vari vertici dei
solidi; quando viene riposizionato il quadro diviene assai più evidente il concetto di
"sezione" delle piramidi e coni visivi(alberti). Ora si può chiedere agli allievi di segnare,
sul vetro, quelle sezioni; il docente illustra le operazioni ma non mostra la procedura
in prima persona, insiste sulla rappresentazione di quell'oggetto sul quadro
trasparente grazie al traguardare nel mirino, ed invita gli allievi a cimentarsi,
a provare; poichè non serve alcuna attitudine alla materia, si può davvero invitare
chiunque a svolgere l'esercizio, perchè non può commettere errori, anzi, per qualche
allievo può divenire una piccola vittoria con un'immediata ricaduta nell'autostima.
Consapevoli della apparente difficoltà a ruota seguono tutti gli altri allievi.
In ambedue le direzioni si consiglia di allestire il "parco modelli" con
elementi geometrici, con spigoli, vertici e facce, poiché il disegnare verticalmente
sul vetro non è così agevole e comodo; infatti all'inizio è consigliabile far
definire, sul quadro trasparente, i soli vertici della figura, per poi proseguire,
con un righello, all'unione dei punti per descrivere gli spigoli, quindi colorare
le facce. La procedura viene in questo modo molto semplificata perché anziché traguardare tutti
i punti di uno spigolo basta traguardare gli estremi e congiunngerli, sul vetro, con una linea retta.
Questa scorciatoia si giustifica pensando che la proiezione conserva l'allineamento cioè che punti
allineati sullo spigolo dell'oggetto si trasformano in punti allineati sul vetro. Queste osservazioni
potranno formare una base sperimentale molto utile per creare quall'umus intuitivo necessario alla
introduzione delle trasformazioni proiettive da un punto di vista matematico.
Poiché l'esperimento crea normalmente molto interesse e curiosità nella classe
le rappresentazioni possono
proseguire con altri modelli meno semplici: l'architettura dell'aula (banchi,
pareti, soffitto, arredi etc.) sino ad arrivare all'ambito più difficile della rappresentazione quello della
figura umana, sempre che si trovi la disponibilità paziente di un allievo a fare da modello.
La restituzione grafica: ovvero la visione prospettica per mezzo dei raggi visuali
Dopo avere svolto l'esercitazione con il prospettografo (alla quale hanno
partecipato tutti gli allievi), si presenta l'ipotesi di restituire graficamente
su foglio lo stesso impianto ancora montato e ben visibile sul tavolo. La prima
elaborazione che si chiede di produrre sono le semplici Proiezioni Ortogonali di
uno dei modelli usati nella realtà
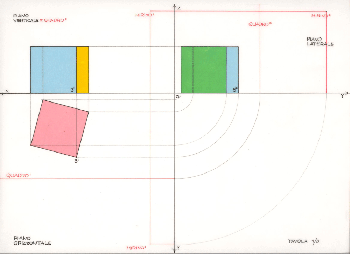
come si può notare l'elaborato sin qui
reso non è centrato rispetto al foglio, questo perchè oltre alle proiezioni della
figura si rende necessario inserire, sul Piano Orizzontale, il "quadro di
rappresentazione" (Q) ed il "mirino" (P.V., Punto di Vista). Questi a loro
volta andranno proiettati sui restanti piani (Verticale e Laterale). L'impianto
generale delle Proiezioni Ortogonali è ora completo, si può procedere con la vera
e propria prospettiva della figura, cioè con la restituzione dell'esercitazione
svolta con il prospettografo. Tornando a parlare di raggi visuali/proiettanti si
fa notare agli allievi il numero dei vertici della figura; si insiste nel ricordare
che anche col prospettografo sono stati attivati tanti raggi quanti i vertici della
figura. Così riproponendo le stesse condizioni è possibile unire, graficamente, il
punto di vista con le proiezioni dei vertici; elaborazione questa che viene ripetuta
per tre volte poichè tre sono i piani di proiezione. Le immagini così raggiunte
devono essere commentate ed in particolar modo quelle sul Piano Orizzontale e sul
Piano Laterale; infatti su questi due piani è ben visibile lo scorcio totale del
quadro di rappresentazione. L'intersezione tra questo ed i raggi proiettanti/visuali
determinano le tracce dei vertici della figura; le proiezioni di queste sul Piano
Verticale determinano la prospettività finale della figura.
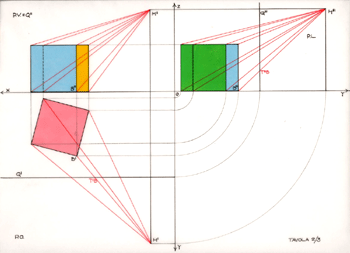
La successiva rappresentazione grafica è l'assonometria; indifferente è il
tipo, ma necessaria è la restituzione globale delle Proiezioni Ortogonali, compreso
il triedro. Scorrendo il lavoro si rivisualizza l'intero percorso della precedente
rappresentazione, in più si riproduce: l'effettiva figura, l'effettivo quadro di
rappresentazione, l'effettivo Punto di Vista e l'effettiva prospettività in pratica
l'intera esercitazione col prospettografo e le relative poiezioni ortogonali in una
sola immagine.
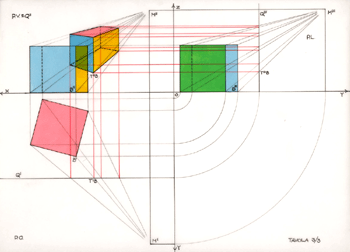
La seguente figura animate permette di muovere il punto di vista sul piano orizzontale
e su quello verticale, ruotare e traslare il cubo sul piano orizzontale, e spostare il prospettografo.
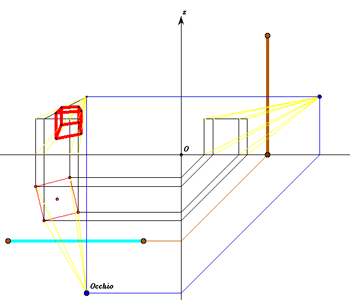
Il passaggio dalla prospettiva col metodo dei raggi visuali
alla prospettiva col metodo dei punti di fuga
Quando il metodo dei raggi visuali è stato ben consapevolizzato, il
prospettografo può avere un suo ulteriore utilizzo per avvicinare gli allievi ad
un altro metodo, quello dei punti di fuga (e per estensione dei punti di distanza
e dei punti misuratori).
Per venire incontro all'illustrazione di questo nuovo metodo occorre
abbandonare, momentaneamente, i modelli tridimensionali e proporre la prospettività
di una pavimentazione (una maglia ortogonale come esempio iniziale), poggiata,
quindi, sul piano orizzontale ed "accidentale" rispetto al vetro; per il prospettografo
tradurre questa griglia sul quadro di rappresentazione è gioco semplice.
Dalla sua osservazione è facile commentare che i giunti paralleli del pavimento man
mano che si allontanano tendono ad avvicinarsi, ed anche se questo non è possibile
confermarlo con una visione diretta, è possibile affermare che vadano a condurre in
un unico punto (facilmente realizzabile e condivisibile se si chiede agli allievi di
prolungare, con una riga, tutti i giunti tracciati sul quadro di rappresentazione).
Questa esperienza traduce in una attività di laboratorio l'impianto albertiano
basato sul concetto di raggio centrico e di punto centrico, e può essere utilmente accompgnata da una lettura diretta del
testo di Alberti.
In un pavimento ortogonale, posto obliquamente rispetto al quadro, verranno
confermati due punti che raccolgono i giunti ortogonali del pavimento (punti che d'ora
in poi chiameremo Punti di Fuga). Se tra questi due punti si fa passare una retta
si può notare un perfetto parallelismo col piano orizzontale ed infatti quella retta è,
per la prospettiva, l'Orizzonte geometrico posto, da far notare, alla stessa
altezza del Punto di Vista. Successivamente si può chiedere agli allievi di proiettare
sul banco di lavoro, e perpendicolarmente rispetto all'Orizzonte, i due punti di fuga; la retta che li unisce,
all'intersezione tra il quadro di rappresentazione ed il
banco di lavoro, d'ora in poi si chiamerà Linea di Terra (termine non nuovo,
poichè già corrispondente alla Linea di Terra dell'altra prospettiva).
Sin qui
l'esercitazione si svolge lavorando sul quadro di rappresentazione; la fase che segue si dedica,
invece, al mirino (cioè al Punto di Vista); così come è stato fatto per i Punti di
Fuga, anche il Punto di Vista viene proiettato sul banco; nel caso specifico è assai
semplice individuarlo poichè coincide esattamente con il centro del cerchio della
base del cilindro. Ottenute le tre proiezioni sul banco si fa unire, graficamente,
il punto di vista ai due punti di fuga. L'esercitazione è giunta quasi al termine:
l'ultima osservazione, quella essenziale, è che i due segmenti tracciati sono tra loro
ortogonali (come il pavimento) e che mantengono un rigoroso parallelismo con i
rispettivi giunti della pavimentazione.
La visione prospettica col metodo dei punti di fuga
Dopo aver svolto l'esercitazione con il prospettografo, e presentandone la
restituzione grafica su foglio, bisogna che l'impianto dell'esercitazione sia ancora
allestito e ben visibile. Nel "trasferimento" dell'immagine si dovrà dapprima
rappresentare il Piano orizzontale: qui si riconoscerà il Quadro (in scorcio totale),
la pavimentazione ortogonale (ed obliqua rispetto al quadro, il Punto di Vista.
Poi procedendo a ritroso rispetto all'esercitazione col prospettografo, si chiede
agli allievi di individuare i due punti di fuga, cercando di rispettare il vincolo
essenziale osservato nell'esercitazione: due rette che hanno origine dal punto di
vista rigorosamente parallele ai giunti della pavimentazione. Gli estremi della
nuova prospettività sono conclusi. Nella parte superiore dell'esercizio si prepara
l'immagine del quadro di rappresentazione: linea di terra, orizzonte; poi in
proiezione (ed a ritroso) si individuano i punti di fuga finali (all'altezza
dell'orizzonte), mentre all'altezza della linea di terra si proietteranno tutte le
tracce dei giunti del pavimento all'intersezione col quadro. la prospettiva si
conclude unendo le tracce sulla linea di terra con i punti di fuga.
Compresa pienamente la stretta connessione tra giunti del pavimento e rette di
individuazione dei punti di fuga, le rappresentazioni possono proseguire con i
pavimenti più diversi.
Per rafforzare il legame tra le due prospettive (metodo dei raggi visuali e
dei punti di fuga) è utile recuperare la prima prospettiva (quella realizzata col
metodo dei raggi visuali), poggiarvi sopra un foglio di carta trasparente e, prendendo
in considerazione dapprima il solo Piano Verticale (quello col quadro prospettico in
vera grandezza), riprodurre la figura in prospettiva; quindi (magari cambiando il
colore) prolungare gli spigoli della figura per confermare anche in questa circostanza
l' incidenza delle rette in due punti di fuga e da questi produrre l'orizzonte
geometrico (riconfermandone l'altezza con il Punto di Vista). Per i prolungamenti
degli spigoli sulla linea di terra occorre fare un importante distinguo poichè alcune
rette poggiano sul piano orizzontale altre no. Le rette appartenenti al piano
orizzontale individuano immediatamente le tracce, quelle sospese sono utilissime
per descrivere l'altezza della figura, grazie agli alberi delle altezze;
infatti tra questi e l'altezza della proiezione della figura sul piano verticale
dovrà esserci perfetta corrispondenza.
L'elaborato prodotto dovrebbe essere sufficiente a mostrare la stretta
connessione tra le due prospettive, per chi volesse ulteriore conferma, si potrebbe
proseguire anche con la rappresentazione del piano orizzontale: il punto di vista, il
quadro e le proiezioni della figura (ed il prolungamento degli spigoli sino sul
quadro) nonchè la proiezione dei punti di fuga precedentemente individuati; l'immagine
prodotta consente di confermare, ancora, l'esatto parallelismo tra le rette dei punti
di fuga (originate dal punto di vista), ed il prolungamento degli spigoli della figura.
Osservazioni a latere delle esercitazioni
Procedendo nelle attività di rappresentazione con il prospettografo si noterà
che finchè tali rappresentazioni restano in un'area della superficie trasparente
circostante la perpendicolare tra il mirino (punto di vista) ed il quadro stesso,
il rappresentato è visibilmente soddisfacente. Altrettanto si noterà che più ci
si allontana da questo punto (che è poi il punto principale, o centrico), il rappresentato tende
a deformarsi, l'immagine "forza".
Questa deformazione non incide sulle procedure descritte, per cui prolungamenti,
estensioni, ricerca dei punti di fuga e delle tracce, mantengono inalterate le proprietà
geometriche. Questa forzatura è provocata dalle modalità d'uso di questo prospettografo:
osservare nel mirino e contemporaneamente tracciare sul quadro trasparente l'immagine
prospettica obbliga a mantenere, tra questi, una distanza contenuta (la lunghezza del
braccio). Le deformazioni diminuiscono, confermate dai commenti già riportati nella
sezione "Vetri, finestre, reticoli e coordinate", con l'aumentare della
distanza tra il quadro ed il mirino.
Questi ambiti possono venire introdotti nelle lezioni quando, oramai
Sia ben compresa la modalità dell'esecuzione della prospettiva, di fronte alla
insoddisfazione dell'immagine forzata, se ne può illustrare la soluzione possibile.
Per pratica assodata (quasi una convenzione oramai nei valori numerici) si
considerano visibilmente soddisfacenti le immagini che rientrano nel cosiddetto
Cono Ottico. Questa area è chiaramente visibile pensando ad un cono posizionato
con il vertice coincidente con il mirino, l'asse perpendicolare al quadro trasparente
e la generatrice obliqua di 30° rispetto all'asse; il cerchio di intersezione tra
questi ed il cono è l'area in questione. Una interessante discussione su questo problema ha opposto,
nel Rinascimeto, le opinioni di Piero della Francesca
espresse esplicitamente nel teorema 12 del secondo libro, con quelle di leonardo da Vinci.
Ma cosa accade se il cono ottico, mantenendo la coincidenza del vertice col
mirino, si orienta in altra direzione perdendo l'ortogonalità dell'asse col quadro?
Di questo ambito ci occuperemo nella sezione successiva.
Il prospettografo e gli anamorfismi
Le rappresentazioni delle deformazioni prospettiche rientrano tra i così detti
anamorfismi. Per sintesi estrema si potrebbe dire che questo tipo di anamorfosi è la deformazione
estrema di una immagine (rappresentata sul foglio) ma che si "ricostruisce"
correttamente se osservata da un determinato punto di vista (quello del mirino).
Per realizzare una esercitazione con il prospettografo è sufficiente, dell'impianto
tipico sinora conosciuto, variare la posizione del quadro di rappresentazione;
dalla frontale rispetto al mirino, alla inclinata cercando un forte scorcio. Il
procedimento di rappresentazione dell'oggetto è sempre lo stesso (anche se stavolta
trovare i punti non sarà altrettanto comodo: causa i diversi allungamenti del braccio).
Il risultato finale è stupefacente, sul quadro di rappresentazione l'immagine è
talmente deformata che quasi non si legge più ma se a turno gli allievi traguardano
nel mirino riconfermano, invece, la leggibilità iniziale dell'immagine.
Un'altra esercitazione assai interessante legata all'anamorfismo è facilmente
presentabile agli allievi puntando l'attenzione sulla segnaletica stradale orizzontale,
quella dipinta sul manto stradale; gli esempi più evidenti sono quelli relativi alla
segnaletica sulle autostrade, quella che, in prossimità delle "uscite" avverte gli
automobilisti con il nome e la freccia. Se si presta attenzione a questa segnaletica
ci si accorge che le immagini dipinte sulla strada sono fortemente allungate (lungo
la direzione di marcia) leggibili solo se osservate di scorcio (il punto di vista del
guidatore).
Con il prospettografo (nella posizione regolare) si potrebbe ricreare la stessa
condizione, ma operando, con un altro tipo di proiezione: all'esatto contrario. Si
potrebbe preparare una scritta, ma anche una immagine (una freccia, una bicicletta
stilizzata) su un acetato da applicare direttamente sul quadro di rappresentazione;
quindi, con la collaborazione degli allievi, segnare, sul piano retrostante il quadro,
le proiezioni delle immagini intraguardate attraverso il mirino. Ci si accorgerà della
forte deformazione dell'immagine proiettata, dell'allungamento che ne deriva; le stesse
"forzature" realmente visibili sul manto stradale.
|
|