Gli albori della geometria proiettiva

4. Come rappresentare la profondità :
il  modo ottimo di Alberti

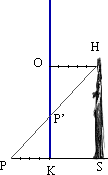
Come abbiamo visto le rette del piano orizzontale che si allontanano perpendicolaramente alla linea dove i due piani si intersecano, la così detta linea di terra, debbono disegnarsi sul quadro come segmenti che concorrono al punto centrico O.

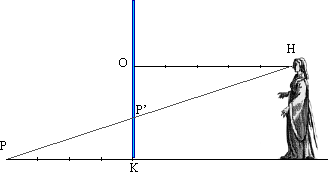
Muovendo materialmente col muose il punto P si può spostare la linea trasversa, parallela alla linea di terra e vedere dove va a proiettarsi sul quadro.

Vari metodi più o meno empirici, sono stato ideati dai pittori per trovare la giusta proporzione con la quale rimpicciolire le distanze per dare l’impressione della profondità. Ne citiamo uno, il   il metodo delle superbipartienti che è stato criticato da Alberti e che, pare, fosse ampiamente utilizzato nel ’ 400. Di questo metodo, che consiste nel diminuire ogni volta di due terzi, la rappresentazione di una distanza unitaria man mano che ci si allontana dalla linea di terra, ne parleremo ampiamnete nei commenti al testo albertiano.

Leon Battista Alberti, per primo scrive,  ad uso dei pittori, in un opuscolo, il   De Pictura, dove espone un metodo corretto dal punto di vista prospettico e molto semplice da realizzare per rappresentare il giusto degradare delle linee trasverse man mano che si avvicinano all'orizzonte.

È evidente che se un punto P ha la distanza PK dalla linea di terra (diciamo 4 braccia per fissare le idee), e se l’occhio è alla distanza OH dal quadro (diciamo 5 braccia), allora proiettando il punto P sul quadro otteniamo il punto P' che risolve il nostro problema. Basterebbe dunque riportare sul piano del quadro, con la stessa scala, la distanza dell’occhio e la distanza PK per poi proiettare e trovare la posizione della retta trasversa.

In questa figura abbiamo riportato la posizione nel quadro di una linea trasversa che dista 4 braccia dalla linea di terra vista dalla distanza di 5 braccia.

È evidente che questo metodo diventa molto scomodo, fino a diventare impreticabile, se la distanza dell’occhio diventa grande o se si devono disegnare delle linee trasverse molto lontane. La costruzione, insomma, per poter essere eseguita potrebbe richiedere molto spazio anche esterno allo spazio del dipinto, non sempre disponibile. Alberti suggerisce, in modo piuttosto oscuro per la verità, un nuovo metodo per ovviare a questa difficoltà, il modo ottimo non ben capito dalla critica anche recente. In questo CD presentiamo una nuova interpretazione, dovuta a Pietro Roccasecca, che interpreta, coerentemente con la lettera del testo, il metodo suggerito da Alberti.
L’osservazione cruciale implicita nel   modo ottimo è che, se si rimpicciolisce o si ingrandisce in proporzione la figura lungo la sola direzione orizzontale, lasciando inalterate le lunghezze nella direzione verticale, se si trasforma cioè il piano, come di direbbe oggi, con una affinità di centro K e autovalori w lungo la direzione orizzontale e 1 lungo la direzione verticale, allora la distanza KP' non cambia.

Questa osservazione che è facile dimostrare ¹ usando la teoria della similitudine, sicuramente notissima ai pittori, agli architetti, agli artigiani dell’ epoca, consente di sviluppare l'intera costruzione in un   piccolo spazio ad esempio sulla cornice del quadro.

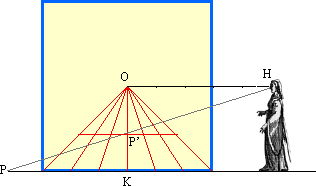
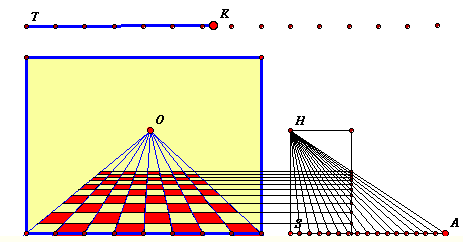
Nella animazione abbiamo ribaltato lungo la verticale la figura e abbiamo ripetuto la costruzione per differenti linee trasverse. La distanza TK rappresenta nella stessa scala del quadro, la distanza dell'occhio dal quadro. Il punto K può essere mosso modificando l'intera prospettiva. Questa distanza è stata riportata con una diversa scala sul segmento SA. Si vede quì chiaramente come spostando il punto A, la posizione delle linee trasverse non cambia, risultando la costruzione indipendente dalla scelta della lunghezza della linea SA. Notiamo che la costruzione albertiana permette di individuare in modo univoco la posizione dell'osservatore: il punto O (che dipende da due parametri) fissa la proiezione ortogonale dell'occhio sul quadro, mentre SK la sua distanza. L’efficacia del metodo di Alberti in questa animazione interattiva ci sembra si dimostri, nel senso di mostrare, in tutta la sua magnificenza. Dirà Alberti:

dimostrazioni quali, fatte da noi, gli amici, veggendole e maravigliandosi, chiamavano miracoli.

Possiamo spostare col mouse il punto O, alzandolo o abbassandolo dando in questo modo l'impressione, per chi osservi l'animazione, di essere in una realtà virtuale di volare sul pavimento. Possiamo anche, muovendo il punto K, simulare un movimento avanti e indietro come se camminassimo sul piano orizzontale.

Il segunente dipinto di Beato Angelico realizzato a metà del '400 segue molto da vicino le indicazioni di Alberti. Lo stesso Angelico aveva probabilmente conosciuto Alberti a Roma e sembra fosse a conoscenza del "modo ottimo". In questa Presentazione la linea centrica è tracciata all'altezza degli occhi dei personaggi e il degradare delle colonne, come risulta dalla nostra ricostruzione prospettica, sembra realizzata con le procedure albertiane.

Per verificare la correttezza prospettica del dipinto abbiamo tracciato un certo numero di segmenti orizzontali della stessa lunghezza (che può essere scelta arbitrariamente), li abbiamo congiunti con un punto all'altezza della linea dell'orizzonte e abbiamo cercato una linea verticale che riuscisse a traguardare i punti diagonali di tutte le linee trasverse su cui si appoggiano le colonne. Abbiamo visto che, dopo 5 tacche, la verticale aveva esattamente la proprietà richiesta. Cliccando sul dipinto, questa proprietà diventa manifesta. Ne possiamo dedurre che, l'impianto della pittura è costruito considerando il punto centrico a una altezza di tre braccioa sulla linea di terra (perché i personaggi raffigurati sono alti tre braccia, stanno in piedi sul pavimento orizzontale e hanno gli occhi in corrispondenza alla linea di terra). In più, possiamo dire che la distanza dell'occhio dal quadro è 5 volte la distanza tra due colonne consecutive. Lo stesso quadro è stato analizzato da un'altro punto di vista nella scheda Immagini della geometria proiettiva

Proponiamo ora vari esercizi nei quali si propone di analizzare, come in questo caso, l'impianto prospettico di alcuni dipinti sulla base del "modo ottimo" di Alberti.

La costruzione di Alberti permette, insomma, di poter scegliere per via teorica e non più empirica, la posizione dell'osservatore e per ogni posizione mostrare graficamente il risultato della visione che ne consegue. Questo permetterà di progettare situazioni nuove città ideali dove la perfetta prospettiva darà l’illusione di "esserci dentro".

Terminiamo questo parargrafo con una animazione in formato QuickTime che riassume passo a passo la costruzione albertiana.