Scheda Didattica

Scheda didattica

Laura Catastini

Teorema 4

	Tra intervalli uguali e giacenti sullo stesso segmento rettilineo quelli visti da distanza più grande appaiono più piccoli.

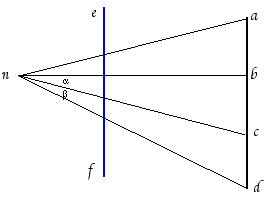
	I segmenti AB, BC e CD sono uguali e adiacenti sullo stesso segmento rettilineo. Si vuole dimostrare che se AB è più vicino all’occhio di BC allora è visto più grande, cioè che l’angolo AOB è più grande dell’angolo BOC. La stessa cosa vale BC e CD. Cosa debba intendersi per distanza di un punto da un segmento è chiarito in una apposita scheda dove sono presenti aspetti storici e didattici.
	Questo teorema, che può ovviamente essere generalizzato al caso di un numero qualunque segmenti uguali ed adiacenti, ha trovato varie applicazioni nell'antichità e nel rinascimento. Secondo Ovio ¹ le colonne romane, come ad esempio la colonna Traiana, venivano disegnate in modo che viste dal basso le figure in alto apparissero delle stesse dimensioni di quelle in basso. Il modo per realizzare questo effetto era quello di realizzare le figure più in alto più grandi di quelle più in basso, più vicine all'occhio dell'osservatore. Cliccando la colonna Traiana quì a fianco, appare il problema in una veste didattica. In Platone (Sofista,235E-236A) troviamo una testimonianza di questo modo di rappresentare le figure più lontane dal punto di vista: Coloro i quali eseguono qualche grande opera di scultura o pittura usano l'illusione. Infatti se riproducessero le reali proporzioni delle belle forme, le parti superiori, voi capite, sembrerebbero più piccole e quelle inferiori più grandi di quel che dovrebbero poiché le prime si vedono a distanza , le seconde a portata di mano... Cosí non è vero che gli artisti abbandonano il vero e danno alle loro figure non le proporzioni effettive ma quelle che sembrano essere belle?
	Anche Leonardo nel Libro di pittura si pone il problema di come realizzare grandi statue in modo che, viste dal basso sembrino proporzionate. In un passo aggiunge a proposito di come realizzare un ritratto: ² Prospettiva agiugne dove manca il giuditio nelle cose che diminuiscono; l’ochio non potrà mai essere vero giudice a determinare con verità quanto una quantità sia vicina ad un’altra simile, la quale altra sia colla sua sommità al pari dell’ochio riguardatore d’esse parti, se non per miezzo della pariete maestra e guida della prospettiva. Sia n l’ochio, ef la sopra detta periete a.b.c.d. siano le tre parti l’una sotto l’altra: se la linea an e cn sono lunghe a uno modo e l’ochio n si trova in mezzo, tanto parrà ab quanto bc, cd più bassa e più lontana da n : adunque parrà minore, e questo medesimo appare nelle tre porzioni del volto quando l’ochio del ritraente pittore è di pari altezza dell’ochio del ritratto. 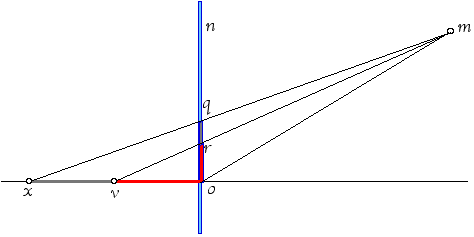Sulla pariete del quadro ef , i segmenti uguali ab, bc, cd si proiettano, per ragioni di similitudini, in segmenti uguali mentre l’angolo visivo b è più piccolo dell’angolo visivo a perché cd più bassa e più lontana da n come deriva dal teorema 4 che Leonardo mostra di conoscere. In un passo successivo, molto interessante Leonardo accogliendo criticamente le regole geometriche della prospettiva centrale, si rende conto delle aberrazioni che ne possono derivare quando l'occhio sia troppo vicino all'oggetto ³. L’ochio m vede li spazi o, v, x non conosce quasi differenza l’uno dall’altro e questo nasce per essere vicino a loro, e se li leverai detti spazi sulla pariete no , lo spazio ov apparirà nella parte della pariete or e così lo spazio vx apparirà in rq e se tu mettessi questo in opera in qualche loco che si potesse andare intorno ti parrebbe una cosa discordante per la gran varietà chè da lo spazio or e da rq e questo deriva che l’ochio è tanto sotto alla pariete che la pariete li scorta: onde se pure volessi metterlo in opera, ti bisognerebbe che essa prospettiva si vedesse da uno solo buso il quale fusse nel loco m o veramente stessi lontano almeno 3 volte la grandezza della cosa che vedi; la pariete op per essere sempre equidistante dall’ochio a uno modo renderà le cose bene e atte a essere vedute da loco a loco. 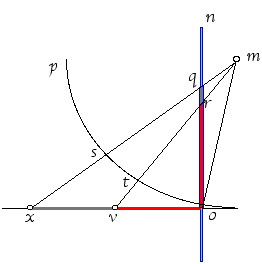In questo esempio l’occhio vede quasi uguali ov e vx , infatti sul cerchio op che è equidistante dall’occhio, gli archi ot e ts che corrispondono agli angoli visivi dei segmenti ov e vx , sono quasi uguali mentre sulla parete on sono presenti delle forti aberrazioni. I rimedi suggeriti da Leonardo sono due: 1) fissare in modo forzoso nel punto m l’occhio di chi guarda la prospettiva 2) allontanarela parete di almeno tre volte la grandezza dell’oggetto .

	Vediamo ora come possiamo dimostrare il teorema 4. L'argomento che troviamo nel testo euclideo si riferisce al caso speciale, più semplice, in cui l'angolo in A sia rettangolo, tuttavia la stessa dimostrazione può essere agevolmente estesa al caso generale usando le medesime idee del testo. Si traccia la parallela per B al raggio CO in modo da ritrovare i due angoli da confrontare all’interno dello stesso triangolo OBP.
	Nella figura animata se l’occhio è a sinistra dell'asse di AC allora sarà più vicino al segmento AB, altrimenti a BC per come abbiamo definito la distanza di un punto da un segmento.
	Supponiamo che l'occhio sia più vicino al segmento AB. Per dimostrare che l’angolo AOB è più grande dell’angolo BOC basterà dimostrare che il lato che sta di fronte a PBO, cioè OP, è più piccolo del lato che sta di fronte a BOP, cioè che OP < PB.
	Ma OP = PA perchè per ipotesi AB = BC e, i triangoli OAC e PBA sono simili avendo costruito la retta BP parallela al raggio OC. Dunque OP < PB se AP < PB.
	Per dimostrare che AP < PB consideriamo il triangolo PBA. PA è più piccolo di PB perché, per ipotesi, l’occhio O è più vicino al segmento AB che non a BC. Ciò significa che l’occhio si trova nel semipiano alla sinistra dell'asse di AC e quindi il punto P, che è il punto medio di OA, si trova alla sinistra dell'asse di AB, l’asse di AB, ( perché?) che è il luogo dei punti equidistanti da A e B. Dunque P è più vicino a A che non a B .
	È possibile dimostrare il teorema in altro modo, seguendo una via che non utilizza la teoria delle proporzioni ma alcune proprietà semplici del cerchio. Euclide stesso suggerisce questa prova nella dimostrazione del teorema 44. Se tracciamo la circonferenza che passa per i punti A,C ed O (per tre punti non allineati passa sempre una circonferenza), prolungando il raggio OB fino ad incontrare la circonferenza in P, vediamo che O è più vicino ad AB se e solo se P è a destra dell'asse di AC. Ma allora l'arco di circonferenza AP è maggiore dell'arco di circonferenza PC e quindi l'angolo AOP, che insiste su quell'arco, è maggiore dell'angolo POC che insiste sull'arco minore. Osserviamo che questo teorema si trova espresso essenzialmente nella stessa forma nel De prospectiva pingendi di Piero della Francesca Libro I, teorema 7. E' curioso il fatto che Piero, che sicuramente ha letto l'Ottica di Euclide perché la cita più avanti, proponga una dimostrazione, che forse riteneva più facile, diversa da quella di Euclide, ma sbagliata. Infatti la dimostrazione di Piero poggia su un assunto, forse un luogo comune ai suoi tempi, non sempre vero. Crediamo che, da un punto di vista didattico, sia molto utile far riflettere sugli errori sopratutto quando questi hanno un'origine tanto illustre. Una trattazione dettagliata di questo tema si trova in questo CD nella scheda didattica relativa al teorema 7 di Piero. L'esercizio sulla colonna Traiana usa la TAVOLA DELLE TANGENTI.